论文上对GPU的讨论之《基于图形处理器(GPU)的通用计算》
1.本文关注的是如何利用GPU实现矢量,矩阵的基本代数运算,然后在此基础上实现复杂运算(如线性方程组求解)。
2.图形硬件做通用计算主要目的是加速,来自其具备的以下主要优势:
一定的并行性:RGBA4颜色通道同时计算;一个时钟周期可以同时获得2个甚至多幅纹理。
高密集的运算:GPU内部存储器位宽大于CPU上的位宽,(GeForce FX 256位),适应传输大块数据。
减少了GPU与CPU的数据通:当整个应用针对图形生成的时候,不需要在CPU与GPU之间进行多次数据交换,GPU被认为是一个SIMD的并行机或者流处理器。CPU是个标量计算模型。
3.历史文献应用
【10,21,22,23,24】:利用像素程序求解一般代数问题,甚至偏微分方程(PDE),有限差分方程,及优化问题求解。
【18】:求解辐射度方程利用颜色来标记物体序号,利用深度缓冲来辅助计算物体可见性。
【25】:利用图形硬件进行实时的机器人运动规划,利用颜色标识障碍物多边形,然后将帧缓冲读回进行操作。
【26】:利用图形的多边形光栅化过程和深度缓冲检测来计算二维和三维通用Voronoi图,利用颜色标示每个位置,通过光栅化重构出距离函数;深度缓冲来进行距离比较,从而得到最近或者最远的位置。
光线跟踪:
【27】在像素级进行多余光线和一个三角形求交运算,其中,一幅纹理存放在各条光线起始点,另一幅纹理存放对应光线的方向,同时用三幅纹理来存放三角形,每次对一个三角形进行求交运算。
【28】将整个场景采用均匀网格表示,将所有三角形的顶点组织到三幅纹理中,并建立一个三角形链表纹理,这样可将整个光线跟踪算法放到GPU上来执行。
【29】针对辐射度,子表面散射光照模型采用GPU来加速计算,利用GPU雅可比迭代求解矩阵辐射度方程。对于子表面算法,利用顶点编程或者像素编程形成若干辐射图,最后用标准OpenGL绘制。
【30】进一步将整个辐射度的计算转移到GPU上去,能将量发射,可见性计算以及形状因子的计算全部放在GPU上完成,采用了建立纹理四叉树的策略对场景进行自适应细分。
【31】将Photon Mapping 方法移植到GPU,将photon存储在规则网格上,并给出两种实现思路:采用多遍技术对photon排序;利用顶点程序结合模板缓冲将photon排布到网格上,这些模板缓冲用来控制写入位置,从而采用宽度优先的随机光线跟踪求解出全局光照效果,其中排序、路由以及搜索运算都是基于GPU实现。
【32】将图像处理从时域转换到频域空间,利用GPU实现快速傅立叶变换,通过灵活组织避免重新排序(最终效果不如FFTW库)。
【33】利用GPU做三维卷积运。(利用了OpenGL1.2以上版本提供的颜色矩阵和卷积操作)
【34】利用GPU做小波变换。(利用了OpenGL1.2以上版本提供的颜色矩阵和卷积操作)
【35】利用硬件提供的颜色融合和OpenGL图像子集的卷积,颜色矩阵,计算折射,散射效果。
【36】利用图形硬件求解传热,各向异性扩散有限单元方程,实现图像处理的功能。
【37】利用有限元包分析出变形物体自振频率,然和采用模态分析的方法,利用顶点编程将物体各个振型进行叠加得到新位置,这样可将以前在CPU上进行的计算全部转移到GPU上去。
碰撞检测:
【38】采用两遍绘制方法,计算潜在的碰撞集合。(利用硬件遮挡查询操作来加速)
【39】采用多个GPU来加速可见性的计算。(利用硬件遮挡查询操作来加速)
【40】利用多纹理技术实现矩阵相乘。
【41】进一步对矩阵乘法做了优化。
【42】基于顶点编程开发了一个框架系统用来进行矢量运算,并在此基础上实现了矩阵乘法和3-SAT问题求解。
【10】利用像素程序来做基本的代数运算,然后在此基础上实现共轭梯度法、高斯-赛德尔迭代法,完成PEDs求解。
【21】基于像素编程的稀疏非结构化矩阵的共轭梯度法和正交网格的多重网格法,并用于加速几何处理和流体模拟。
【24】利用Direct X9下的HLSL实现稠密矩阵的系列代数运算,并在此基础上实现了共轭梯度法和线性优化问题求解。
【23】将最速下降法和共轭梯度法求解带有简单约束和规则化的非线性最小二乘优化问题映射到最新的图形硬件上,并将其应用到复杂的图像建模问题上。
【43】采用LBM(Lattice Boltzmann Method)模拟流体和烟的效果,将粒子包合成纹理,将Boltzmann方程映射到光栅化和帧缓冲操作上,整个计算是采用Register Combiner实现的。
【44】利用硬件计算LBM来模拟物体在风中飞舞的情形。
【20】通过Register Combiner编程求解CML(Coupled Map Lattice)问题,从而实现交互的对流模拟、反应扩散,以及沸腾效果模拟。
【45】【46】采用像素编程求解PDEs模拟云彩的运动。
【22】【47】实现了基于像素程序的多重网格算法,用来求解边值问题(传导问题,流体力学问题)。
【48】将冰晶体成长过程用GPU来实施物理计算,将整个物理方程组的计算在GPU上执行。
【49】【50】【51】将level-set等值面数据压缩为一个动态稀疏纹理格式,针对不同边界采用不同的像素程序来计算level-set的PEDs;另外,将一个活跃片段信息压缩成一个位矢量消息,从而将该消息传递给CPU以决定它需要传送给GPU的顶点和纹理坐标,这里还充分利用了赢家的自动Mipmapping技术进行低采样,以截止到一个像素。
【52】用来进行声音的合成运算,以使CPU和APU达到一个良好的均衡。
4.基于GPU的代数运算:
两种思路基于Register Combiner,基于像素程序。
4.1基于Register Combiner:
数据以顶点颜色的形式/纹理形式 传入Register Combiner,同时完成4颜色通道的计算。
4.2基于像素编程
像素程序可以访问独立的纹理,多达16个;
支持指令数目多达1024条;
寄存器个数多达64个。
比Register Combiner更具有可编程性,有更灵活的操作。
采用顶点编程【42】将矢量转换为一系列四元组,实现矢量,矩阵一些运算。但由于需要光栅化操作,将结果存在纹理或者帧缓冲中,然后读回到主存进行处理,如果数据量大,可能带来数据传输带宽瓶颈。
目前顶点编程支持分支,循环操作,但不能访问纹理,而硬件的像素处理能力比顶点处理能力高一个数量级,像素填充速度远比三角形传输速度高,且像素渲染管道比顶点渲染管道多,因此像素程序更适合用来做通用计算。
5.矢量与矢量的运算
用二维纹理来表示矢量;
纹理化的过程就是用一幅纹理来表示矢量的过程,矢量每个元素对应纹理每个纹元;
将纹理映射到一个与之匹配的矩形上,选取正投影模式,通过光栅化完成运算,输出结果为帧缓存或纹理;
6.稠密矩阵与矢量乘法运算
一般的矩阵与矢量运算,最直接方法采用纹元表示对应位置上的数据;
为了方便利用基本运算,采用4通道进行压缩表示;
采用对角线的方式来将矩阵划归为一系列的二维纹理,在像素程序中对因子矢量进行位置索引偏移,从而实现矩阵与矢量乘法【10】
7.稠密矩阵与稠密矩阵的运算
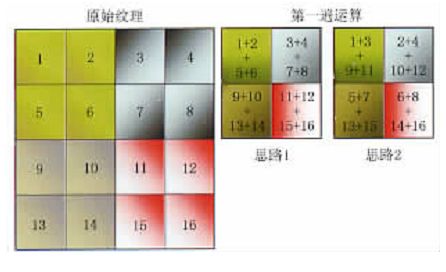
7.1把基本的4×1矩阵与矢量作为原子,把整个运算化解为若干原子操作,根据矩阵规模,硬件支持最大指令数目设定像素程序长度,从而采用多遍绘制思路来实现。【24】
7.2将矩阵单元表示为纹理颜色值,通过设置纹理坐标来进行行和列操作,将帧缓冲作为内存,利用多纹理和颜色融合技术实现矩阵与矩阵的乘法。【40】
7.3在7.2基础上通过对矩阵分块存储,以充分利用高速缓存的作用,并充分利用4个颜色通道进行并行运算,减少指令数目和需要处理的像素个数,还降低对带宽的要求。【41】
8.稀疏矩阵与矢量的乘法运算
8.1实际问题矩阵通常为稀疏的,如PDEs求解。
8.2根据矩阵信息生成顶点几何信息,顶点的坐标记录对应行号,颜色值为该元素的数据,对应纹理记录列号信息,然后光栅化得到结果,N遍绘制完成【10】
8.3【21】多纹理进行位置索引,减少稀疏矩阵0元素的存储:对角线元素存放纹理Aii,非对角线元素非0元素压缩存放在纹理Aij,每一行非对角线上第一个非0元素在上一个纹理中的位置存放到纹理R,对应矩阵中每一个非0元素矢量X分量位置同样存放到纹理C。(由于各行非0元素个数不同,每组具有相同个数非0元素的行都有一个像素程序与之对应)
8.4【13】将全部非0元素存放一幅纹理elem中,ipos记录非0元素的列号;start记录每一行第一个非0元素在纹理elem中位置,len记录每一行非0元素个数;整个运算共需6幅纹理,执行变数k次,k为各行最大非0元素个数。
8.5文章对以上两种方法提出了优化方法。
9.消减运算
定义:N维矢量(二维纹理)整理成一个标量。如求出矢量中的最大、最小元素、求矢量的某个范数。
【10】【21】介绍
10. 雅可比迭代法 略
11.共轭梯度法 : 文献【10】
12.PDEs求解 :文献【21,22,45,47】、【10】
参考文献