BP(Back Propagation)神经网络及Matlab矩阵实现
BP(Back Propagation)神经网络及Matlab矩阵实现
1、简介
人工神经网络是一种应用类似于大脑神经突触联接的结构进行信息处理的数学模型。在工程与学术界也常直接简称为“神经网络”或类神经网络。神经网络是一种运算模型,由大量的节点(或称“神经元”,或者“单元”)和之间相互联接构成。人工神经网络通常可以分为两类:依学习策略分类的网络(包含监督式学习网络(Supervised Learning Network)、无监督式学习网络(Unsupervised Learning Network)、混合式学习网络(Hybrid Learning Network)、联想式学习网络(Associate Learning Network)以及最适化学习网络(Optimization Application Network));依网络架构分类的网络(前向式架构(Feed Forward Network)、回馈式架构(Recurrent Network)以及强化式架构(Reinforcement Network))。
本文主要是对神经网络中的前向式网络进行Matlab实现(尽量使用矩阵操作)。
BP神经网络由以下的优点:
(1)、经证明可以实现任意复杂的非线性函数。
(2)、具有较强的学习能力以及一定的推广、概括能力。
(3)、实现简单,已应用于许多大型系统中。
在拥有以上优点的同时,BP神经网络仍有其缺点:
(1)、收敛速度较慢。
(2)、易于陷入局部极小,易出现过拟合现象。
(3)、网络结构的选择尚无完整的理论指导,一般只能由经验决定。
2、BP神经网络的相关矩阵推导
2.1、多层网络
假设网络具有M层(包含输入层),并使用0到M-1标记各层,则可以用下式来表示本网络:
![]()
![]()
其中![]() 表示由第m层神经元输出组成的矩阵,
表示由第m层神经元输出组成的矩阵,![]() 为第m及m+1层神经元之间的连接矩阵,
为第m及m+1层神经元之间的连接矩阵,![]() 是由第m+1层中神经元所对应偏移值组成的矩阵,
是由第m+1层中神经元所对应偏移值组成的矩阵,![]() 是由第m+1层中各神经元对应的激活函数组成的矩阵,
是由第m+1层中各神经元对应的激活函数组成的矩阵,![]() 表示第m层神经元的数目。由此可以看出,网络第零层为特征输入层(由P表示),第M层为最终输出层。
表示第m层神经元的数目。由此可以看出,网络第零层为特征输入层(由P表示),第M层为最终输出层。
![]()
![]()
2.2、性能指标
网络训练集由下式表示:
![]()
网络实际输出与期望输出的均方差可以表示为:
![]()
均方差的向量形式为:
![]()
单样本下,均方差的向量形式为:
![]()
网络的更新(使用最速下降法)可近似表示为:
其中α(alpha)表示网络的学习率。
2.3、规则链
样例:
![]()
![]()
![]()
将规则链应用到梯度计算可得:
2.4、梯度计算
第m层中第i个神经元的输出(未经过激励函数)为:
这里定义敏感度:
梯度:
2.5、最速下降操作
![]()
![]()
矩阵形式表示为:
![]()
![]()
2.6、雅克比矩阵
2.7、网络的反向传播(层间敏感度矩阵的推导)
![]()
首先计算网络末层的敏感度矩阵![]() ,然后可以反向计算各个前层的敏感度矩阵,直至网络第一层的敏感度矩阵(这里应该注意到:网络其实还包括第零层)。
,然后可以反向计算各个前层的敏感度矩阵,直至网络第一层的敏感度矩阵(这里应该注意到:网络其实还包括第零层)。
![]()
2.8、敏感度矩阵的初始化
![]()
![]()
2.9、网络训练算法简述
前向传播:
![]()
![]()
![]()
![]()
反向传播:
![]()
![]()
![]()
权值更新:
![]()
![]()
3、BP神经网络的Matlab矩阵实现
以下给出了一个按照本文第二部分所示公式编写的Matlab程序
%用最速下降法对网络权值的优化(这里的学习率是不变的) %本函数使用BP神经网络来对函数:y = 1 + sin((pi / 4) * ican * x)进行逼近,其中ican可以控制所逼近的 %函数的形状 clc; %清屏 close all; %关闭已打开的所有视图窗口 clear all; %清除工作空间中的所有变量 netInput = [-2 : 0.4 : 2]; %网络的训练样本 ican = 4; %控制网络所逼近的函数的形状 [featureNum , sampleNum] = size(netInput); %得到网络的输入特征数以及训练网络所用的样本数 inputNum = featureNum; %输入层的节点数(即输入的特征个数) middleNum = 3; %隐含层的节点数,这一层的激励函数选用Sigmoid函数 outputNum = 1; %输出层的节点数,这一层的激励函数选用线性函数 %初始化隐含层及输出层对应的权重和阈值矩阵 weight2 = rand(outputNum , middleNum) - 2 * rand(outputNum , middleNum); %初始化输出层对应的权重矩阵 weight1 = rand(middleNum , inputNum) - 2 * rand(middleNum , inputNum); %初始化隐含层对应的权重矩阵 threshold2 = rand(outputNum , 1) - 2 * rand(outputNum , 1); %初始化输出层对应的阈值矩阵 threshold1 = rand(middleNum , 1) - 2 * rand(middleNum , 1); %初始化隐含层对应的阈值矩阵 runCount = 0; %运行次数 sumMSE = 1; %训练样本的总均方差 minError = 1e-5; %网络可容忍的样本总均方差的最大值 assistS1 = zeros(middleNum , middleNum); %存储本文2.6部分中最后一个公式所得的变量,并辅助计算s1 assistS2 = zeros(outputNum , outputNum); %存储本文2.6部分中最后一个公式所得的变量,并辅助计算s2 afa = 0.1; %网络的学习率 %程序的主循环 while(runCount < 10000 & sumMSE > minError) sumMSE = 0; %每一次样本循环开始时,将样本的总均方差置为零 for i = 1 : sampleNum %根据每一个训练样本对网络进行更新 netMiddle = weight1 * netInput(: , i) + threshold1; %计算隐含层的输出 netMiddle = 1 ./ (1 + exp(-netMiddle)); %经过激励函数之后的隐含层的输出,隐含层的激励函数为logistic函数 netOutput = weight2 * netMiddle + threshold2; %计算网络前向传播中输出层的值 assistS1 = diag((1 - netMiddle) .* netMiddle); assistS2 = diag(ones(size(netOutput))); e = 1 + sin((pi / 4) * ican * netInput(: , i)) - netOutput; %计算网络期望输出与实际输出的误差 s2 = -2 * assistS2 * e; %s2的计算 s1 = assistS1 * weight2' * s2; %逆向计算s1 weight2 = weight2 - afa * s2 * netMiddle'; %更新输出层对应的权重矩阵 threshold2 = threshold2 - afa * s2; %更新输出层对应的阈值矩阵 weight1 = weight1 - afa * s1 * netInput(: , i)'; %更新隐含层对应的权重矩阵 threshold1 = threshold1 - afa * s1; %更新隐含层对应的阈值矩阵 sumMSE = sumMSE + e * e; end sumMSE = sqrt(sumMSE) / sampleNum; runCount = runCount + 1; end x = [-2 : 0.1 : 2]; y = zeros(size(x)); z = 1 + sin((pi / 4) * ican * x); %用训练后的网络绘制图像 for i = 1 : length(x) netMiddle = weight1 * x(: , i) + threshold1; netMiddle = 1 ./ (1 + exp(-netMiddle)); y(: , i) = weight2 * netMiddle + threshold2; end %训练的输出 plot(x , y , 'r'); hold on; %实际的输出 plot(x , z , 'g'); legend('网络实际的输出' , '网络期望的输出'); hold off;
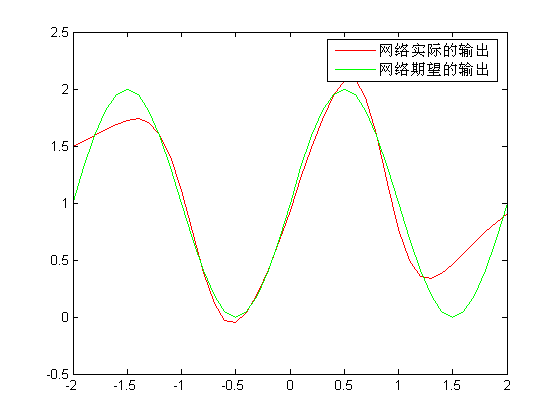
程序的输出图形如下:
为了使运行的结果更好,这里可以更改程序中的相关参数。由于网络的初始权重及阈值是随机的,因此得到的每一次程序结果图或多或少都会有一点不同。
4、参考内容
(1)、http://zh.wikipedia.org/wiki/%E4%BA%BA%E5%B7%A5%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C
(2)、http://blog.donews.com/elite/archive/2007/11/23/1230721.aspx
(3)、http://www.hudong.com/wiki/BP%E7%A5%9E%E7%BB%8F%E7%BD%91%E7%BB%9C
(4)、http://hagan.okstate.edu/nnd.html