一. 图模型(graphical model, GM)的表示
图模型(graphical model)是一类用图来表示概率分布的一类技术的总称。
它的主要优点是把概率分布中的条件独立用图的形式表达出来,从而可以把一个概率分布(特定的,和应用相关的)表示为很多因子的乘积,从而简化在边缘化一个概率分布的计算,这里的边缘化指的是给定n个变量的概率分布,求取其中m个变量的概率分布的计算(m<n)。
图模型主要有两大类,一类是贝叶斯网络(又称有向图模型);另外一类是马尔可夫网络(又称无向图模型)。
谈到一个图模型,主要有三个主要的关注点:
1)图模型的表示(representation); 指的是一个图模型应该是什么样子的
2)图模型的推断(inference); 指的是已知图模型的情况下,怎么去计算一个查询的概率,例如已经一些观察节点,去求其它未知节点的概率
3)图模型的学习(learning); 这里又分为两类,一类是图的结构学习;一类是图的参数学习。
在本文,我们主要关注图模型的表示,在以后的文章中,我们会论述图模型的其它方面。
一. 有向图模型的表示
顾名思义,有向图模型的结构表示是有向图的形式;通过一个有向图来表示一个概率分布,从而可以利用这个有向图模型来进行推断。
对于有向图模型,一个关键就是怎么通过一个有向图来表示一个概率分布呢?
对于一个概率分布p(x1,x2,...,xn),通过概率论中的链式法则,我们可以把它写成因子的形式
p(x1,x2,...,xn) = p(x1)p(x2|x1)P(x3|x1,x2)....p(xn|x1,x2....x_(n-1))
这是一个概率分布的一般形式,具体到一个特定的概率分布的时候,其中会有很多的随机变量是独立的或者条件独立的,从而可以
把上述式子进一步简化,例如x3, x1在给定x2的条件下是独立的,那么p(x3|x1,x2) = p(x3|x2)。在简化后的条件概率分布中,对于每个因子,我们这样来建立一个有向图,每个随机变量对应一个图的节点,然后对于每个因子,从它的条件部分的每个随机变量节点连一条边指向非条件变量节点,在完成所有的因子之后,就可以形成一个有向图模型。这样讲可能太抽象,下面我以一个具体例子来论述它的原理
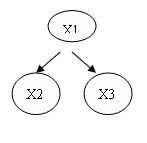
假设有这样一个概率分布p(x1,x2,x3) = p(x1)p(x2|x1)p(x3|x1)
那么它的有向图模型可以表示为
反之,给定一个有向图,我们可以从图直接写出这个图表示的概率分布,大家可以试着从上述图来写出它的概率分布。
形式化地,一个有向图模型表示的概率分布可以写为:P(X)= IIp(Xi|Pa(Xi)),其中X表示随机变量的向量,II表示乘积,Pa(Xi)表示Xi的父亲节点。
从上述描述可知, 要完整表示一个概率分布,一方面我们需要知道它的拓扑结构,即它的图形结构;
另外一方面,我们还需要知道概率分布的各个因子的分布情况,即上述公式中的P(Xi|Pa(Xi))需要知道。
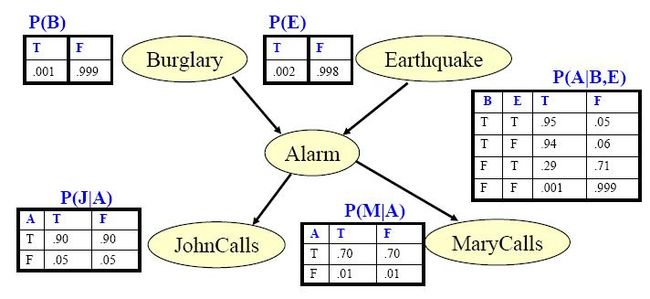
可以用另外一个图来表示一个完整的有向图模型的形式大概是什么样子
在上述图中的每个节点,都有一个条件概率分布表(CPT),这是有向图模型的参数,即P(Xi|Pa(Xi))。
二. 无向图模型的表示
无向图模型和有向图模型类似,都是为了表示一个概率分布,同时需要把变量之间的条件独立编码在图表示中,从而使得概率分布的表示可以被表示为因子乘积的形式,不同的是无向图模型是建立在无向图基础上,而有向图模型是建立在有向图基础之上。
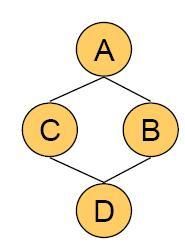
我们先看一个例子:
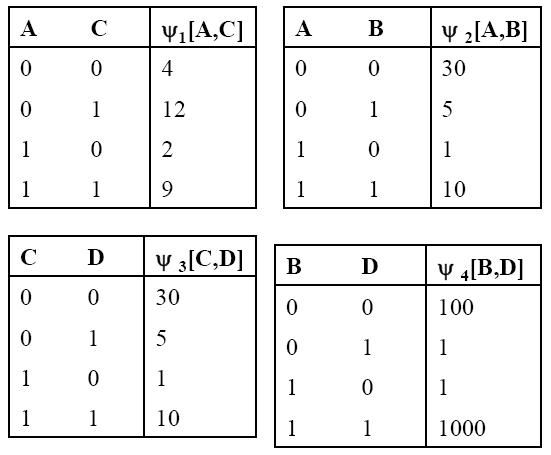
上图是一个无向图模型的完整的表示,左侧是它的拓扑结构,右侧是它的参数。
无向图模型是以最大团和定义在团上的势能函数(potential function)为核心,具体来说,在这个例子中,它有四个团,AC , AB, BD ,CD。那么我们需要在四个团上定义相应的势能函数,如右侧所示,必须注意势能函数必须为正。
最终这个无向图模型表示的概率分布是:P(A,B,C,D)= (1/Z)*/phi(A,C)*/phi(A,B)*/phi(C,D)*/phi(B,D)
其中,Z是归一化因子,因为势能函数并没有归一化,而要概率是[0,1],所以需要归一化;/phi 是表示相应的势能函数(这里因为不能表示数学符号,故而用了latex中的符号表示)。
所以一个无向图模型表示的概率分布形式化地可以表示为:
P(X)=(1/Z)*II_{i=1}^{n}/phi(Ci(x)),其中Ci表示的第i个团(都是利用了latex中符号表示数学公式。
三.小结
不管是有向图模型还是无向图模型,我们都需要关注它的两个方面,一方面是确定它的结构;一方面是确定它的参数,对于有向图模型,需要去确定它的条件概率表,对于无向图模型,需要确定每个团的势能函数。
因此,在下一篇博文中,我们将关注图模型的参数学习和结构学习。
2010-07-29 17:16:38