C语言实验：已知地球上两点的经度和纬度求其球面距离

要求：地球的平均半径为6371千米，已知地球上两个城市A、B的经度和纬度，编程序求出这两个城市之间的地面距离。

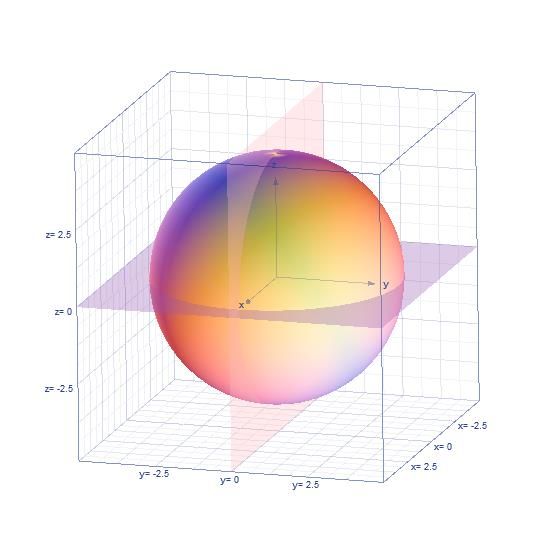
首先，固定两点，a(x1,y1,z1),b(x2,y2,z2)。

由空间解析几何及向量知识知：

其中，theta是两向量夹角，球面距离d：

对于A点来说，

theta就是A点的纬度值，即：

也即：

而对于A点的x，y坐标，首先：

r1是小圆的半径，也就是下图中的蓝色圆：

请注意平面图与立体图中坐标的对应，我已一一对应好，注意观察。

图中的alpha即：

所以，坐标与经度之间有如下关系：

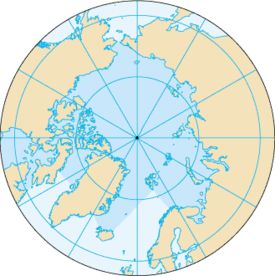
实际的北极点是这样的：

还有一点，东西经南北纬转化问题。

关于东西经和南北纬，在上面的阐述中，东经的点的y值都是正值，西经的点的y值都是负值，北纬的点的z值都是正值，南纬的点的z值都是负值。因为如下图，地球被分为了东北半球，东南半球，西北半球，西南半球：

如上分析，不难写出如下代码：

#include <iostream>
#include <cmath>
#include <string>
#include <cstring>
#include <cstdio>

using namespace std;

#define pi 3.1415926535
#define radio 6378137.0

//defining a new struct for the convenience of calculating
typedef struct
{
    long double Longitude;
    long double Lantitude;
    string East_or_West;
    string North_or_South;
} dot;
//function for calculating
int Distance(float lat1, float lon1, float lat2, float lon2)
{
    double latitude1,longitude1,latitude2,longitude2;
    double dlat,dlon;
    latitude1=lat1;
    longitude1=lon1;
    latitude2=lat2;
    longitude2=lon2;
    //computing procedure
    double a,c,distance;
    dlon =fabs((longitude2 - longitude1))*pi/180;
    dlat =fabs((latitude2 - latitude1))*pi/180;
    a = (sin(dlat/2)*sin(dlat/2)) + cos(latitude1*pi/180) * cos(latitude2*pi/180) * (sin(dlon/2)*sin(dlon/2));
    if(a==1.0)
        c=pi;
    else
        c = 2 * atan(sqrt(a)/sqrt(1-a));
    distance= radio*c;

    return distance;
}
int main()
{
    long double r = 6371.004;
    dot a, b;
    //freopen("D:\example.txt","r",stdin);
    while(1)
    {
        cout<<"Please input the two dots' coordinates like the following format: "<<endl;
        cout<<"East 30 North 20"<<"West 40 North 10"<<endl;
        //data input procedure
        cin>>a.East_or_West>>a.Longitude>>a.North_or_South>>a.Lantitude;
        cin>>b.East_or_West>>b.Longitude>>b.North_or_South>>b.Lantitude;
        //transfer
        {
            if(a.East_or_West == "East")
            {
                a.Longitude = a.Longitude;
            }
            else if(a.East_or_West == "West")
            {
                a.Longitude = - a.Longitude;
            }
        }
        {
            if(a.North_or_South == "North")
            {
                a.Lantitude = pi / 2 - a.Lantitude;
            }
            else if (a.North_or_South == "South")
            {
                a.Lantitude = pi / 2 + a.Lantitude;
            }
        }
        {
            if(b.East_or_West == "East")
            {
                b.Longitude = b.Longitude;
            }
            else if(a.East_or_West == "West")
            {
                b.Longitude = - b.Longitude;
            }
        }
        {
            if(a.North_or_South == "North")
            {
                b.Lantitude = pi / 2 - b.Lantitude;
            }
            else if (a.North_or_South == "South")
            {
                b.Lantitude = pi / 2 + b.Lantitude;
            }
        }
        //data output procedure
        float result = Distance(a.Lantitude, a.Longitude, b.Lantitude, b.Longitude);
        cout<<"The distance is: "<<result<<endl<<endl;
    }
}

可能有所纰漏，因为第一遍写代码的时候没这么仔细分析。

想要更深层次了解此问题，请参看微分几何中关于测地线及测地线曲率的相关问题。

欲证明该思想的正确性，可以采取如下反证法：

假设通过二点存在一个小圆对应的劣弧长比球面距离小，那条曲线未必是平面曲线，所以未必是圆弧。