KMP 算法（个人理解）

    KMP 算法听说很久了，去年吧，第一次听说 KMP 算法，后来决定学习 KMP 算法是在前天晚上，也就是 7 月 19 日晚上，准确说是在 7 月 20 日凌晨两点，抱着《算法导论》，翻到了《字符串匹配》这一章，想想，听说 KMP 很久了，要不就今天学学？然后就抱着书上床了，看了会，直接睡着了。。。第二天下午的组队赛中，尼玛，A 题就是赤果果的 KMP 啊，虽然他们说是什么 “扩展 KMP” ，但是会 KMP 的也能做啊！还好，昨天那题数据很水，我们队直接暴力过了，名次也上到了第三。晚上回到寝室终于不能再忍了，我要学 KMP！然后屁颠屁颠的百度去了，一来就找到了一片神贴！

    KMP 算法我是看的 matrix67 的文章学会的，这里是连接地址：KMP算法详解 BY matrix67

    相信大家看了 matrix67 的讲解，一定已经知道了 KMP 算法是怎么回事，怎么操作的，为什么时间复杂度不高

    这里，我主要是分享我对 KMP 的理解

   

KMP 的精髓是什么？

    这个东西，各自有个字的理解，很多人都觉得是避免了重复匹配，而我的理解是预处理

    为什么是预处理？

    你看看 KMP 的执行过程：

    假定现在我们有 A 串 ：abababacba 我们还有 B 串：babac

    进行匹配的时候：

             1 2 3 4 5 6 7 89 10

         A :a b a b a b a cb a

         B :b a b a c

    我们发现，现在 A B 串不能匹配，因为第一个字符就不相等，那么，我们怎么做呢？显然是进行下一次匹配嘛，我们把A 串的当前检查位子向前移一位，那么现在变成了：

             1 2 3 4 5 6 7 8 9 10

         A :a b a b a b a c b a

         B  :  b a b a c

现在，我们发现，A B 串对应的字符相等了，好了，那么接下来我们怎么做呢？当然是同时把 A B 串的检查位子向前移一位，来判断接下来的字符是不是相等，那么，我们有了下面的状态：

             1 2 3 4 5 6 7 8 9 10

         A :a b a b a b a c b a

         B :   b a b a c

咦，我们发现，他们还是匹配的，那么，接下来该怎么做呢？那就再把检查位子往前移，同时，我们也不难这样想，要是移到了B 或者 A 的最后一个字符了怎么办？这就简单了嘛，要是移动到了 B 串的最后一个位子，那么，我们肯定是找到了 B 在 A中的一个子串了。要是移动到了 A 串的最后一个位子，那么，我们已经把 A 串中所有位子找完了，接下来该怎么做呢？找完了就找完了啊，还能怎么做？好了，这些都是细节问题，我们先不谈，先看看接下来我们按照上面讲的操作，得到了什么样的状态：

             1 2 3 4 5 6 7 8 9 10

         A :a b a b a b a c b a

         B :   b a b a c

 

             1 2 3 4 5 6 7 8 9 10

         A :a b a b a b a c b a

         B :   b a b a c

 

              1 2 3 4 5 6 7 8 9 10

          A :a b a b a b a c b a

         B :    b a b a c

 

我们发现，现在 B 串和 A 串不能匹配了，这时该怎么办？

注意了，这就是普通匹配与 KMP 匹配的最大的不同，也是KMP 为什么高效的最重要原因。一般的，我们普通的匹配，要是遇到了这种情况，我们直接放弃了从 A 串的第 2 个位子开始匹配，转而以 A 串的第 3 个位子为起始检查位子，以B 串的第 1 个位子为起始检查位子，继续再和 B 串一个字符一个字符的匹配，直到匹配完成了为止。这些东西，我在没有学习KMP 之前就是这么干的，那么，传说中的 KMP 算法是怎么干的呢？

KMP 是这样干的，我们现在不是不能匹配了吗，我们把 B 串的检查位子后移，移到什么程度？假设移到了 pos 这个位子，那么，B 串中pos 这个位子一定要能够与 A 串中当前的检查位子相匹配。

好了，现在，我们来移动 B 串的当前检查位子：得到了下面的状态：

             1 2 3 4 5 6 7 8 9 10

         A :a b a b a b a c b a

         B :          b a b a c

好了，接下来，我们只要重复的进行上面的操作，就能够成功的在扫了一遍 A 串后，在 A 串中找到一个子串，它和 B 串匹配

但是，新的问题出来了，就是，当我们遇到 B串的当前检查位子和 A 串的当前检查位子不同的时候，我们不是要移动 B 串的检查位子吗？怎么移？一位一位的移？naïve！这样不就是退化成了普通的匹配了吗？那我们要怎么移动呢？

我们再来看看刚才这种状态：

             1 2 3 4 5 6 7 8 9 10

         A :a b a b a b a c b a

         B :   b a b a c

我们移动 B 串的检查位子到4，发现什么规律了吗？当然，这样多半不会发现什么规律，这样吧，我们做个约定，假设现在的检查位子在 5 ，我们判断下一个位子是否相匹配，相匹配的话，检查位子再向前移动一位，也就是说，在检查位子（包括检查位子）以前，A 串和 B 串是相互匹配的，那么，遇到上面这种情况，我们要移动 B 串的检查位子到 3

发现什么了吗？

B 串的前 k 个和后 k 个是匹配的！为什么？这就是a=b c=b 能够推出来 a=c 一样的。B 串的后 k 个能够和A 串当前检查位子的后k 个字符相匹配，而移动了 B 串的检查位子后，B串的前 k 个移动到了A 串检查位子的后k 个位子上，他们是匹配的，这样，B 串检查位子处的后 k 个字符和 B串的前 k 个字符相匹配就不难理解了。

问题就简化成了，我们要求出 B 串每个位子不能匹配的时候能够退到哪个位子？为了是算法的时间复杂度更高效，这个位子必须是距离当前不能匹配位子最近

注意这里：“B 串当前位子的前 k 个字符和后 k 个字符相匹配”，其实，这就转化成了B 串和自己匹配了。

我们设一个数组，记录每个位子能退到的最近的点，这里，一般我们字符串的开始位子是0，那么，next[0]=-1，这样就保证了极端情况

但是，我们的问题还是没有解决。怎么找出每个位子的前面的位子，也就是我们的 next[i]？

首先，我们在找 I 这个位子的时候，I 前面的位子的 next 肯定是已经找出来了，怎么利用前面的 next 来辅助我们找到现在这个位子的 next 呢？如果我们在注意观察，不难发现，假设现在我们要找的 next[i] ，那么，如果 B[next[i-1]+1]==B[i] ，那我们的 next[i] 肯定是等于 next[i-1] ，要是 B[next[i-1]]!=B[i] 呢？我们怎么处理？显然，这仍然和next[i-1] 有关，为什么？因为 i-1 之后是I ，就这么简单，既然 next[i-1] 不能满足条件，我们就看 next[i-1] 的 next 满不满足条件，即：B[next[next[i-1]]+1]==B[i] 吗？如果相等，我们找到了，如果不相等，那就继续找下一个 next ，直到相等，或者 next 指向了-1

那么，我们不难写出如下的代码：

是不是很精简？

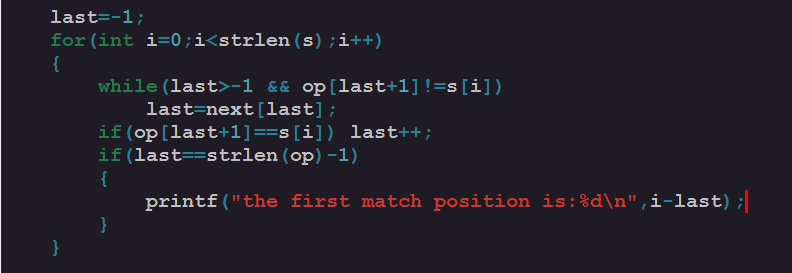
刚说了，找 B 串的next 其实就是一个 B 串自己与自己匹配的过程，这一过程读者一定要仔细理解，因为 KMP 的经典之处就在这里：先自己跟自己匹配，在和别人匹配。自己跟自己匹配是为了预处理，这样在和别人匹配的时候才能够高效的实现，下面，我们看看和别人匹配的代码：

好了，到这里，我们已经对 KMP 进行了一次分析，不难发现，真正的精髓就在自己和自己匹配找出 next 数组上了，下面献上完整的匹配过程代码：