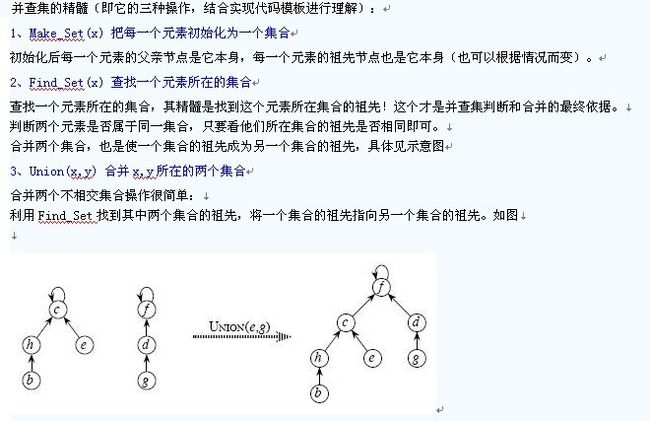
PKU 1161、PKU 2524、 PKU 1308

 

-----------------------------------例题一---------------------------------------
The Suspects
Time Limit: 1000MS		Memory Limit: 20000K
Total Submissions: 12013		Accepted: 5694
Description
Severe acute respiratory syndrome (SARS), an atypical pneumonia of unknown aetiology, was recognized as a global threat in mid-March 2003. To minimize transmission to others, the best strategy is to separate the suspects from others. 
In the Not-Spreading-Your-Sickness University (NSYSU), there are many student groups. Students in the same group intercommunicate with each other frequently, and a student may join several groups. To prevent the possible transmissions of SARS, the NSYSU collects the member lists of all student groups, and makes the following rule in their standard operation procedure (SOP). 
Once a member in a group is a suspect, all members in the group are suspects. 
However, they find that it is not easy to identify all the suspects when a student is recognized as a suspect. Your job is to write a program which finds all the suspects.
Input
The input file contains several cases. Each test case begins with two integers n and m in a line, where n is the number of students, and m is the number of groups. You may assume that 0 < n <= 30000 and 0 <= m <= 500. Every student is numbered by a unique integer between 0 and n−1, and initially student 0 is recognized as a suspect in all the cases. This line is followed by m member lists of the groups, one line per group. Each line begins with an integer k by itself representing the number of members in the group. Following the number of members, there are k integers representing the students in this group. All the integers in a line are separated by at least one space. 
A case with n = 0 and m = 0 indicates the end of the input, and need not be processed.
Output
For each case, output the number of suspects in one line.
Sample Input
100 4
2 1 2
5 10 13 11 12 14
2 0 1
2 99 2
200 2
1 5
5 1 2 3 4 5
1 0
0 0
Sample Output
4
1
1
Source
/* --------------代码------------*/
#include<iostream>
using namespace std;

int i, j, n, m;
int father[30005], num[30005];

void MakeSet( int n )
{
    for( i = 0; i < n; i ++ )
    {
        father[i] = i;
        num[i] = 1;
    }
}

int find( int x )
{
    if( x != father[x] )
        father[x] = find( father[x] );
    return father[x];
}

void Union( int a, int b )
{
    int x = find( a );
    int y = find( b );
    if( x == y )
        return;
    if( num[x] < num[y] )
    {
        father[x] = y; // y的子节点多，所以x的父节点归结于y；
        num[y] += num[x];
    }
    else
    {
        father[y] = x;
        num[x] += num[y];
    }
}

int main()
{
    while( cin >> n >> m && n )
    {
        MakeSet( n );
        for( i = 0; i < m; i ++ )
        {
            int count, first, b;
            cin >> count >> first;
            for( j = 1; j < count; j ++ )
            {
                cin >> b;
                Union( first, b );
            }
        }
        cout << num[find(0)] << endl;
    }
    return 0;
}
-----------------------------------------例题2-------------------------------------
Is It A Tree?
Time Limit: 1000MS		Memory Limit: 10000K
Total Submissions: 12034		Accepted: 4125
Description
A tree is a well-known data structure that is either empty (null, void, nothing) or is a set of one or more nodes connected by directed edges between nodes satisfying the following properties. 

There is exactly one node, called the root, to which no directed edges point. 
Every node except the root has exactly one edge pointing to it. 
There is a unique sequence of directed edges from the root to each node. 
For example, consider the illustrations below, in which nodes are represented by circles and edges are represented by lines with arrowheads. The first two of these are trees, but the last is not. 
 

In this problem you will be given several descriptions of collections of nodes connected by directed edges. For each of these you are to determine if the collection satisfies the definition of a tree or not. 
Input
The input will consist of a sequence of descriptions (test cases) followed by a pair of negative integers. Each test case will consist of a sequence of edge descriptions followed by a pair of zeroes Each edge description will consist of a pair of integers; the first integer identifies the node from which the edge begins, and the second integer identifies the node to which the edge is directed. Node numbers will always be greater than zero. 
Output
For each test case display the line "Case k is a tree." or the line "Case k is not a tree.", where k corresponds to the test case number (they are sequentially numbered starting with 1). 
Sample Input
6 8  5 3  5 2  6 4
5 6  0 0

8 1  7 3  6 2  8 9  7 5
7 4  7 8  7 6  0 0

3 8  6 8  6 4
5 3  5 6  5 2  0 0
-1 -1
Sample Output
Case 1 is a tree.
Case 2 is a tree.
Case 3 is not a tree.
Source
/*--------------代码----------------*/
#include<iostream>
using namespace std;
#define MAXN 10001
int f[MAXN], mark[MAXN], r[MAXN];

int find( int x )
{
    if( x != f[x] )
        f[x] = find( f[x] );
    return f[x];
}

int dec()
{
    int t, i;
    for( i = 1; i < MAXN; i ++ )
        if( mark[i])
            ++r[find(i)];
    t = 0;
    for( i = 1; i < MAXN; i ++ )
        if( r[i] > 1 )
            t ++;
    if( t > 1 )
        return 0;
    else
        return 1;
}
int main()
{
    int x, y, i, a, b, c = 0;
    while( 1 )
    {
        for( i = 1; i < MAXN; i ++ )
            f[i] = i, mark[i] = 0, r[i] = 0;
        int flag = 0;
        while ( cin >> a >> b )
        {
            if( ( a == 0 && b == 0) || a < 0 )
                break;
            x = find(a);
            y = find(b);
            mark[a] = mark[b] = 1;
            if( x == y || b != y )
                flag = 1;
            else f[b] = a;
        }
        if( a < 0 )
            break;
        if( flag )
            cout << "Case " << ++c << " is not a tree." << endl;
        else
        {
            if( dec() )
                cout << "Case " << ++c << " is a tree." << endl;
            else
                cout << "Case " << ++c << " is not a tree." << endl;
        }
    }
    return 0;
}
//------------------------ 例题3-----------------------------
Ubiquitous Religions
Time Limit: 5000MS		Memory Limit: 65536K
Total Submissions: 15006		Accepted: 7167
Description
There are so many different religions in the world today that it is difficult to keep track of them all. You are interested in finding out how many different religions students in your university believe in. 

You know that there are n students in your university (0 < n <= 50000). It is infeasible for you to ask every student their religious beliefs. Furthermore, many students are not comfortable expressing their beliefs. One way to avoid these problems is to ask m (0 <= m <= n(n-1)/2) pairs of students and ask them whether they believe in the same religion (e.g. they may know if they both attend the same church). From this data, you may not know what each person believes in, but you can get an idea of the upper bound of how many different religions can be possibly represented on campus. You may assume that each student subscribes to at most one religion. 
Input
The input consists of a number of cases. Each case starts with a line specifying the integers n and m. The next m lines each consists of two integers i and j, specifying that students i and j believe in the same religion. The students are numbered 1 to n. The end of input is specified by a line in which n = m = 0. 
Output
For each test case, print on a single line the case number (starting with 1) followed by the maximum number of different religions that the students in the university believe in.
Sample Input
10 9
1 2
1 3
1 4
1 5
1 6
1 7
1 8
1 9
1 10
10 4
2 3
4 5
4 8
5 8
0 0
Sample Output
Case 1: 1
Case 2: 7
Hint
Huge input, scanf is recommended.
Source
//---------------------代码----------------------------
#include<iostream>
using namespace std;

int n, m, maxNum, i;
int father[50005], num[50005];

void MakeSet( int n )
{
    for( i = 0; i < n; i ++ )
    {
        father[i] = i;
        num[i] = 1;
    }
}

int find( int x )
{
    if( x != father[x] )
        father[x] = find( father[x] );
    return father[x];
}

void Union( int a, int b )
{
    int x = find( a );
    int y = find( b );
    if( x == y )
        return ;
    if( num[x] < num[y] )
    {
        father[x] = y;
        num[y] += num[x];
        maxNum --;
    }
    else
    {
        father[y] = x;
        num[x] += num[y];
        maxNum --;
    }
}

int main()
{
    int Case = 1;
    while( cin >> n >> m && n || m )
    {
        maxNum = n;
        MakeSet( n );
        int a, b;
        for( i = 0; i < m ; i ++ )
            {
                cin >> a >> b;
                Union( a, b );
            }
        cout << "Case " << Case ++ << ": " << maxNum << endl;
    }
    return 0;
}