hdu1811Rank of Tetris--结题报告

题意很明了，但是我不知道是不是有人和我一样，一开始在纠结一个愚蠢的问题：

0 > 1, 0 > 2; 应该是能确定的，因为0 大于1,0大于2，那么1和2又可以按人品排名，应该是OK呀。。。。好吧，实在是智商捉急..答案是不确定的，因为按人品排名，我们只能是在 1 = 2 的情况下，没有说明 = ，那么怎么可以认为等级一样呢？

下面开始详细题解分析：

最开始做的时候，是在图论500题上看到的，分类是 拓扑+并查集，两个基本知识点都不难，我就上了。。谁知道。。。首先要想到，然后就是细心，我的处理方式是这样的：

1，先把等级一样的 ，也就是有‘=’ 的两个点并在一个并查集里面，也就是说，等级相同的，我们就看做一个点，用祖先root表示，其他的先不处理，用数组 a[i]  ch[i] b[i] 保存起来

2，然后我们再for(0 ~ M) 条边，遍历一次，用数组邻接表建有向图，记录入度，同时记录新图当中的点数node_num(这里等级相同的在一个集合里面看做一个点root)

3，然后就开始 拓扑排序，那么这里需要记录的情况比较杂乱，要细心

4，首先将入度为 0 的点入队，(这里用队列+邻接表来拓扑也是第一次，每次出队一个 u，我们对其进行拓扑，记录拓扑的点数 topo_num ++；然后用邻接表遍历邻接点  v--也就相当于删边操作，遍历过程中，邻接点 v 入度--，如果减完之后为0，那么入队，同时，记录一个节点删除会带来的入度为0的点数 num ++,如果num > 1,那么这里排名就不确定啦)，那么上面说的就是用队列+邻接表处理拓扑排序的一般方法，我们在这个题目中需要添加一点点东西，在对于出队的点，用邻接表遍历邻接点的时候，我们就把u 和 v 并在一个并查集里面，这里是为了后面判断拓扑完后，所有的点是不是在一个集合里面

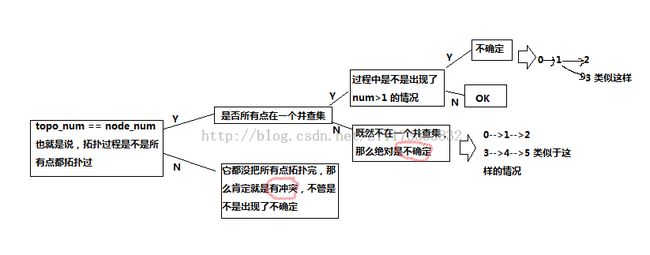
OK 基本的方法就在上面啦，那么这里主要情况比较复杂就在于什么时候我们是冲突，什么时候不确定，什么时候是OK，这里我这样判断的：

OK 上马：

#include <iostream>
#include <cstdio>
#include <queue>
#include <cstring>

using namespace std;

#define MAX 10005

int N,M;

int degree[MAX];//记录入度
int father[MAX];//并查集

struct Edge
{
    int to,next;
} edge[MAX*2];
int head[MAX],tol;

void add(int u,int v)
{
    edge[tol].to = v;
    edge[tol].next = head[u];
    head[u] = tol++;
}

int find(int x)
{
    if(x != father[x]){
        father[x] = find(father[x]);
    }
    return father[x];
}

char ch[MAX];
int a[MAX],b[MAX];
void initMap()
{
    for(int i = 0; i < N; i ++) father[i] = i;
    for(int i = 0; i < M; i ++)
    {
        scanf("%d %c %d",&a[i],&ch[i],&b[i]);
        if(ch[i] == '=') //同一级别的放在一个集合中
        {
            int x = find(a[i]);
            int y = find(b[i]);
            father[x] = find(y);
        }
    }
    //第二步来建图
    tol = 0;
    memset(head,-1,sizeof(head));
    memset(degree,0,sizeof(degree));
    for(int i = 0; i < M; i ++)
    {
        int x = find(a[i]),y = find(b[i]);
        if(ch[i] == '>'){
            add(x,y); degree[y] ++;
        }
        else if(ch[i] == '<'){
            add(y,x); degree[x] ++;
        }
    }
}

int topo()
{
    int node_num = 0;//新建图的点数
    queue<int>q;
    for(int i = 0; i < N; i ++)
    {
        if(father[i] == i){
            node_num ++;
            if(degree[i] == 0) q.push(i);
        }
    }

    int topo_num = 0;//经过topo的点数
    bool unsure = false;//是不是出现不确定情况
    while(!q.empty())
    {
        int num = 0;//这一轮过程中产生入度为0的点数
        int u = q.front();
        q.pop();
        topo_num++;
        for(int i = head[u]; i != -1; i = edge[i].next)
        {
            int v = edge[i].to;
            degree[v] --;
            father[find(u)] = find(v); //并入

            if(!degree[v]){
                num++; q.push(v);
            }
        }
        if(num > 1) unsure = true;//就已经说明不确定啦
    }

    bool inAset = true;
    for(int i = 0; i < N-1; i ++){
        if(find(i) != find(i+1)){ //两两之间在一个集合
            inAset = false;
        }
    }//下面的判断结合上图的分析
    if(topo_num != node_num) return 1;
    else{
        if(inAset){
            if(unsure) return 2;
            else return 0;
        }else return 2;
    }
}

int main()
{
    while(cin >> N >> M)
    {
        initMap();
        int ans = topo();
        if(ans == 1) cout<<"CONFLICT"<<endl;
        else if(ans == 2) cout << "UNCERTAIN" <<endl;
        else cout << "OK" <<endl;
    }
    return 0;
}

OK 个人愚昧观点，欢迎指正与讨论