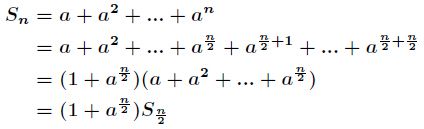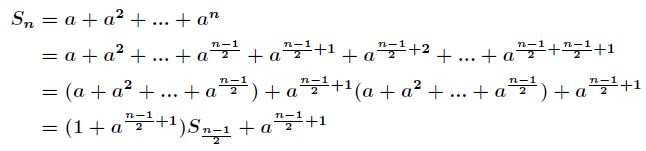等比数列二分求和

今天我们学习如何有效地求表达式的值。对于这个问题，用二分解决比较好。

 

（1）当时，

（2）当时，那么有

    

（3）当时，那么有

   

 

代码：

#include <iostream>
#include <string.h>
#include <stdio.h>

using namespace std;
const int M = 1000000007;
typedef long long LL;

LL power(LL a,LL b)
{
    LL ans = 1;
    a %= M;
    while(b)
    {
        if(b & 1)
        {
            ans = ans * a % M;
            b--;
        }
        b >>= 1;
        a = a * a % M;
    }
    return ans;
}

LL sum(LL a,LL n)
{
    if(n == 1) return a;
    LL t = sum(a,n/2);
    if(n & 1)
    {
        LL cur = power(a,n/2+1);
        t = (t + t * cur % M) % M;
        t = (t + cur) % M;
    }
    else
    {
        LL cur = power(a,n/2);
        t = (t + t * cur % M) % M;
    }
    return t;
}

int main()
{
    LL a,n;
    while(cin>>a>>n)
        cout<<sum(a,n)<<endl;
    return 0;
}

题目：http://poj.org/problem?id=3233

 

题意：矩阵求和

 

代码：

#include <iostream>
#include <string.h>
#include <stdio.h>

using namespace std;
const int N = 35;

struct Matrix
{
    int m[N][N];
};

Matrix I;
int n,k,M;

Matrix add(Matrix a,Matrix b)
{
    Matrix c;
    for(int i=0; i<n; i++)
    {
        for(int j=0; j<n; j++)
        {
            c.m[i][j] = a.m[i][j] + b.m[i][j];
            c.m[i][j] %= M;
        }
    }
    return c;
}

Matrix multi(Matrix a,Matrix b)
{
    Matrix c;
    for(int i=0; i<n; i++)
    {
        for(int j=0; j<n; j++)
        {
            c.m[i][j] = 0;
            for(int k=0; k<n; k++)
                c.m[i][j] += a.m[i][k] * b.m[k][j];
            c.m[i][j] %= M;
        }
    }
    return c;
}

Matrix power(Matrix A,int n)
{
    Matrix ans = I,p = A;
    while(n)
    {
        if(n & 1)
        {
            ans = multi(ans,p);
            n--;
        }
        n >>= 1;
        p = multi(p,p);
    }
    return ans;
}

Matrix sum(Matrix A,int k)
{
    if(k == 1) return A;
    Matrix t = sum(A,k/2);
    if(k & 1)
    {
        Matrix cur = power(A,k/2+1);
        t = add(t,multi(t,cur));
        t = add(t,cur);
    }
    else
    {
        Matrix cur = power(A,k/2);
        t = add(t,multi(t,cur));
    }
    return t;
}

int main()
{
    while(scanf("%d%d%d",&n,&k,&M)!=EOF)
    {
        Matrix A;
        for(int i=0; i<n; i++)
        {
            for(int j=0; j<n; j++)
            {
                scanf("%d",&A.m[i][j]);
                A.m[i][j] %= M;
                I.m[i][j] = (i==j);
            }
        }
        Matrix ans = sum(A,k);
        for(int i=0; i<n; i++)
        {
            for(int j=0; j<n; j++)
                printf("%d ",ans.m[i][j]);
            puts("");
        }
    }
    return 0;
}