图像处理(二十三)基于调色板的图像Recoloring-Siggraph 2015
基于调色板的图像Recoloring
原文地址:http://blog.csdn.net/hjimce/article/details/49226067
作者:hjimce
一、相关理论
最近刚搞完一个项目,难得有空闲的时间,于是打开了Siggraph 2015的网站论文,大体的扫描了今年的最新文献,在三维图形方面,CAGD向量场的相关文献,有好多篇paper,从这几年Siggraph文献看,向量场的分量加重了,这几年都有单独的向量场的模块标题,这下有的看了,还有三角网格曲面的参数化的相关paper也有好多篇。除此之外现在3D打印、VR也有了专门的标题了。
废话不多说,这里开始讲解2015 Siggraph的第一篇学习paper《Palette-based Photo Recoloring》,这篇文献可以说是一篇具有比较高的工程价值的paper,我们可以利用这个算法实现在ps、美图、天天p图等软件的一些相关功能,因为色彩变换应用场景很广,比如美白,我们希望只对肤色进行美白,而不是对整张图片进行变白。还有如果我们想要把唇色改变一下,都可以利用这个算法实现图片颜色调整颜色后的自然过渡。我觉得这篇文章最值得学习的地方是,就是图像局部颜色改变后的自然过渡实现。
OK,下面开始讲解paper的算法实现,这篇paper有很多的细节,有些细节可能讲的和paper有点区别、或者我忽略没细讲,因为讲的太细,要写好多页,打字打到累。
二、算法实现-2015 Siggraph:《Palette-based Photo Recoloring》
1、自动调色板颜色选择算法
这一部分,paper的创新点在如何对图像像素点进行快速聚类?
通过一种改进的k均值算法,进行聚类,paper默认选择k值为5,每个聚类中心颜色就是调色板颜色Ci。这个就像grab cut算法中,默认选择的图像颜色的聚类个数也是5。估计是5是一个比较好的经验值吧。然而paper说到,如果直接使用k均值算法,进行图像像素点的聚类,那么每次迭代计算,对于一个大的图片来说,很耗时间,这个我们可以想一下,如果一张彩色1000*1000的图片,如果直接使用k均值聚类,那么相当于对一百万个点进行聚类,这个计算量非常大,于是作者便提出了快速k均值图像聚类算法。那么作者是怎么进行快速k均值聚类的?
算法总流程:
(1)首先把图像的三个通道R\G\B归一化到[0,1]
(2)对每个通道进行直方图统计,直方图柱的个数选择bin=16。这样对于三通道图像来说,我们可以得到b*b*b个bins统计直方图柱
(3)这样对于每个bin,我们知道这个bin所包了图像的哪些像素点,我们选择计算其Lab空间的颜色均值作为聚类颜色中心ci(c是小写的)。因此我们可以得到16*16*16个ci
(4)接着paper直接对ci进行聚类。聚类方法是采用加权的k-means算法,权重的选择以每个bin所包含的像素点个数ni作为权值。
个人总结:上面的过程无非就是为了减少聚类点的个数,因为假设一幅图像是1000*1000的图片,那么点个数太多了,如果直接进行聚类,那很耗时。因此paper提出先使用直方图的方法,尽心预处理,把图像的n个像素点,减少为16*16*16个像素想,进行聚类,这样就可以大大减少时间了。这个就跟grab cut算法,进行预处理算法类似,可以大大提高grab cut算法的分割速度。
2、k-means算法优化部分
(1)准备知识
算法开始前,我先给大家讲个例子:假设有3000个不同的人脸,我要从中挑选出300个人脸,使得这300个人脸长相都最不相似。那么你要怎么做?或者在举个更简单的例子:有3000个二维的数据点,我要从中挑选300个数据点,使得这300个数据点之间两两之间的距离最大化,你要怎么做?。我想这个问题是构建机器学习算法训练数据库,经常遇到的问题了。
我的办法是最笨的办法,如果大家有更好的办法请不吝指导。我的方法:从3000个数据集A中随机挑选出一个数据点,作为第一个被我们挑选出来的点,加入B集合中(B就是我们要求的300个点),这样A中只剩下2999个点,B中有一个点。接着从A中剩下的2999个点中挑选,与B中的数据点距离最大的那个点,继续加入B中;如此循环迭代,直到B中有300个点为止。
OK,上面的例子就是接着作者的优化k均值算法的思想了。
(2)我们回到原paper的算法:
如果我们进行直接运用k-means算法,对16*16*16中颜色进行聚类,对于k均值聚类算法存在问题:首次迭代时,如果采用聚类中心随机初始化的方法,对于聚类结果的收敛性有很大的影响,这个只要学过k-means算法的人都知道。因此接着说下paper提出了k-means的初始化方法:
因为文献的聚类个数是5,也就是我们要从16*16*16个点中,挑选出5个聚类中心点,作为k均值的初始化中心点,我们希望挑选出来的这5个点都尽量的不相似。首先从ci中(ci表示上面的每个直方图的柱,也就是16*16*16个点,这里我把ci集合表示为A)选择包含的像素点ni个数最多的那个,作为第一个点,加入B中。然后从16*16*16-1个中挑选,与B中的点最不相似一个点,加入B中;如此循环迭代……。ci与cj的距离计算公式为:
![]()
其中参数σ作者默认的选择0.8,其实这个参数对结果影响不大,这个paper有提到,然后dij表示的是:ci与cj之间在Lab空间颜色值的距离,上面的计算是一个系数,最后要乘以剩余的每个类的n值。
个人总结:总之,我们就是要从16*16*16种颜色中,挑选出5种,使得这5种颜色最不一样,然后作为k均值聚类中心的初始化点。不说了,说多了都是泪,这么简单的算法,如果都看不懂,我只能给跪下了,打字打得好累。为了验证算法这一步写出来的代码,算法是否正确。我通过paper中的图片为例,这张图片我是通过paper的pdf版打开,然后选中文献中的实例图片,右键复制,然后保存下来的。
它的聚类结果如下,这是直接从文献上截下来的,它的聚类结果为图片下面的五个调色版颜色:
,因此我们写出来的算法,只需要验证这张图片,聚类后得到的5个聚类中心是否跟它一样就可以了,如果一样就代表自己写的代码,应该是没错,下面是我写的最后的聚类结果:
可以看到前面五个聚类中心刚好与paper显示的颜色一模一样,最后一个是黑色聚类中心,因为文献有讲到,它也是聚类6个类,其中一个类的颜色是黑色,在迭代过程中,这个中心点的位置不更新。然后聚类结束后,丢弃掉黑色这个类。
3、颜色转换定义
这一部分是paper的相关定义,也可以跳过不看,因为不涉及算法,主要是一些函数映射的定义。由前面的聚类过程,我们可以聚出了5个类,也就是5种颜色(k-means的聚类中心),这五种颜色将作为调色板,这个从下面的图就可以知道了,每张示例图的下面都有5个颜色:
当然也有可能一个图片就只有一两种颜色,比如下图,一张图片颜色较少,因此5个聚类中心距离较小的时候,我们可以把合并,这样下面的图片就只有三种调色板了。
我们定义5种调色板原来各自的颜色为Ci,经过用户调整后颜色变为Ci'。因此我们需要定义一个映射函数f,一个从Ci变换到Ci’相联系的函数。使得这个函数对于图片上的每个像素点的颜色x经过映射后的颜色为f(x),然后f(x)就是我们所要求经过颜色调整后每个像素点的颜色值。
OK,接着paper罗里吧嗦的就是为了讲关于映射函数f所需要具有的性质:
1、插值性质:对于原图片的每个像素点颜色值,如果它的值刚好为Ci,那么需要满足:
也就是说,如果图像上像素点的值刚好与五个调色板的某个颜色值Ci一样,那么我们肯定要让变换后的颜色值,就是Ci’,这个自己想想就应该是这样,无需废话。
2、值域性质:如果像素颜色值p的定义域为A,那么经过映射后f(p)也必须在A范围内。具体公式如下:
![]()
3、函数连续性,这个包含像素颜色连续性和调色板颜色连续性
4、一一对应关系。
如果:
那么:
5、亮度关系,也就是L通道的变换关系:
如果:
![]()
那么:
![]()
也就是说,如果原图像像素点p的亮度大于q的亮度,那么经过颜色调整后,满足p点的亮度还是大于q点的亮度。
个人总结:上面讲的都是废话,个人感觉很多文献就是喜欢这样,有的非常难的文献,看到定义看到想吐。接着三、四部分才是算法的重点,也是文献的最大创新点。可以认为这一部分作者是为了让自己的paper看起来更专业更牛逼一些,我们完全可以跳过不看。
三、亮度转换(L)
假设Li是调色板Ci的L通道值,为了简便起见,paper算法开始时,先根据L值得大小,对Ci进行排序。为我们
(1)根据上面的亮度性质关系,我们知道如果对于原始图像的5个调色板的L通道颜色值满足:
那么经过用户颜色调整后,五种聚类的L通道需要依旧满足:
![]()
上面这个式子,就相当于以一个约束条件,当用户在调整的时候,实时满足上面那个条件。那么它具体是怎么实现的呢?
根据上面的理论,当用户修改Ci’值的时候:
在这里需要非常明确:表示的是上次用户修改调色板j时的颜色,如果调色板j始终未被用户动过,那么的值就是初始化的时候Lj值,也就是:
![]()
在这里举个例子吧,因为这个估计会比较难理解。假设一开始调色板的颜色值,聚类成了10种,其颜色值分别为0、1、……、9,然后当用户调整3号调色板的时候,L3的值被用户修改成了7,那么其它的L值计算方法如下表:
| 初始Lj |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 用户修改 |
0 |
1 |
2 |
7 |
4 |
5 |
6 |
7 |
8 |
9 |
| 计算Lj’ |
min(0,1)=0 |
min(1,2)=1 |
min(2,7)=2 |
7 |
max(4,7)=7 |
max(5,7)=7 |
max(6,7)=7 |
max(7,7)=7 |
max(8,7)=8 |
max(9,7)=9 |
这样的操作,能保证调色板L通道升序排序,当j>i的时候;当j<i的时候,也可以保证L通道的降序排序。
同时这种策略,如果用户吧Li’提亮了,那么对于L’(j>i)也会跟着提亮,当用户把Li’调整到原始的值的时候,Lj’也会恢复到原始的值。看一下下面的表格,我们通过把3号调色板的颜色值,重新调整到值为3,那么其它调色板的L值得计算方法如表格所示:
| 初始Lj |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 当前值Lj’ |
0 |
1 |
2 |
7 |
7 |
7 |
7 |
7 |
8 |
9 |
| 3号调色板修改 |
0 |
1 |
2 |
3 |
7 |
7 |
7 |
7 |
8 |
9 |
| 重新计算Lj’ |
min(0,1)=0 |
min(1,2)=1 |
min(2,3)=2 |
3 |
max(4,3)=4 |
max(5,4)=5 |
max(6,5)=6 |
max(7,6)=7 |
max(8,7)=8 |
max(9,8)=9 |
可以看到,表格的第三行中,3号调色板被用户重新修改到值3的时候,其它的L值也会跟着恢复到原来的数值。上面计算方法中,需要注意的是,用户修改某个调色板I后,其它的调色板,需要以I为首元素,进行左右两个方向的递归,从而计算出其它调色板的颜色值。这样其实从上面的计算方法,你会发现,其实如果用户不改变最大最小值的调色板,那么其亮度范围是不会变化的,其依然是从0~9。这样也就满足了上面所说的性质2。
(2)另一方面,对于L通道的处理,上面讲的是Ci类的处理,这部分讲的是各个像素的处理。对于每个像素的亮度求取,定义一个变换函数:fL。这个函数定义了对于每个像素的新亮度值与调色板亮度值之间的函数关系。其实fL只用了两个相邻的palette entries进行加权组合,以此求解每个像素点的亮度值。
四、色彩转换(ab通道)
这一部分是文献的重点,也是paper的最大创新点。需要慢慢解读。前面我们已经定义了一个简单的亮度转换函数fL.也就是通过调色板的亮度,进行调色像素的亮度。本节引入lab函数用于颜色转换。
1、单一调色板
首先我们假设我们调色板就只有一种颜色C,也就是我们聚类的时候,只聚了一种颜色。我们以这种情况为特例进行讲解。假设当调色板的颜色从C调整为C’时,此时的颜色变换函数为f1。对于任意的一个颜色x我们希望求解:
![]()
正常的思维是,我们希望每个颜色x,变换后都具有相同的增量(C’-C)。
也就是说我们的一般思维是:
X’=X+C’-C
然而,这样的想法是不能满足上面的值域性质的,因为我们希望映射后,颜色范围依旧没有改变,如果简单的用这种方法,那么颜色就会很容易超出值域范围内了,于是呢作者就提出了一种方法,使得调整后的色域范围依旧不变的函数。
2、多调色板
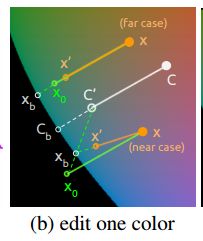
前面我们定义的是只有一种调色的情况,我们得到f1(x)函数,那么接着我们要结合实际,就是要有多种调色板的情况,也就是假设我们颜色聚类,聚了k种,paper默认选择k=5。对于有多个调色,文献直接采用一种颜色情况的加权组合,作为结果,这部分需要通过求解一个方程组,才能获得权重。其具体的示意图如下:
五、色彩转换结果
接着看一下我根据paper写出来的demo测试效果吧。首先先用paper上的一些图片示例作为测试,看看效果能不能达到和文章一样的效果再说:
测试示例1:
转换结果,上面我通过把衣服的色彩进行了转换,效果相当perfect。利用算法实现了上面衣服的颜色调整
测试结果2:
看出上面那副图的变换了吗?花蕊的中心变的更绿了,感觉过渡很自然,好开心,神器的算法
测试结果3:下面这幅图呢?看出变化了吗?地面的颜色、云朵的颜色都变成了绿色了。
接着在测试两张文献没有图片
测试结果4:
把跟地面相似的颜色变了一下,Perfect。
测试结果5:
上面的测试实例是通过把花草由绿色变为为另外一种颜色。
这篇文章后面还有很多细节,我没有具体的讲,需要自己慢慢细读paper,才能达到paper的效果,不然会出现过度不自然的现象,比如paper并不是对每个像素点进行recoloring计算,而是通过跟上面的k均值聚类的方法,进行bins颜色划分,然后对bins的每个节点进行recoloring,然后通过这些节点,对原始图片的像素点进行立方插值。
参考文献:
1、《Palette-based Photo Recoloring》
**********************作者:hjimce 时间:2015.10.10 联系QQ:1393852684 地址:http://blog.csdn.net/hjimce 原创文章,版权所有,转载请保留本行信息********************