算法入门3:分支算法(下)
分治算法的设计模式 - 大化小,小化了
分治算法的主要步骤就是:分解,求解,合并。
Divide-and-Conquer(P)
{
//问题规模足够小,直接解决
if(P≤n0) return(ADHOC(P);
//问题规模大,则分解为较小的子问题 P1 ,P2 ,...,Pk
divide p into smaller subinstance P1 ,P2 ,...,Pk
//递归解决每个小问题
for i = 1 to k
yi = Divide-and-Conquer(Pi)
//合并子问题的解
T = MERGE(y1,y2,...,yk)
return(T)
}
经典问题
(1)二分搜索
(2)大整数乘法
(3)Strassen矩阵乘法
(4)棋盘覆盖
(5)合并排序
(6)快速排序
(7)线性时间选择
(8)最接近点对问题
(9)循环赛日程表
二分搜索
问题:从一个已经排好序的序列中,查找某一个元素。
分析:假设序列数组为a,大小为n,从小到大的顺序排列。按照最基本的思路,那就是遍历一遍数组,时间复杂度为O(n)。如果n很大,效率显然不够高,因为没有把题目中“已经排好序” 的条件用上。既然是已经排好序,那么就可以进行折半查找(二分搜索)。方法如下:
1. 将数组从中间分成上下两半,如果中间的值刚好是要查找的元素,直接输出结果。
2. 如果中间的值比要查找的大,那么说明要查找的元素只可能出现在上半段,再对上半段进行二分搜索。
3. 如果中间的值比要查找的小,那么说明要查找的元素只可能出现在下半段,再对下半段进行二分搜索。
这就是分治算法最典型的例子。每次把规模为n的问题划分成n/2,继续划分成n/4,n/8… 直到足够小能直接解决。
代码:
/************************************************************************
* 名 称:BinarySearch.cpp
* 功 能:分治算法案例:二分查找
* 作 者:JarvisChu
* 时 间:2013-11-7
************************************************************************/
#include "stdio.h"
/*----------------------------------------------------------------------------------
* 功 能: 在大小为n的数组a中查找元素tag
* 参 数: a[] 要查找的数组,从小到大排列
n 数组大小
tag 待查找的元素
* 返 回: 找到则返回所在下标,否则返回-1
------------------------------------------------------------------------------------*/
int BinarySearch(int a[],int n,int tag)
{
int low = 0,high = n-1,mid = 0;
while(low<=high)
{
mid = (low+high)/2;
//正好是中间的元素
if(a[mid] == tag)
return mid;
//在上半段查找
if(a[mid]>tag)
{
high = mid-1;
}
//在下半段查找
else
{
low = mid+1;
}
}
return -1;
}
int main()
{
//Test
int a[10]={0,1,2,3,4,5,6,7,8,9};
printf("%d\n",BinarySearch(a,10,4));
printf("%d\n",BinarySearch(a,10,11));
return 0;
}
棋盘覆盖
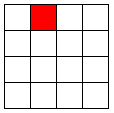
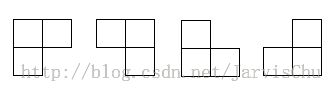
问题: 在一个2k×2k 个方格组成的棋盘中,恰有一个方格与其它方格不同,称该方格为一特殊方格,且称该棋盘为一特殊棋盘。在棋盘覆盖问题中,要用图示的4种不同形态的L型骨牌覆盖给定的特殊棋盘上除特殊方格以外的所有方格,且任何2个L型骨牌不得重叠覆盖。
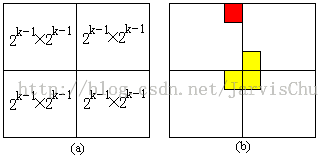
分析: 当k>0时,将2k×2k棋盘分割为4个2k-1×2k-1子棋盘(a)所示。
特殊方格必位于4个较小子棋盘之一中,其余3个子棋盘中无特殊方格。为了将这3个无特殊方格的子棋盘转化为特殊棋盘,可以用一个L型骨牌覆盖这3个较小棋盘的会合处,如 (b)所示,可以把黄色的方格看做是较小棋盘的特殊方格,从而将原问题转化为4个较小规模的棋盘覆盖问题。
递归地使用这种分割,直至棋盘简化为棋盘1×1。
代码:
/************************************************************************
* 名 称:Chessboard.cpp
* 功 能:分治算法案例:棋盘覆盖
* 作 者:JarvisChu
* 时 间:2013-11-7
************************************************************************/
#include <stdio.h>
/* L型骨牌的类型
------ ------| | |
| | | |
| | |------ ------|
*/
#define L1 1
#define L2 2
#define L3 3
#define L4 4
#define N 16 //棋盘大小,边长
int board[N][N]; //棋盘
/*----------------------------------------------------------------------------------
* 功 能: 对左上角为(tr,tc),边长为size的棋盘进行棋盘覆盖
* 参 数:(tr,tc)为棋盘的左上角坐标;(dr,dc)为特殊方格的位置;size为棋盘的大小,即边长
* 返 回:无
------------------------------------------------------------------------------------*/
void ChessBoard(int tr,int tc,int dr,int dc,int size)
{
//棋盘为1 x 1,不可再分割,直接返回
if(size == 1) return ;
//分割子棋盘
int s = size/2;//子棋盘大小
//判断特殊方格在哪个子棋盘内,以确定使用哪种L骨牌
int type = 0;
if(dr < tr+s && dc < tc+s)//特殊方格在左上角的子棋盘内
{
type = L4; //使用第四种类型的L骨牌
}
else if(dr < tr + s && dc >= tc + s) //在右上角
{
type = L3;
}
else if(dr >= tr + s && dc < tc + s) //在左下角
{
type = L2;
}
else //在右下角
{
type = L1;
}
//覆盖左上角的子棋盘
if(type == L4) //特殊方格在该子棋盘内
{
ChessBoard(tr,tc,dr,dc,s);//递归覆盖该子棋盘
}
else //特殊方格不在该子棋盘内
{
board[tr+s-1][tc+s-1] = type;//使用type型骨牌覆盖其右下角的方格
ChessBoard(tr,tc,tr+s-1,tc+s-1,s);
}
//覆盖右上角的子棋盘
if(type == L3) //特殊方格在该子棋盘内
{
ChessBoard(tr,tc+s,dr,dc,s);
}
else //特殊方格不在该子棋盘内
{
board[tr+s-1][tc+s] = type;//使用type型骨牌覆盖其左下角的方格
ChessBoard(tr,tc+s,tr+s-1,tc+s,s);
}
//覆盖左下角的子棋盘
if(type == L2) //特殊方格在该子棋盘内
{
ChessBoard(tr+s,tc,dr,dc,s);
}
else //特殊方格不在该子棋盘内
{
board[tr+s][tc+s-1] = type; //使用type型骨牌覆盖其右上角的方格
ChessBoard(tr+s,tc,tr+s,tc+s-1,s);
}
//覆盖右下角的子棋盘
if(type == L1) //特殊方格在该子棋盘内
{
ChessBoard(tr+s,tc+s,dr,dc,s);
}
else //特殊方格不在该子棋盘内
{
board[tr+s][tc+s] = type;//使用type型骨牌覆盖其左上角的方格
ChessBoard(tr+s,tc+s,tr+s,tc+s,s);
}
}
int main()
{
//初始化棋盘
for(int row=0;row<N;++row)
{
for(int col=0;col<N;++col)
board[row][col] = 0;
}
//设定特殊方格位置
int dr = 3,dc=4;
//棋盘覆盖
ChessBoard(0,0,dr,dc,N);
//打印棋盘
for(int row=0;row<N;++row)
{
for(int col=0;col<N;++col)
printf("%3d",board[row][col]);
printf("\n");
}
return 0;
}

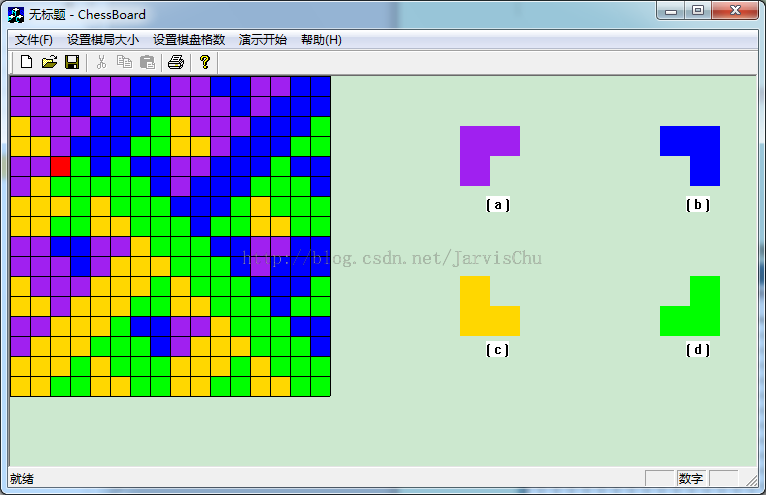
备注:博主用MFC实现了一个图形化的棋盘覆盖程序。如有兴趣可以留下邮箱索要源码。
可以设置棋盘的格数,特殊方格(红色)的位置,点击开始演示,则执行棋盘覆盖
转载本文请注明作者和出处
作者 :JarvisChu
出处:http://blog.csdn.net/jarvischu