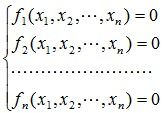0043算法笔记——【随机化算法】解非线性方程组

       问题描述

     求解下面的非线性方程组

    其中，x1,x2,…,xn是实变量，fi是未知量x1,x2,…,xn的非线性实函数。要求确定上述方程组在指定求根范围内的一组解。

    问题分析

     解决这类问题有多种数值方法，如：牛顿法、拟牛顿法、粒子群算法等。最常用的有线性化方法和求函数极小值方法。为了求解所给的非线性方程组，构造一目标函数

     式中，x=(x1,x2,……xn)。易知，上式取得极小值点即是所求非线性方程组的一组解。

    求解思路

    在指定求根区域D内，选定一个随机点x0作为随机搜索的出发点。在算法的搜索过程中，假设第j步随机搜索得到的随机搜索点为xj。在第j+1步，计算出下一步的随机搜索增量dxj。从当前点xj依dxj得到第j+1步的随机搜索点。当x<时，取为所求非线性方程组的近似解。否则进行下一步新的随机搜索过程。

    题外话：笔者在读王晓东《算法设计与分析》中这一节时，发现书上所给的代码似乎有些问题。在这里指出，如果提得不对，还请大侠们拍砖。书中给出的代码具体如下：

bool nonlinear(double *x0,double *dx0, double *x,double a0,
      double epsilon, double k,int n, int steps,int m)
{ 
    static randomnumber rad;
    bool success;
    double *dx, *r;
    dx=new double[n+1];
    r=new double[n+1];
    int mm=0;
    int j=0;
    double a=a0;
    for(int i=1;i<=n;i++)
    {
		x[i]=x0[i];
		dx[i]=dx0[i];
    }
    double fx=f(x,n);
    double min=fx;
    while ((min>epsilon)&&(j<steps))
    {
		if(fx<min)
		{
			min=fx;
			a*=k;
			success=true;
		 }
		else
		{
			mm++;
			if (mm>m)a/=k;
			success=false;
		}
		for(int i=1;i<=n;i++)
			r[i]=2.0*rnd.fRandom()-1;
		if(success)
			for(int i=1;i<n;i++)
				dx[i]=a*r[i];
		else 
		for (int i=1;i<n;i++)
			dx[i]=a*r[i]-dx[i];
		for (int i=1;i<n;i++)
			x[i]+=dx[i];
		fx=f(x,n);   
   }
   if(fx<=epsilon)
	   return ture;
   else
	   return false;
}

      问题1： while ((min>epsilon)&&(j<steps))句中，循环控制变量j<steps，但在循环体中，j没有自加，while循环永远不会结束。

     问题2：在循环体结束时，有赋值语句：fx=f(x,n);   笔者发现如果此时fx<epsilon时，程序while循环体会继续执行，到while开始几句是会更新min的值，可循环不会跳出，而会继续往下执行，更新数组x的值，重新计算目标函数f(x)。这样即时程序找到方程的解，也不会停下来。

    笔者纠正后具体程序如下：

//随机化算法 解线性方程组
#include "stdafx.h"
#include "RandomNumber.h"
#include <iostream>
using namespace std;

bool NonLinear(double *x0,double *dx0,double *x,double a0,
					double epsilon,double k,int n,int Steps,int M);
double f(double *x,int n);

int main()
{
	double  *x0,				//根初值
			*x,					//根
			*dx0,				//增量初值
			a0 = 0.0001,			//步长
			epsilon = 0.01,		//精度
			k = 1.1;			//步长变参
	int n = 2,					//方程个数
		Steps = 10000,			//执行次数
		M = 1000;				//失败次数

	x0 = new double[n+1];
	dx0 = new double[n+1];
	x = new double[n+1];

	//根初值
	x0[1] = 0.0;
	x0[2] = 0.0;

	//增量初值
	dx0[1] = 0.01;
	dx0[2] = 0.01;

	cout<<"原方程组为："<<endl;
	cout<<"x1-x2=1"<<endl;
	cout<<"x1+x2=3"<<endl;

	cout<<"此方程租的根为："<<endl;

	bool flag = NonLinear(x0,dx0,x,a0,epsilon,k,n,Steps,M);
	while(!flag)
	{		
		flag = NonLinear(x0,dx0,x,a0,epsilon,k,n,Steps,M);
	}	
	for(int i=1; i<=n; i++)
	{
		cout<<"x"<<i<<"="<<x[i]<<" ";
	}
	cout<<endl;

	return 0;
}

//解非线性方程组的随机化算法
bool NonLinear(double *x0,double *dx0,double *x,double a0,
					double epsilon,double k,int n,int Steps,int M)
{
	static RandomNumber rnd;
	bool success;			//搜索成功标志
	double *dx,*r;

	dx = new double[n+1];	//步进增量向量
	r = new double[n+1];	//搜索方向向量
	int mm = 0;				//当前搜索失败次数
	int j = 0;				//迭代次数
	double a = a0;			//步长因子

	for(int i=1; i<=n; i++)
	{
		x[i] = x0[i];
		dx[i] = dx0[i];
	}

	double fx = f(x,n);		//计算目标函数值
	double min = fx;		//当前最优值

	while(j<Steps)
	{
		//(1)计算随机搜索步长
		if(fx<min)//搜索成功
		{
			min = fx;
			a *= k;
			success = true;
		}
		else//搜索失败
		{
			mm++;
			if(mm>M)
			{
				a /= k;
			}
			success = false;
		}

		if(min<epsilon)
		{
			break;
		}

		//(2)计算随机搜索方向和增量
		for(int i=1; i<=n; i++)
		{
			r[i] = 2.0 * rnd.fRandom()-1;
		}

		if(success)
		{
			for(int i=1; i<=n; i++)
			{
				dx[i] = a * r[i];
			}
		}
		else
		{
			for(int i=1; i<=n; i++)
			{
				dx[i] = a * r[i] - dx[i];
			}
		}

		//(3)计算随机搜索点
		for(int i=1; i<=n; i++)
		{
			x[i] += dx[i];
		}

		//(4)计算目标函数值
		fx = f(x,n);
		j++;
	}	

	if(fx<=epsilon)
	{
		return true;
	}
	else
	{
		return false;
	}
}

double f(double *x,int n)
{
	return (x[1]-x[2]-1)*(x[1]-x[2]-1)
			+(x[1]+x[2]-3)*(x[1]+x[2]-3);
}

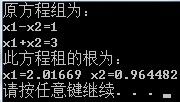
      程序运行结果如图：