局部敏感哈希(Locality Sensitive Hashing)
局部敏感哈希(Locality Sensitive Hashing)
计算item之间的相似项,计算item的top M最相似item,协同过滤计算(user based或item based)等等计算中,涉及大量两两相似项计算,计算复杂度为o(n2k),其中n为item量级,k为元素维度量级。即使hadoop和mpi使得模型可在多个机器或处理器协同计算,在处理o(n),nlog(n)复杂度问题时,如鱼得水。但是不说指数级的复杂度,对于m≥2的多项式级复杂度,都是一种对机器的亵渎,也成为了不是一般人或公司能玩得起的东东。
局部敏感哈希(Locality Sensitive Hashing, LSH)通过哈希方法,缩小两两相似(top)计算的范围,或缩小计算中item的维数,从而达到快速计算相似度的方法。使复杂度变为o(nml),其中n为item的量级,m<<n为新的搜索空间,类似于分支限界中的分支,l<<k,类似于降维处理。
由于笔者常关注于个性化推荐的top M服务,本文所述也主要用于此,但不限于此。
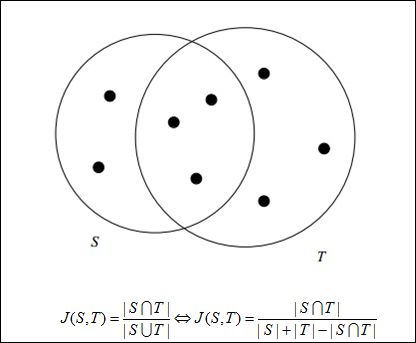
1 Jaccard相似度
Jaccard相似度计算十分便于计算离散集合之间的相似度,在个性化推荐中应用极广。Jaccard的相似度计算如图1所示,其中S和T的相似度为J(S,T)=3/8。
PS:大量连续的相似度计算,也可以转成Jaccard相似度计算,在此不述。
2 Simhash
Simhash主要做用是使复杂度o(nml)中,使m<<n,即大幅减小搜索空间的作用。例如计算item a的近临(top M)时,只搜索一个特定的近临空间m,而非整个庞大的n空间。
Simhash是通过设计一个hash方法,使要内容相近item生的hash签名也相近,hash签名的相近程度,也能反映出item间的相似程度。
Simhash算法如下:
假设item={item1,item2,…},取hash函数,将item的每一个元素hash成一个M位的int签名值,将int值按二进制表示,0处全表示为-1,记为H,将所有按位相加,最后加正的位为1,为负的位值为0,这就是item最后的simhash结果。这样就可以使相似的item有相近的hash值。
举例说明如下,假设item a ={1,2,3,4}, item b={1,2,3,5}, h(x)=x%8,M=3,有如图2中的结果,item a的sim hash值为(0,0,1,0),item b的sim hash值为(0,0,1,1),可见两者的sim hash值相似,通过两者的汉明码计算,便可以用汉明码来衡量两者的相似程度。
从降维的脚度看,通过将item预处理为simhash值后,通过计算两者的汉明距离计算相似度。可惜汉明距离并不能完全表征两者的实际相似程度,因而simhash常用于缩小搜索空间,计算item a的top M相似item时,搜索限为汉明距离最近的空间中。例如假设hash在64位,共将有264个hash桶,将所有item预先按hash桶建好索引后,计算item a的top M或满足某域值的相似item时,可从最近的hash桶中搜索,最近的桶为本桶中的其它item,其次为1位不同的其它hash桶,共64个,再次为2位不同的桶,共64*64个…
3 Minhash
Minhash主要做用是使复杂度o(nml)中,使l<<k,即减小计算两两相似度计算的维数。
由第1节可知,计算J(S,T)的关键在于计算S∩T或S∪T。直接求S∩T或S∪T,在有序的归并方法中,复杂度也是k的级别。Minhash的目的是降维,主要原理是两集合经随机转换后得到的两个最小hash值相等的概率等于两集合的Jaccard的相似度!(可以枚举出相应结果)。
由于只取一个hash函数时,只有相等与不等两个结果,对应于原理,也就只有相似与不相似不个结果。取一系列hash函数后,便可以概率性地统计出结果,而取hash函数的个数据,决定将k降维后的维数l,l越大,相似结果与实际相似度越相近,一般10个左右就已经能满足工程需求。
这样数据预处理完后,计算两item间的复杂度,就等于计算最小Minhash相同的概率了。
PS:在工程中,不容易找一系列的hash函数,由hash母函数生成的一系列hash函数可能相关,将降低Minhash的经度。
4 优势与局限性
Simhash和Minhash都有明显的应用局限性:
1、集合中的item要比较多;
2、所求的相关项要比较相似;
优势:
1、简化复杂相似项计算;
2、原理易于理解,点破后,给人显而易见的感觉。
参考:
Similarity estimation techniques from rounding algorithms;
Mining of Massive Datasets;
对于同仁们的布道授业,一并感谢。
----