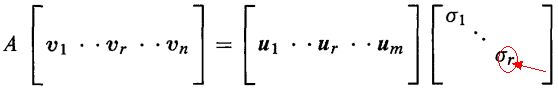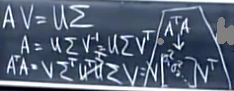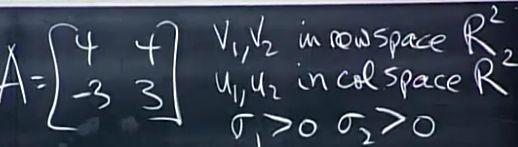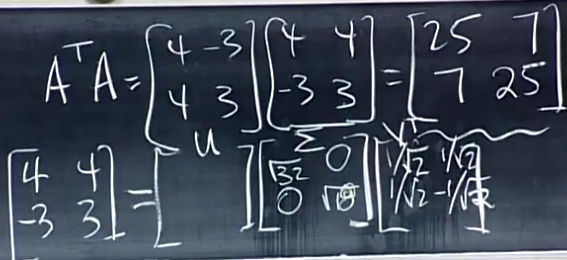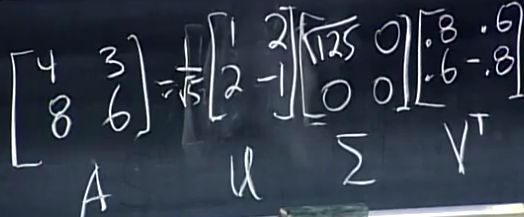线性代数导论30——奇异值分解
本文是Gilbert Strang的线性代数导论课程笔记。课程地址: http://v.163.com/special/opencourse/daishu.html
第三十课时:奇异值分解
本讲讲奇异值分解SVD=Singular Value Decomposition,这是矩阵最终和最好的分解。
任意矩阵A=UΣVT,分解的因子是正交矩阵,对角矩阵,正交矩阵。
正定矩阵的奇异值分解
A = SΛS-1= QΛQT,
正定矩阵由于其对称性,它们的特征向量是正交的,特征向量矩阵S可以改写为Q(A = SΛS
-1 是一般情况下的矩阵分解);
正定矩阵由于其正定性,一般的Λ矩阵成为正的Λ矩阵。正定矩阵的奇异值分解不需要两个U,V矩阵。
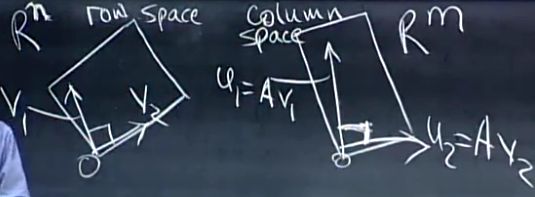
线性变换图解
A是m×n的矩阵,在行空间中找个典型变量,记为v1,然后变换到列空间的某向量,记为u1,有 u1=Av1。在奇异值分解中,要找的是行空间的一组正交基,然后变换成列空间的一组正交基。
那么这样的变换怎样合到一起,首先,这个行空间能找到一组正交基(格拉姆-施密特告诉我们以任意一组基开始,经过格拉姆-施密特正交化方法就可得到),但这组正交基经过A变换后不一定能在列空间成为正交基,所以行空间中的正交基要找特殊的。考虑零空间,这些零空间体现在对角矩阵Σ中是0。
Av变换过程中,我希望转换得到的正交单位向量,所以u1,u2..是单位正交基,同时v1,v2..也是单位正交基,Av1等于u1的一个倍数,即:σu1=Av1,σ称为伸缩因子。这种转换关系写成矩阵形式就是:
转化为:
AV=UΣ,(对于正定矩阵,这里是AQ=QΣ)
如果A存在零空间,那么行空间是r维,零空间是n-r维,我们同样可以取一组正交基。如果基零空间的向量为vr+1,...,vn,那么Avr+1将得到零向量,得到对角阵Σ对角线下方有一些0。
需要把整个Rn空间的标准正交基完善成整个Rm空间的标准正交基,
在对角阵Σ中用0来完善,所以存在零空间时没问题,
但行空间和列空间的基向量才是主要的。
同时,由AV=UΣ可得:A=UΣV
-1
=UΣV
T
。怎样找到V和U呢?
找V
:
ATA=VΣTUTUΣVT=VΣ2VT,得到的形式即:
ATA=QΛQT,因此ATA是一个正定矩阵,它的特征向量标准正交组成Q,特征值是σ2组成Λ。注意σ是Av=σu的伸缩因子,σ2是ATA的特征值。σ取σ2的正平方根。
找U
:
AAT=UΣVTVΣTUT=UΣ2UT,同样,形式即:
AAT =QΛQT,因此AAT是一个正定矩阵,它的特征向量标准正交组成Q,特征值是σ2组成Λ。注意σ是Av=σu的伸缩因子,σ2是AAT的特征值。
因此,
AAT和ATA是特征值相同,特征向量不同的相似矩阵。
奇异值分解:在线性代数的四个子空间中选出合适的基,v1到vr是行空间的标准正交基,用零空间的标准正交基vr+1到vn补充完整,u1到ur是列空间的标准正交基,用左零空间的标准正交基ur+1到um补充完整。A乘以每一个v对应一个u的方向,Avi=σiui,可将矩阵对角化A=UΣV-1=UΣVT
。
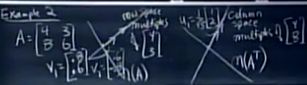
例子1:如下A矩阵,可逆,秩为2,需要在行空间R
2中找标准正交向量v1,v2,列空间R
2找标准正交向量u1,u2,系数缩放因子σ1>0, σ2>0,使的Av1=σ1u1,Av2=σ2u2。
A矩阵不是对称矩阵,它的特征向量不是正交的,所以所找的标准正交基不会是它们。分别计算A
TA,找到特征向量和特征值。并把特征向量标准化。这将得到V,得到V后利用使用AV=UΣ求解U。(视频中教授犯了一个小疏忽,教授不是通过AV=UΣ求解U,而是求解AA
T,取特征向量得到U,其实选择U的向量u的时候,要让其向量与Av的方向一致)
例子2:这时矩阵A2×2的秩为1,行空间是一维的,零空间是一维的,列空间也是一维的,左零空间也是一维的。行空间和零空间中可找出一组正交基转换到列空间和左零空间的一组正交基。