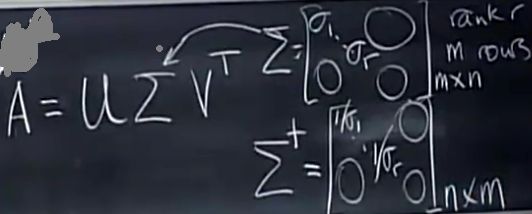线性代数导论34——左右逆和伪逆

本文是Gilbert Strang的线性代数导论课程笔记。课程地址： http://v.163.com/special/opencourse/daishu.html  

第三十四课时：左右逆和伪逆

本讲的主题是左右逆，伪逆，当然也包括以前的内容，四个基本子空间。

Am×n，m行n列

1）矩阵可逆：即两边逆，A A ^-1  = I =  A ^-1 A ， 此时r=m=n，A为方阵且满秩，零空间和左零空间都只有零向量。

2） 左逆：当列满秩，列向量线性无关，行向量不一定，r=n，零空间只有零向量，Ax=b存在0个或1个解。  A ^T A是n×n的对称矩阵，满秩， A ^T A是可逆的，称( A^TA)^-1A^T 为A的左逆，因为 ( A ^T A) ^-1 A ^T  *A=I。 这在最小二乘中至关重要，因为最小二乘以A^T A为系数矩阵（为什么统计学家喜欢这些？因为统计学家最喜欢用最小二乘 ），在列满秩的情况下， A ^T A可逆。此时[  ( A ^T A) ^-1 A ^T   ]为n×m，Am×n，得I为n×n。

3） 右逆：当行满秩，行向量线性无关，r=m， A ^T的零空间只含零向量，Ax=b有或无穷多个解，因为 A* A ^T ( A A ^T ) ^-1=I，所以 把 A^T(AA^T)^-1称为A的右逆。

4） 伪逆：r<m,r<n，行空间和列空间的维数相同，都是r维，行空间的任意向量x，与A相乘，得到恰好是列空间中的所有向量，行空间向量x与列空间向量Ax的关系是一 一对应的。所有向量都能由行空间的分量和零空间的分量构成， 行空间中向量x对应着列空间中的Ax（零空间中的x乘以A得零Ax=0），行空间中向量y对应着列空间中的Ay（如果x与y不同，那么Ax和Ay必然不同，证明：假设Ax=Ay, A(x-y)=0, 那么x-y属于零空间，那么x=y）。 但如果要从列空间得到行空间的向量呢，要得到行空间的向量，那么x=A⁺(Ax)，A⁺就是伪逆，伪逆把左零空间变为0，即如果A⁺乘以左零空间的向量，结果为0。（假设没有零空间的干扰，即假设零空间只有零向量，存在逆，那么行空间的向量x得到列空间的向量Ax，反过来，通过A的逆就能从列空间得到行空间， A^-1(Ax)=x。）

考察如上左逆中有：  (A^TA)^-1A^T *A=I，如果将左逆写在右边将得不到单位矩阵了，那么 A(A^TA)^-1A^T 是什么？

是在列空间投影的投影矩阵，它会尽量靠近单位矩阵，一个投影矩阵很想成为单位矩阵，但不可能做到。

右逆中， A* A ^T ( A A ^T ) ^-1=I，如果将右逆写在左边也不是单位矩阵了，那 A ^T ( A A ^T ) ^-1A是什么？

是在行空间投影的投影矩阵。

找伪逆 A ⁺

方法1：SVD，A= UΣV^T，对角阵Σ对角线上的元素为：σ1,σ2,...σr,0,0...，秩为r，那么Σ的伪逆是多少？

如果对角线上没有0元素，那么Σ是可逆的，ΣΣ ^-1=I，Σ ^-1中对角线元素为1/σ1,1/σ2,...1/σn。现在对角线上有0元素。

Σm×n和Σ⁺n×m都是秩为r的矩阵，伪逆是最接近逆的矩阵，那ΣΣ⁺对角阵m×m，对角线上方有r个1，下边为0。这是到列空间的投影矩阵。

那Σ⁺Σ将得到n×n的对角矩阵，是到行空间的投影矩阵。

那么 A的伪逆是多少？A⁺=VΣ⁺U^T，这就是最小二乘不适用的情况，当统计学家遇到非满秩的时候，SVD的奇妙之处就在于将所有问题都归到对角矩阵上。

以上就是 伪逆所做的事，乘在左边或右边得不到单位矩阵，得到的是投影矩阵。（乘在右边得到列空间的投影矩阵，乘在左边得到行空间的投影矩阵）