（第二周项目3）体验复杂度

(1)两种排序算法的运行时间

提供两种排序算法，复杂度为O(n 2  )的选择排序selectsort，和复杂度为O(nlogn) 的快速排序quicksort，在main函数中加入了对运行时间的统计。
利用一个将近10万条数据的文件作为输入数据运行程序，感受两种算法在运行时间上的差异。

运行中需要的数据文件

<1>复杂度为O(n 2  )

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#define MAXNUM 100000
void selectsort(int a[], int n)
{
        int i, j, k, tmp;
        for(i = 0; i < n-1; i++)
        {
                k = i;
                for(j = i+1; j < n; j++)
                {
                        if(a[j] < a[k])
                                k = j;
                }
                if(k != j)
                {
                        tmp = a[i];
                        a[i] = a[k];
                        a[k] = tmp;
                }
        }
}

int main()
{
    int x[MAXNUM];
    int n = 0;
    double t1,t2;
    FILE *fp;
    fp = fopen("numbers.txt", "r");
    while(fscanf(fp, "%d", &x[n])!=EOF)
        n++;
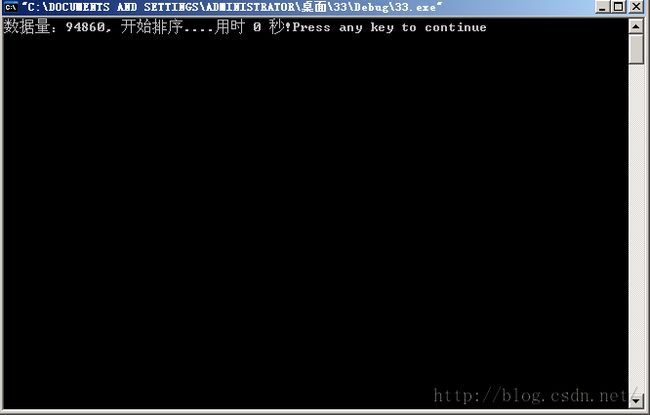
    printf("数据量：%d, 开始排序....", n);
    t1=time(0);
    selectsort(x, n);
    t2=time(0);
    printf("用时 %d 秒!", (int)(t2-t1));
    fclose(fp);
    return 0;
}

结果

<2>复杂度为O(nlogn)

#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#define MAXNUM 100000
void quicksort(int data[],int first,int last)
{
    int i, j, t, base;
    if (first>last)
        return;
    base=data[first]; 
    i=first;
    j=last;
    while(i!=j) 
    {
        while(data[j]>=base && i<j) 
            j--;
        while(data[i]<=base && i<j) 
            i++;
        /*交换两个数*/
        if(i<j)
        {
            t=data[i];
            data[i]=data[j];
            data[j]=t;
        }
    }
    data[first]=data[i]; 
    data[i]=base; 
    quicksort(data,first,i-1);
    quicksort(data,i+1,last); 
}

int main()
{
    int x[MAXNUM];
    int n = 0;
    double t1,t2;
    FILE *fp;
    fp = fopen("numbers.txt", "r");
    while(fscanf(fp, "%d", &x[n])!=EOF)
        n++;
    printf("数据量：%d, 开始排序....", n);
    t1=time(0);
    quicksort(x, 0, n-1);
    t2=time(0);
    printf("用时 %d 秒!", (int)(t2-t1));
    fclose(fp);
    return 0;
}

结果

（2）汉诺塔

用递归算法求解汉诺塔问题，其复杂度可以求得为O(2 n ) ，是指数级的算法。请到课程主页下载程序运行一下，体验盘子数discCount为4、8、16、20、24时在时间耗费上的差异，你能忍受多大的discCount。

#include <stdio.h>
#define discCount 4//替换8，16，20,24 
long move(int, char, char,char);
int main()
{
    long count;
    count=move(discCount,'A','B','C');
    printf("%d个盘子需要移动%ld次\n", discCount, count);
    return 0;
}

long move(int n, char A, char B,char C)
{
    long c1,c2;
    if(n==1)
        return 1;
    else
    {
        c1=move(n-1,A,C,B);
        c2=move(n-1,B,A,C);
        return c1+c2+1;
    }
}

结果

discCount=4

discCount=8

discCount=16

discCount=20

discCount=24

总结

复杂度不同，运行时间不在一个等级。n越大，部分数级改变明显。

心得

读取txt文件要将其与程序放在一个工程下。从define里改变量。