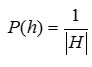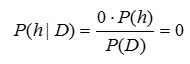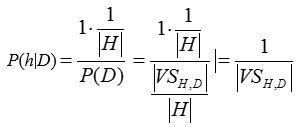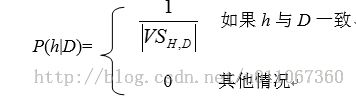贝叶斯学习--极大后验假设学习
我们假定学习器考虑的是定义在实例空间X上的有限的假设空间H,任务是学习某个目标概念c:X→{0,1}。如通常那样,假定给予学习器某训练样例序列〈〈x1,d1,〉…〈xm,dm〉〉,其中xi为X中的某实例,di为xi的目标函数值(即di=c(xi))。为简化讨论,假定实例序列〈x1…xm〉是固定不变的,因此训练数据D可被简单地写作目标函数值序列:D=〈d1…dm〉。
基于贝叶斯理论我们可以设计一个简单的算法输出最大后验假设
Brute-ForceMAP学习算法
1.对于H中每个假设h,计算后验概率:
2.输出有最高后验概率的假设hMAP:
此算法需要较大的计算量,因为它对H中每个假设都应用了贝叶斯公式以计算P(h|D)。
虽然对于大的假设空间这很不切实际,但该算法仍然值得关注,因为它提供了一个标准,以判断其他概念学习算法的性能。
下面为Brute-ForceMAP学习算法指定一学习问题,我们必须确定P(h)和P(D|h)分别应取何值(可以看出,P(D)的值会依这两者而定)。
我们可以以任意方法选择P(h)和P(D|h)的概率分布,以描述该学习任务的先验知识。但是先要满足下面的条件假设:
1.训练数据D是无噪声的(即di=c(xi));
2.目标概念c包含在假设空间H中;
3.没有任何理由认为某假设比其他的假设的可能性大。
一、如何确定P(h)的值
对H中任一h:
二、如何选择P(D|h)的值
换言之,给定假设h,数据D的概率在其与假设h一致时值为1,否则值为0。
接下来考虑该算法的第一步,使用贝叶斯公式计算每个假设h的后验概率P(h|D):
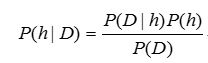
1、考虑h与训练数据D不一致的情形
2、考虑h与D一致的情况
VSH,D是H中与D一致的假设子集(即VSH,D是相对于D的变型空间)
概而言之,贝叶斯公式说明在我们的P(h)和P(D|h)的定义下,后验概率P(h|D)为:
其中|VSH,D|是H中与D一致的假设数量。
在我们选定的P(h)和P(D|h)取值下,每个一致的假设后验概率为(1/|VSH,D|),每个不一致假设后验概率为0。因此,每个一致的假设都是MAP假设。