贪心算法思想及实现
| 【算法思想】
贪心策略是指从问题的初始状态出发,通过若干次的贪心选择而得出最优值(或较优解)的一种解题方法。
其实,从"贪心策略"一词我们便可以看出,贪心策略总是做出在当前看来是最优的选择,也就是说贪心策略并不是从整体上加以考虑,
它所做出的选择只是在某种意义上的局部最优解,而许多问题自身的特性决定了该题运用贪心策略可以得到最优解或较优解。
【
贪心策略的理论基础--矩阵胚】
"矩阵胚"理论是一种能够确定贪心策略何时能够产生最优解的理论,虽然这套理论还很不完善,但在求解最优化问题时发挥着越来越重要的作用。
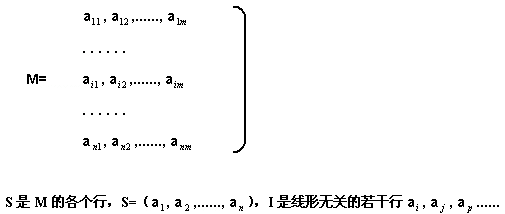
【定义[B]3】 矩阵胚是一个序对M=[S,I] ,其中S是一个有序非空集合,I是S的一个非空子集,成为S的一个独立子集。[/B]
如果M是一个N×M的矩阵的话,即:
若M是无向图G的矩阵胚的话,则S为图的边集,I是所有构成森林的一组边的子集。
如果对S的每一个元素X(X∈S)赋予一个正的权值W(X),则称矩阵胚M=(S,I)为一个加权矩阵胚。
适宜于用贪心策略来求解的许多问题都可以归结为在加权矩阵胚中找一个具有最大权值的独立子集的问题,即给定一个加权矩阵胚,M=(S,I),若能找出一个独立且具有最大可能权值的子集A,且A不被M中比它更大的独立子集所包含,那么A为最优子集,也是一个最大的独立子集。
(1)库鲁斯卡尔(Kruskal)算法矩阵胚理论对于我们判断贪心策略是否适用于某一复杂问题是十分有效的。 【 几种典型的贪心算法】 设图G=(V,E)是一简单连通图,|V| =n,|E|=m,每条边ei都给以权W , W 假定是边e 的长度(其他的也可以),i=1,2,3,...,m。求图G的总长度最短的树,这就是最短树问题。
kruskal算法的基本思想是:首先将赋权图G的边按权的升序排列,不失一般性为:e ,e ,......,e 。其中W ≤W ,然后在不构成回路的条件下择优取进权最小的边。
其流程如下:
(1) 对属于E的边进行排序得e ≤e ≤...... ≤e 。
(2) 初始化操作 w←0,T←ф ,k←0,t←0;
(3) 若t=n-1,则转(6),否则转(4)
(4) 若T∪{e }构成一回路,则作
【k←k+1,转(4)】
(5) T←T∪{ e },w←w+ w ,t←t+1,k←k+1,转(3)
(6) 输出T,w,停止。
下面我们对这个算法的合理性进行证明。
设在最短树中,有边〈v ,v 〉,连接两顶点v ,v ,边〈v ,v 〉的权为wp,若〈v ,v 〉加入到树中不能保证树的总长度最短,
那么一定有另一条边〈v ,v 〉或另两条边〈v ,v 〉、〈v ,v 〉,且w<vi,vj><wp或w<vi,vk>+w〈vk,vj〉<wp,
因为〈v ,v 〉、〈v ,v 〉不在最短树中,可知当〈v ,v 〉、〈v ,v 〉加入到树中时已构成回路,此时程序终止。
因为〈v ,v 〉∈ T,〈v ,v 〉∈T且w〈vI,vk〉+w〈vk,vj〉<w p,与程序流程矛盾。
【算法实现】
#define MAXE <最多的边数>
typedef struct {
int u;// 边的起始顶点
int v;// 边的终止顶点
int w;// 边的权值
} Edge;
void kruskal(Edge E[],int n,int e)//边的权值从小到大排列
{
int i,j,m1,m2,sn1,sn2,k;
int vset[MAXV];
for(i=0;i<n;i++)
vset[i]=i;
k=1;j=0;
while(k<n)
{
m1=E[j].u;
m2=E[j].v;
sn1=vset[m1];
sn2=vset[m2];、
if(sn1!=sn2)//两顶点属于不同的集合,是最小生成树的一条边
{
//输出这条边;
k++;
for(i=0;i<n;i++)
if(vset[i]==sn2)
vset[i]=sn1;
}
j++;
}
}
kruskal算法对边的稀疏图比较合适,时间复杂度为o(elog2e),e是边数,与顶点无关.
(2) 普林(Prim)算法
Kruskal算法采取在不构成回路的条件下,优先选择长度最短的边作为最短树的边,而Prim则是采取了另一种贪心策略。
已知图G=(V,E),V={v ,v ,v ,..., v },D=(d ) 是图G的矩阵,若〈v ,v 〉∈E,则令dij=∞,并假定dij=∞
Prim算法的基本思想是:从某一顶点(设为v )开始,令S←{v },求V\S中点与S中点v 距离最短的点,即从矩阵D的
第一行元素中找到最小的元素,设为d ,则令S←S∪ { v },继续求V\S中点与S的距离最短的点,设为v ,则令S←S∪{ v },
继续以上的步骤,直到n个顶点用n-1条边连接起来为止。
流程如下:
(1) 初始化操作:T←ф,q(1)←-1,i从2到n作
【p(i)←1,q(i)←di1】,k←1
(2) 若k≥n,则作【输出T,结束】
否则作【min←∞,j从2到n作
【若0<q(i)<min则作
【min←q(i) h←j】
】
】
(3) T←T∪{h,p(h)},q(h)←-1
(4) j从2到n作
【若d <q(j)则作【q(j)←d ,p(j)←h】】
(5) k←k+1,转(2)
算法中数组p(i)是用以记录和v 点最接近的属于S的点,q(i)则是记录了v 点和S中点的最短距离,q(i)=-1用以表示v 点已进入
集合S。算法中第四步:v 点进入S后,对不属于S中的点vj的p(j)和q(j)进行适当调整,使之分别记录了所有属于S且和S距离最短的
点和最短的距离,点v , v ,…,v 分别用1,2,…,n表示。
【算法实现】
void prim(int cost[][MAXV],int n,int v)//v是起始顶点
{
int lowcost[MAXV],min;
int closest[MAXV],i,j,k;
/*closest[i]表示U中的一个顶点,该顶点和V-U中的一个顶点构成的边(i,closese[i])具有最小的权 */
//lowcost[i]表示边(i,closet[i])的权值
for(i=0;i<n;i++)
{
lowcost[i]=cost[v][i];
closest[i]=v;
}
for(i=1;i<n;i++)
{
min=INF;
for(j=0;j<n;j++)//在(V-U)中找出离U最近的顶点K.
if(lowcost[j]!=0&&lowcost[j]<min)
{
min=lowcost[j];
k=j;
}
//输出边: closet[k]-->k;
lowcost[k]=0;//标记k已经加入U;
for(j=0;j<n;j++)//修改数组lowcost和closest
if(cost[k][j]!=0&&cost[k][j]<lowcost[j])
{
lowcost[j]=cost[k][j];
closest[j]=k;
}
}
}
|