Trie树是一棵度 m ≥ 2 的树,它的每一层分支不是靠整个关键码的值来确定,而是由关键码的一个分量来确定。
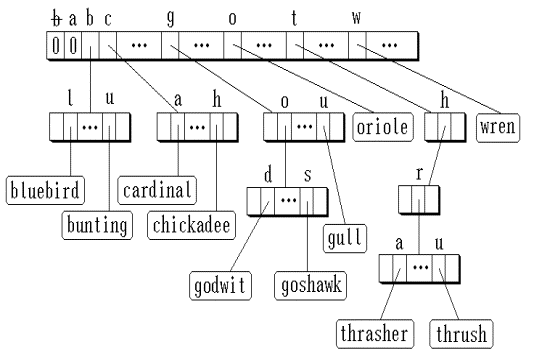
如下图所示Trie树,关键码由英文字母组成。它包括两类结点:元素结点和分支结点。元素结点包含整个key数据;分支结点有27个指针,其中有一个空白字符‘b’,用来终结关键码;其它用来标识‘a’, ‘b’,..., ‘z’等26个英文字母。
在第0层,所有的关键码根据它们第0位字符, 被划分到互不相交的27个类中。
因此,root→brch.link[i] 指向一棵子Trie树,该子Trie树上所包含的所有关键码都是以第 i 个英文字母开头。
若某一关键码第 j 位字母在英文字母表中顺序为 i ( i = 0, 1, ?, 26 ), 则它在Trie树的第 j 层分支结点中从第 i 个指针向下找第 j+1 位字母所在结点。当一棵子Trie树上只有一个关键码时,就由一个元素结点来代替。在这个结点中包含有关键码,以及其它相关的信息,如对应数据对象的存放 地址等。
Trie树的类定义:
const int MaxKeySize = 25; //关键码最大位数
typedef struct { //关键码类型
char ch[MaxKeySize]; //关键码存放数组
int currentSize; //关键码当前位数
} KeyType;
class TrieNode { //Trie树结点类定义
friend class Trie;
protected:
enum { branch, element } NodeType; //结点类型
union NodeType { //根据结点类型的两种结构
struct { //分支结点
int num; //本结点关键码个数
TrieNode *link[27]; //指针数组
} brch;
struct { //元素结点
KeyType key; //关键码
recordNode *recptr; //指向数据对象指针
} elem;
}
}
class Trie { //Trie树的类定义
private:
TrieNode *root, *current;
public:
RecordNode* Search ( const keyType & );
int Insert ( const KeyType & );
int Delete ( const KeyType & );
}
10.3.2 Trie树的搜索
为了在Trie树上进行搜索,要求把关键码分解成一些字符元素, 并根据这些字符向下进行分支。
函数 Search 设定 current = NULL, 表示不指示任何一个分支结点, 如果 current 指向一个元素结点 elem,则 current→elem.key 是 current 所指结点中的关键码。
Trie树的搜索算法:
RecordNode* Trie::Search ( const KeyType & x ) {
k = x.key;
concatenate ( k, ‘b’ );
current = root;
int i = 0; //扫描初始化
while ( current != NULL && current→NodeType != element && i <= x.ch[i] ) {
current = current→brch.link[ord (x.ch[i])];
i = i++;
};
if ( current != NULL && current→NodeType == element && current→elem.key == x )
return current→recptr;
else
return NULL;
}
经验证,Trie树的搜索算法在最坏情况下搜索的时间代价是 O(l)。其中, l 是Trie树的层数(包括分支结点和元素结点在内)。
在用作索引时,Trie树的所有结点都驻留在磁盘上。搜索时最多做 l 次磁盘存取。
当结点驻留在磁盘上时,不能使用C++的指针 (pointer) 类型, 因为C++不允许指针的输入 / 输出。在结点中的 link 指针可改用整型(integer) 实现。
10.3.3 在Trie树上的插入和删除
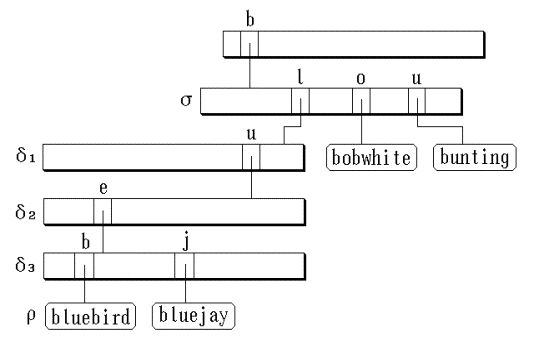
示例:插入关键码bobwhite和bluejay。
a. 插入 x = bobwhite 时,首先搜索Trie树寻找 bobwhite 所在的结点。
b. 如果找到结点, 并发现该结点的 link[‘o’] = NULL。x不在Trie树中, 可以在该处插入。插入结果参看图。
c. 插入 x = bluejay时,用Trie树搜索算法可找到包含有 bluebird 的元素结点,关键码bluebird 和 bluejay 是两个不同的值,它们在第5个字母处不匹配。从 Trie树沿搜索路径,在第4层分支。插入结果参看图。
在Trie树上插入bobwhite和bluejay后的结果 :
示例:考虑在上图所示Trie树中删除bobwhite。此时,只要将该结点link[‘o’]置为0 (NULL)即可,Trie树的其它部分不需要改变。
考虑删除 bluejay。删除之后在标记为δ3 的子Trie树中只剩下一个关键码,这表明可以删去结点δ3 ,同时结点 ρ 向上移动一层。对结点δ2 和δ1 可以做同样的工作,最后到达结点б。因为以б 为根的子Trie树中有多个关键码,所以它不能删去,令该结点link[‘l’] = ρ即可。
为便于Trie树的删除, 在每个分支结点中设置了一个 num 数据成员,它记载了结点中子女的数目。
Trie,又称单词查找树,是一种树形结构,用于保存大量的字符串。它的优点是:利用字符串的公共前缀来节约存储空间。
性质
它有3个基本性质:
- 根节点不包含字符,除根节点外每一个节点都只包含一个字符。
- 从根节点到某一节点,路径上经过的字符连接起来,为该节点对应的字符串。
- 每个节点的所有子节点包含的字符都不相同。
例子
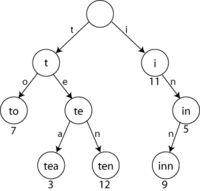
这是一个Trie结构的例子:
在这个Trie结构中,保存了t、to、te、tea、ten、i、in、inn这8个字符串,仅占用8个字节(不包括指针占用的空间)
问题:
一、 一个文本文件有多行,每行为一个URL。请编写代码,统计出URL中的文件名及出现次数。
a) 文件名不包括域名、路径和URL参数,例如http://www.rs.com/n.op/q/rs?id=1中的文件名是rs。
b) 部分URL可能没有文件名,例如http://www.abc.com/,这类统计为“空文件名”。
c) 出现在不同URL中的相同文件名视为同一文件名,例如http://www.ceshi.com/hi.php和ftp://ftp.cdef.com/hi.php为同一文件名
文件内容示例如下:
http://www.test.com/abc/de/fg.php?id=1&url=http://www.test.com/index.html
http://www.ceshi.com/hi.jsp
ftp://ftp.ceshi.com/hi.jsp
http://www.hello.com/cw/hi.jsp?k=8
http://www.hi.com/jk/l.html?id=1&s=a.html
http://www.rs.com/n.op/q/rs?id=1
http://www.abc.com/
二、 一个简单的论坛系统,以数据库储存如下数据:
用户名,email,主页,电话,联系地址,发帖标题,发帖内容,回复标题,回复内容。
每天论坛访问量300万左右,更新帖子10万左右。
请给出数据库表结构设计,并结合范式简要说明设计思路。
三、 现有两个文件,
a)数据文件A,格式为:关键词、IP地址、时间,记录条数为1000万左右,该文件是无序排列的。
b)数据文件B是关键词ID到关键词的对应表文件,格式为:ID、关键词,记录条数在100万左右,也是无序排列的。该对应表中的记录是一一对应的,不存在ID或者关键词重复的情况。
要求将数据文件A对应的关键词替换为B中的ID,生成新的数据文件C,数据文件C的格式为:关键词ID、IP地址、时间。
请设计一个程序,实现上述功能,并分析时间复杂度和空间复杂度。运行程序所使用的服务器的内存为1G,硬盘足够大。(至少要给出关键算法和设计思路)
第一题
简评
百度的主要业务是搜索,搜索的基本原理如下
1.编写爬虫程序到互联网上抓取网页海量的网页。
2.将抓取来的网页通过抽取,以一定的格式保存在能快速检索的文件系统中。
3.把用户输入的字符串进行拆分成关键字去文件系统中查询并返回结果。
由以上3点可见,字符串的分析,抽取在搜索引擎中的地位是何等重要。
因此,百度的笔试面试题中,出现这样的题就变得理所当然了。
以下是该题的java实现,代码如下:
import java.net.*; import java.io.*; import java.util.*;
/** * @author tzy * 在j2sdk 1.4.2 下测试通过 */ public class FileNameStat { private String srcPath;//要统计的文件路径 private Map statMap;//用于统计的map public FileNameStat(String srcPath) { this.srcPath=srcPath; statMap=new TreeMap(); } /*获得要统计的URL的文件名*/ public String getFileName(String urlString) { URL url=null; String filePath=null; String fileName=null; try { url=new URL(urlString); filePath=url.getPath(); int index=0; if ((index=filePath.lastIndexOf("/"))!=-1) { fileName=filePath.substring(index+1); } else { fileName=""; } } catch(MalformedURLException e) { } return fileName; } /*统计指定文件名的个数*/ public void stat(String filename) { Integer count=null; if(statMap.get(filename)!=null) { count=(Integer)statMap.get(filename); count=new Integer(count.intValue()+1); } else { count=new Integer(1); } statMap.put(filename,count); } /*统计的主方法*/ public void start() throws FileNotFoundException,IOException { BufferedReader bfin=new BufferedReader(new FileReader(this.srcPath)); String temp=null; while((temp=bfin.readLine())!=null) { stat(getFileName(temp)); } } /*输出统计结果*/ public void result() { Iterator it=statMap.entrySet().iterator(); while(it.hasNext()) { Map.Entry entry=(Map.Entry)(it.next()); System.out.println((entry.getKey().equals("")?"空文件名":entry.getKey()) + "的个数是" + entry.getValue()); } } public static void main(String[] args) throws Exception { FileNameStat fns=new FileNameStat("src.txt");//指定成待统计文件 fns.start(); fns.result(); } } |
第二题