计科1111-1114班第五周讲义、课外作业（强连通分量、BFS，截止日期：2014年4月11日23点-周五晚，学委飞信通知同学）

    第五周主要讲授了 "第3章：图的分解"的有向图强连通分量，以及“第4章：图的路径”中BFS算法。

讲授内容

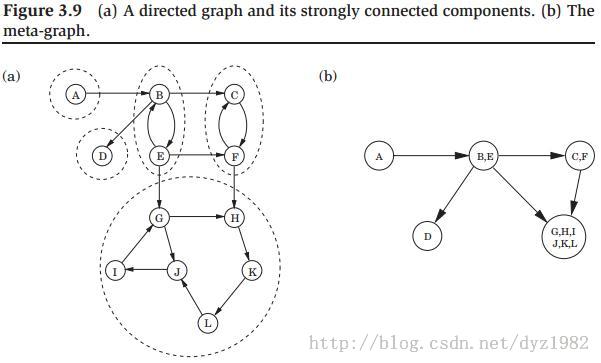
1.  强连通分量（SSC-Strong Connectivity Component）：SSC的主要算法，是建立在深度优先搜索（DFS）和 有向无环图（DAG）的概念之上。教材P105的两个性质，其中“性质：在有向无环图中，每条边都指向一个post值更小的顶点”，换句话就是，“源点的post值最大”，因为源点指向其他顶点；“性质：每个有向无环图至少含有一个源点和一个汇点”，那么就很自然的引申出了 强连通分量 的发现算法。

    有向图G的超图是一个有向无环图，其反向图Gr也是一个有向无环图，其中G的源点成了Gr的汇点，G的汇点成了Gr的源点。所以，我们可以利用Gr，在深度优先搜索过程中，找到post最大的顶点，并且对顶点按照post值进行逆序（假设其顶点逆序为：GIJLKH  D  CF  BE  A，其中共有5个强连通分量）。则在原图G中，就是依次在汇点强连通分量中的顶点（顶点G）出发，进行深度优先遍历，从而不断的找到第一个汇点强连通分量（GHKLJI），标记好已经搜索的顶点；然后继续从顶点D开始搜索，得到第二个强连通分量D；……核心：深度优先搜索中顶点的搜索顺序至关重要。

2. （重点）有向图G（V，E）的强连通分量发现算法：（a）生成G的反向图Gr；（b）对反向图Gr进行DFS搜索，得到顶点post的逆序数组；（c）按照顶点post的逆序，在原图中进行深度优先遍历。

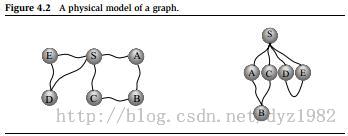
3.  广度优先搜索（BFS-Breadth First Search）：特别适合用邻接表来表示图，与BFS搜索的顺序配合完美。算法中最核心的部分就是使用队列（Queue），利用其先进先出（FIFO）的性质，算法伪代码在教材P121.

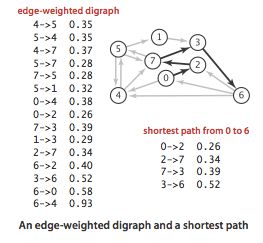
4. （重点）加权图单源最短路径算法-Dijkstra算法：其核心就是怎样把BFS算法改造一下，适合加权图，其中最大的改进就是对顶点的搜索顺序（？？强连通分量中也是这样），通过使用优先队列（Priority Queue）一下子就解决问题了。具体算法及示意图，请查阅教材P126-127。优先队列（最小堆）有三个关键操作：插入新节点（即构造过程，自下而上的冒泡P132）、删除最小值节点（会带来自上而下过滤过程，P132）、节点键值的更新（向上冒泡）。

下载与链接

1. Java队列的使用（http://blog.csdn.net/guijava/article/details/3784658）

2. 优先队列的实现（http://blog.csdn.net/changyuanchn/article/details/14564403）

3. Waze地图（大数据处理，被Google公司收购）http://www.huxiu.com/article/15893/1.html，又一笔10亿美金收购诞生！谷歌成功收购社交地图应用Waze，狙击Facebook

4. 强连通分量的实现（http://algs4.cs.princeton.edu/42directed/）

5. BFS介绍与实现（http://algs4.cs.princeton.edu/44sp/）

作业要求

1. 请各班学委飞信通知同学完成作业。 
2. 作业计入平时成绩，计分依据为大家的完成程度——态度（做 / 未做）。老师会根据大家作业的质量选择若干学生进行评论，以及提供个性化教学的依据。请大家依据自身能力，尽可能提供高水平的作业，为提高自身能力全力以赴。
3. 本次作业，老师主要检查本班学号位于11-20号的同学 和 申请免签到的同学，以及抽查部分其他同学，请大家相互转告。

作业内容

    大家至少完成作业1，以后从事IT行业的严格要求自己，尽可能完成1，2，3。

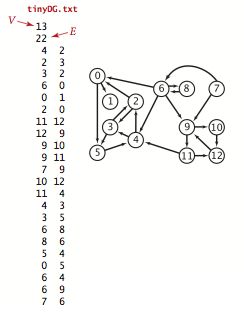
1. 有向图中反向图构造。对tinyDG.txt（http://pan.baidu.com/s/1o6jWtcA）文件所表示的图，输出其邻接表表示 与 反向图的邻接表表示。类名：GraphReverse。博文标题：第五周作业——有向图邻接表表示及反向图构造

邻接表表示示例如下：

0:1 5

1:

2:0 3

……

2. 有向图强连通分量的编程实现。对tinyDG.txt（http://pan.baidu.com/s/1o6jWtcA）文件所表示的图，输出其反向图中顶点post的逆序表示，并输出每一个强连通分量，输出图的超图（思考，or实现），类名：GraphSSC。博文标题：第五周作业——有向图强连通分量的编程实现

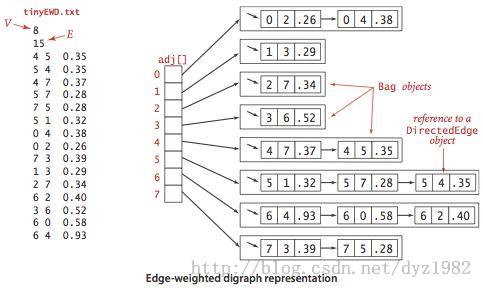
3. Dijkstra算法的实现。对加权图（tinyEWD.txt，mediumEWD.txt），计算从顶点0出发到其他顶点的最短路径，要求输出其从顶点0到每个顶点的路径，以及相应的路径距离。类名：GraphDijkstra。博文标题：第五周作业——Dijkstra算法的实现

 

提前预习

4.5 优先队列的实现

4.6 含有负边的图的最短路径（Bellman-Ford算法）

4.7 有向无环图的最短路径

5.1贪心算法-最小生成树

推荐阅读

    无意中搜索到一篇网易丁磊的演讲（丁磊浙大演讲实录:一定要做你喜欢做的事情），因为只有自己感兴趣，才会全身心的投入进去，即使当时看起来投入没有收获，但世界是公平的，长时间来看，收获与付出一定是成正比，即使对于个人的幸福满意度来说也是如此。老师和大家一样，在大学、研究生、工作的时候，也都迷茫过，走过很多弯路。现在对于大学，最后悔的事情就是没有发现自己的兴趣所在，没有能够尽情的投入去做一件事情；而研究生阶段（博士）的第3年，我很想退学，因为看不到前途，后来在朋友、导师的劝说下坚持了下来，从本科到博士，一共读了9.5年。毕业后去南京工作，然后离职去开办农场，失败后来海大，误入传销，再逐步找到自身的兴趣——教育、尽可能和学生做朋友。

    即使是目前在做自己喜欢的事情，也遇到了各种各样的挫折与困难，也不是会一帆风顺。如现在对于《算法》课的学习方式，还是有很多不满意的地方，因为看到大家收获不多，所以一直在调整（因为有兴趣，目标明确，所以即使是一条曲折的道路，也是逐渐接近目标）。短期来看，我们使用CSDN博客交作业，也看不出成效；而有部分同学会逐渐发现——写博文、总结，能够更有效的进行思考，达到输入理解。就像我现在布置作业，也是一个再思考的过程，对有些概念理解得更加深入。

    学习，一定要有主动性，对自己负责。没人可以强迫大家做好一件事情，只有自己可以。所以，老师希望大家有明确目标的时候，能够勇敢的往前走。然后，很多同学和老师当年一样，没有明确的兴趣志向，迷茫中求学，这时候应该怎么办呢？

    迷茫中，我们做好当下的事情。这就是老师的建议，时间是最公平的财富，可以用来看电影，打游戏，也可以用来提高自己、阅读等。当我们毕业去找工作的时候，场景1：求职时，如果你是老板，在面试一个同学时，同学的成绩很一般（挂科2-3门，大部分60-70分），值得分享的经历很少，失败的事情很少，表达一般，作为老板，你会招聘这样的员工吗？场景2：求职同学学习成绩都不错，谈兴趣，答道对IT兴趣不大，但目前对其他方面也比较迷茫，所以在大学里就把该学好的功课做好，希望在工作中，能够在压力环境中找到自己的兴趣；谈到优点，有主动负责的精神，做好小事，乐意为他人服务（如大学时，俞敏洪为室友打过4年开水，真的不是白打，因为这其中有一种坚持的力量），班级有一位同学，每次上课前都默默的擦黑板，一次不奇怪，但一直在做，这就是品格的力量，如果我公司招聘，我一定会招聘他。场景3：该同学成绩差异很大，专业课分数很高，英语、马邓等60来分，参加过2-3个比赛，获过一次省级以上的比赛奖励，做过的产品发布到网络后，还有100个以上的下载量；在自身的博客中，发表了超过100篇以上的原创文章，而且有一定的系统性与深度。如果我是公司老板，首先问的问题是，你对公司有什么要求与希望？    在大学，100个同学中，场景3中同学在10个以内，场景2中的同学在20-30个，场景1的同学在20-30个左右，还有一些其他发现自身对其他方面的兴趣，非常投入的去做了很多其他的事情。

    因为对于公司，华南理工大学陈春花教授的公开课中讲到，公司是绩效第一，任何员工对组织的作用，就是看是否能够为组织创造价值，先讲贡献，再谈回报，你们工作以后会理解得更深，在平时的兼职中也可以体会到。

    我，目前肯定不是一个优秀的教师，但我一直在努力朝着这个目标前进。也许当同学们5年之后回母校参观时，那时的学生会更有收获。让我们一起努力！没有尝试，就没有失败；没有坚持，就没有成功，也永远不会体会到失败的辛酸与成功的泪水。唯有行动，是我们现在应该做到的事情。

    在我们的 总成绩=平时成绩+期末成绩+加分 中，加分题是一些编程题，如果大家对编程以外的领域非常想尝试，也可以分享给老师，老师可以把同学的想法增加到“加分”部分。因为，任何外在的激励，都只是一个诱因，唯有内心的主动性，我们才会做得更好。加分题，今天会发布出来，希望有更多的同学，愿意主动去尝试，去实践，去体验其中的坚持与梦想。