与Scheme共舞
发表在《程序员》2007年7月刊上。不log上写帖子不用考虑版面限制,所以这里的帖子比发表的啰嗦点。赵健平编辑,Jacky,和刘未鹏都给了我很多帮助,在这里一并谢了。免费的Scheme实现很多。我用的是PLT Scheme,可以到这里下载。PLT Scheme的IDE(Dr. Scheme)支持Emacs的键盘绑定,用emacs的老大们应该喜欢。Dr.Scheme内置中文支持:
下面是正文:
不能影响你思考方式的编程语言不值得学习 – Alan Perlis [1]
不少朋友问,为什么要学Scheme这样无数括号包裹的语言。答案很简单:帮你理解计算的本质,成为更优秀的程序员。Scheme好比大还丹。没人拿药丸儿当板砖拍人,但服了它却能指望十步杀一人,千里不留行。
1975年问世的Scheme是Lisp方言。所以不妨从Lisp谈起。Lisp是一门传奇语言,诞生50年,仍然影响深远。程序员们似乎不断“发现”Lisp里简单却深刻,浅显但强大的特性,并应用到不同地方,取得非凡成就。比如最近热火的Ruby、Python、以及JavaScript中许多为人称道的功能源于Lisp。也许John K. Foderaro的比喻和总结最能说明Lisp的价值:Lisp好比变色龙,高度适应环境的改变,因为
它是一门可以编程的编程语言。我们不仅可以用Lisp编程,还可以对Lisp编程
[2]。Lisp内置的抽象方法让Lisp程序员们身段灵活,长袖善舞。每当新的编程范式出现,Lisp程序员们总能快速实现相关功能,甚至做出进一步改进。比如Smalltalk展示面向对象编程的潜力后,MIT媒体实验室的Cannon Howard便在1982年推出Flavors,一个功能丰富的面向对象扩展。Cannon的扩展不仅实现了 当时流行的面向对象功能,还首创了多继承,多重分派,以及被Ruby程序员狂赞的mixin
[3]。尔后在Xerox PARC的 Gregor Kiczales又在集大成的Common Lisp面向对象扩展 — CLOS — 里加入面向方面(AOP)的编程方法
[4]。Gregor也是面向方面编程的发起人和AspectJ的作者。熟悉Java的老大应该对他不陌生。其实CLOS支持的method combination已经支持AOP里的before/after/around处理。AOP和CLOS出于同一人之手,应该不是巧合。顺便说一句,Gregor1993年的名作 The Art of Meta Object Protocol也值得细读。
传奇语言自有传奇历史。1958年,John McCarthy从达特茅斯搬到MIT。当时人工智能的另一奠基人Marvin Minsky也在那里。牛人相见,好比利刃相击,火花耀眼。著名的MIT人工智能计划上马
[5]。研究AI的过程中,McCarthy需要一门编程语言描述他的理论模型。当时人见人爱的图灵机只有一套笨拙的语言,不适合干净利落地表达复杂的递归函数,所以McCarthy在丘齐的lambda算子基础上设计了Lisp。早期的Lisp是纯理论工具,用来帮助项目组进行程序的推导和证明。实在需要用机器验证理论了,研究组的老大们就手工把Lisp程序翻译成IBM 740的汇编代码,再上载到IBM 740上运行。人肉编译器们甚至热衷于编译各式Lisp程序,觉得跟解智力题一样好玩儿。他们还证明了可以用Lisp写出一个通用函数eval(), 用来解释执行Lisp的表达式
[6]。但他们光顾赞叹eval()和元图灵机一样彪悍,且比图灵机构造出元图灵机的代码美妙,并没想到eval就是一个通用的Lisp解释器。幸好有天McCarthy的学生S.R. Russell灵机闪现,连夜用IBM704的机器语言实现eval()。于是世界上第一个Lisp解释器横空出世,绿色低功耗无污染的人肉编译才渐渐失传。那时真是计算机科学研究的黄金时代啊,人们可以一夜之间改变世界,比居委会大妈在股市一夜暴富还来得轻快。顺便提一下,我们习以为常的条件判断语句,也是McCarthy在Lisp里发明的。而为了让函数应用没有副作用和实现函数闭包,McCarthy的研究小组又顺便发明了垃圾收集。1975年,同是MIT的Gerald Jay Sussman和Guy Steele为了研究Carl Hewitt的面向对象模型,用Lisp编写了一个玩具语言。这个玩具语言简化了当时流行的Lisp语法,引入了词法定界(又叫静态范围)和Continuation两大革新。Sussman和Steele给这门语言取名Schemer,希望它发展成像AI里著名系统Planner一样的有力工具。可惜当时MIT用的操作系统ITS只允许最长6个字节的文件名。Sussman和Steele不得不把Schemer的最后一个字幕’r’去掉。Scheme问世便显露峥嵘:Sussman和Steele很快发现Scheme的函数和Hewitt模型里的演员(也就是我们现在所谓的对象)没有本质区别,连句法都基本一致
[7]。事实上,Sussman在教材《计算机程序设计与解释》的第二章用短短几十行代码展示了一套面向对象系统。
Scheme是极度简化的语言。他的规范文档不过47页
[8]。相比Lisp另一大分支Common Lisp规范的上千页文档或者Java规范的500来页文档,可见Scheme的短小精悍。不过,我们仍然可用Scheme写出优雅犀利的程序。Scheme规范R
5RS开篇道出了Scheme的设计宗旨:设计编程语言时不应堆砌功能,而应去掉让多余功能显得必要的弱点和限制。Smalltalk的发明人Alan Kay在一次访谈录中提到,Lisp是编程语言中的麦克斯韦方程组
[9]。这句评价用到Scheme上更为合适。Scheme甚至让我们写出用其他语言无法轻易写出的程序。Sussman和Steele用Scheme探索不同的编程模型时时,往往一周做出十来种不同的解释器,可以旁证Scheme的简洁和灵活。在解释是什么造就了Scheme的精练与生猛之前,我们先介绍一下Scheme的基本元素:
- Scheme的语法结构 大道至简。Scheme的结构就两种:原子和表达式。原子是诸如数,字符串,布尔值,变量,空表这类简单数据。对非变量的原子求值,得到原子自身。对变量求值,得到变量绑定的值。比如说,对1求值得到1,但如果对变量A求值,而A和字符串”A”绑定,则得到字符串“A”。表达式的形式也只有一种:列表。一对括号包含起来的就是列表。表里的元素用空格分开。列表可以嵌套。这样的表达式在Lisp里叫做S-表达式,意思是符号表达式。下面是一些例子:
- ( ): 一个空表
- (1 2 3 4 5):一个包含五个整数的表
- (1 “a” 1.5 #t #f):一个列表,依次包含整数、字符串、浮点数、为真的布尔值、和为假的布尔值
- (1 (2 3) ):一个嵌套列表,第二个元素(2 3)也是一个表
- (+ 2 3):一个表达式,表示把2和3相加。Scheme里所有的操作符都是前缀操作符,即操作符在前,操作数据在后。比如说4 * (2 + 3)在Scheme里表达为(* 4 (+ 2 3))。很多人看不管这种方式。不过仔细思考一下,可以看出前置操作符让任何操作符都是多维的。比如说。如果我们要把1到5的整数相加,用中缀操作符,就得写成 1 + 2 + 3 + 4 + 5。同一个加好重复了4次。而用前缀操作符,只需要写一次:(+ 1 2 3 4 5)。推而广之,如果我们要把一列数加起来,就得用到循环。而在Scheme里则不需要。而且前缀操作符去掉了优先级问题:我们可以通过括号来判断每个表达式的优先级。
- (lambda (x y) (sqrt (* x y))。这个表达式定义了一个匿名函数,计算并返回参数x和y的几何平均值。当一个表达式以lambda开头的时后,我们就知道要定义一个函数了。
- (define zero 0):这个表达式把一个变量zero绑定到一个整数0。在Scheme里,所有变量本质上都是指针。指针本身没有类型,他们指向的值才有类型。换句话说,Scheme是动态类型语言。
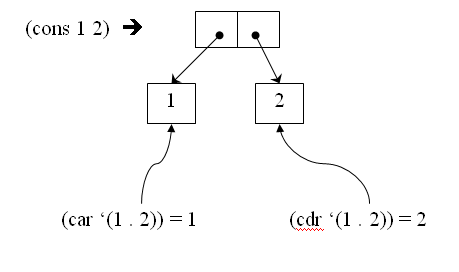
- (car ‘(1 2 3 4)):这个表达式调用函数car。函数car接收一个列表参数,并返回这个参数的第一个值,也就是1。注意例子里的参数(1 2 3 4)前有一单引号。这是因为Scheme总是把一个普通列表当作表达式计算。加上单引号相当于告诉Scheme,不要对(1 2 3 4)估值,把它当成数据对待。如果不加这个单引号,Scheme会执行(1 2 3 4)。执行的规则是把该列表的第一个元素当成函数来调用。而第一个元素是1,不是函数,Scheme会抛出错误。
- (cdr ‘(1 2 3 4)): 这个表达式调用函数cdr(读作kuder)。函数cdr也是把一个列表作为参数,并返回这个列表除去第一个元素后的子表。所以对(cdr ‘(1 2 3 4))求值,就得到(2 3 4)。
- Scheme的数据类型 Scheme提供了各种通用的数据类型:整数,浮点数,复数,有理数,字符串,布尔变量,散列,数组,矢量,点对,和列表。值得一提的是点对(pair)和列表。这俩哥们儿是Scheme编程的基石。还是用例子说明比较好:
- 不要小看了列表。这个看似简单的数据类型的具有丰富的表达能力。比如我们可以把下面2x3的矩阵表达为((1 2 3) (4 5 6) (7 8 9)):
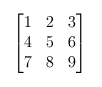 而下面的树也可以用列表直观表达:(A B C (D (F H) G) E)。也就是说,每个列表表示一个树或子树。列表的第一个元素是根。
而下面的树也可以用列表直观表达:(A B C (D (F H) G) E)。也就是说,每个列表表示一个树或子树。列表的第一个元素是根。 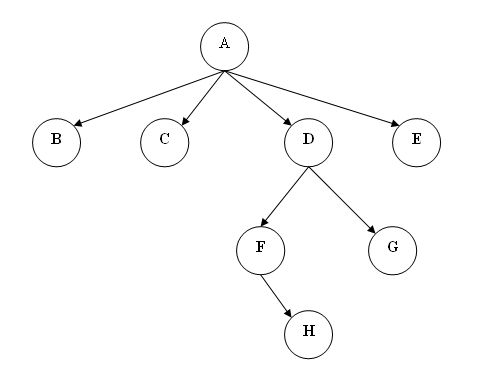
- 函数 函数在Scheme里是一等公民。定义的函数可以被当成数据传递或返回。有三种定义函数的方法:
- 用lambda操作符定义一个匿名函数。比如(lambda (x) (* 2 x))定义了一个函数,返回参数x的倍数。操作符lambda后第一个子列表是参数列表,而第二个子列表是函数定义。这和JavaScript里的匿名函数没有本质区别: function(x){return 2 * x;}
- 用define绑定函数名:(define 1+ (lambda (x) (+ 1 x)))。这个例子定义了递加函数,并把它绑定到函数名1+上。。Scheme对函数名没有限制。事实上,Scheme对所有函数名一视同仁。规范里定义的函数没有特殊地位,我们完全可以用自己的函数定义取代。这相当于下面的JavaScript语法: var increment = function(x){return x + 1;}。
- Scheme还提供了一条捷径,省去lambda。下面的例子用大小比较定义相等函数。函数名是same? 而参数就是后面的x和y。 (define (same? x y) (not (or (> x y) (< x y))) 这样的定义方式和JavaScript里的常用函数定义方式一致。呵呵,可以看出JavaScript从哪里获得灵感的了吧?下面是等价的JavaScript定义: function isSame(x, y){ return !((x > y) || (x < y)); }
很多老大看不惯括号。其实Lisp刚诞生时,John McCarthy设计了叫M-表达式的语法,与C/C++的语法类似。比如S-表达式(cdr ‘(1 2 3)用M-表达式就写成cdr[1, 2, 3]。但是Lisp的程序员们纷纷放弃了M-表达式,选择直接使用S-表达式。S-表达式的实质是用抽象句法树(AST)表达程序,直接省去了解析这道工序。比如说,a+b*c解析成AST后,和下图一致。而该AST的表示不正好是(+ a (* b c))么? 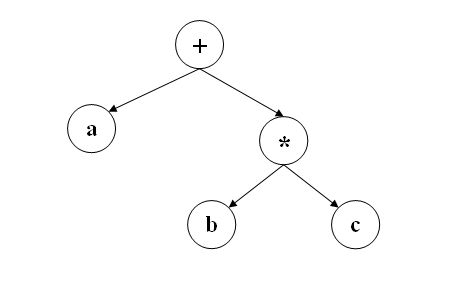 更重要的是,既然程序就是句法树,程序和数据的表示就统一了。程序即数据,数据即程序。我们遍历列表修改数据。同理,我们也可以遍列类表修改程序。正是这样的统一处理带给Scheme无与伦比的威力:无论是编译时还是运行时,我们都可以修改,注入,加载,或者生成新的程序 — 这些无非是在AST里修改或添加节点而已。我们甚至可以改动或添加新的句法。
更重要的是,既然程序就是句法树,程序和数据的表示就统一了。程序即数据,数据即程序。我们遍历列表修改数据。同理,我们也可以遍列类表修改程序。正是这样的统一处理带给Scheme无与伦比的威力:无论是编译时还是运行时,我们都可以修改,注入,加载,或者生成新的程序 — 这些无非是在AST里修改或添加节点而已。我们甚至可以改动或添加新的句法。
明了这些基本概念,就可以领略Scheme的妙处了。Scheme最为人称道的功能之一是它的函数编程能力。所谓函数编程,是指用一系列函数应用实现程序。每个函数接受参数,计算后返回结果。计算过程中没有副作用,不改变任何变量的状态。同时,函数本身是一等公民,可以作为数据传入另外的函数,也可以作为结果被其它函数返回。这样的好处是什么嗫?一言以蔽之:黏合
[10]。我们用简单的函数描述系统的不同功能。每个函数高内聚,低耦合(参数进,结果出。没有副作用。想低内聚高耦合都不容易)。Scheme提供许多方便的工具把这些函数黏合起来。这种高度支持模块化编程的能力绝对让人惊叹。多说无益。看例子。
§ 定义一个函数sum-of-squares计算一列数的平方和。比如说(sum-of-squares ‘(1 2 3 4))返回的结果是30。下面是Scheme的代码。
 测试结果:
测试结果:
 如果哪位老大不觉得这个函数定义优雅的话,不妨试试用命令编程的方式重写。比如说用C,用Java,或者用Pascal。 解剖一下上面的函数定义:
如果哪位老大不觉得这个函数定义优雅的话,不妨试试用命令编程的方式重写。比如说用C,用Java,或者用Pascal。 解剖一下上面的函数定义:
 如果哪位老大不觉得这个函数定义优雅的话,不妨试试用命令编程的方式重写。比如说用C,用Java,或者用Pascal。 解剖一下上面的函数定义:
如果哪位老大不觉得这个函数定义优雅的话,不妨试试用命令编程的方式重写。比如说用C,用Java,或者用Pascal。 解剖一下上面的函数定义:
o 第一行 (define (sum-of-squares numbers) 表示定义一个函数。函数名为sum-of-squares,而函数接受一个参数。
o 第二行是函数的定义。计算顺序是:先调用函数map,在把函数+(Scheme里一切都是函数。相加也是函数)应用到得到的结果上。
o 函数map是一个高端函数。所谓高端,是指这个函数可以接受或返回函数。函数map接受两个或多个参数。第一个参数必须是函数,而其它参数则必须是列表。函数map会同步遍历所有的列表,并把第一个参数应用到遍历时遇上的每个元素,并把结果放到一个新表里。在上面的例子里,函数map的第一个参数是个匿名函数:(lambda (x) (* x x))。这个匿名函数接受一个参数,x,并返回x的平方。我们来看看(map (lambda (x) (* x x)) ‘(1 2 3))这个例子:map从遍历列表(1 2 3)开始,一次取出1, 2, 最后3。对每个取出的元素,应用第一个参数定义的函数。比如取出2时,应用(lambda (x) (* x x))就得到(* 2 2),结果为4。所以最后的结果就是(1 4 9)。
o 顾名思义,函数apply负责应用函数。它接受两个参数。第一个参数是函数,第二个参数必须是列表。列表对应被应用函数接受的参数列表。比如说,(apply + ‘(1 2 3 4))就是把相加应用到参数(1 2 3 4)上,和(+ 1 2 3 4)等价。这里也显出了用前缀操作符的好处:每个函数都可以接受任意多个参数。再举个例子:(apply car ‘((a b c d)))等价与(car ‘(a b c d)),得到的结果是a。注意哈,函数apply的最后一个参数在传入第一个参数代表的函数时,最外面的一层括号被剥去。所以我们要把列表(a b c d)传给函数car,就得写成((a b c d))。
我们在编程里往往需要处理一系列数据,比如说把对一列整数求和,找出一个文件中每行里的电话号码,把一列数据转换成另外一列数据。。。如果在普通的命令式语言里,我们会用各式循环来处理。问题是,其实这些循环极其相似:遍历列表中每个数据,对每个数据做出一定的处理。遍历本身都是一样的,不同的只是处理数据的方式。而Scheme正是通过函数map抽象出了遍历的普遍形式。处理数据的具体例子被抽象成了函数。最后通过高端函数这个“黏合剂”,让我们享受到如此妖娆的代码。熟悉 Google MapReduce, Apache Hadoop,或者 Ruby Starfish的老大们又猜对了:MapReduce的灵感来自函数编程里常用的map和reduce函数。MapReduce本身是用C++写的。这多少可以说明,哪怕我们只用主流编程语言,学习其它编程范式也能增长我们的功力。
§ 再来一个例子:求出两个矢量的点乘。比如说[a, b, c, d] x [e, f, g, h]就等于a*e + b*f + c*g + d*h。如果我们定义函数dot-product, 那么(dot-product ‘(1 2 3 4) ‘(5 6 7 8))就等于1x5+2x6+3x7+4x8 = 70:
 这次函数map同步遍历两个列表,所以定义的匿名函数也接受两个参数。Scheme里的map函数可以同时遍历任意多个列表。Scheme里的函数调用都是S-表达式列表。所以遍历一个列表也好,多个列表也好,都是处理一个S-表达式的尾巴,没有本质区别。哪位老大有兴趣,不妨了解了Scheme宏的用法(后面会讨论)后,实现自己的map函数。
这次函数map同步遍历两个列表,所以定义的匿名函数也接受两个参数。Scheme里的map函数可以同时遍历任意多个列表。Scheme里的函数调用都是S-表达式列表。所以遍历一个列表也好,多个列表也好,都是处理一个S-表达式的尾巴,没有本质区别。哪位老大有兴趣,不妨了解了Scheme宏的用法(后面会讨论)后,实现自己的map函数。
 这次函数map同步遍历两个列表,所以定义的匿名函数也接受两个参数。Scheme里的map函数可以同时遍历任意多个列表。Scheme里的函数调用都是S-表达式列表。所以遍历一个列表也好,多个列表也好,都是处理一个S-表达式的尾巴,没有本质区别。哪位老大有兴趣,不妨了解了Scheme宏的用法(后面会讨论)后,实现自己的map函数。
这次函数map同步遍历两个列表,所以定义的匿名函数也接受两个参数。Scheme里的map函数可以同时遍历任意多个列表。Scheme里的函数调用都是S-表达式列表。所以遍历一个列表也好,多个列表也好,都是处理一个S-表达式的尾巴,没有本质区别。哪位老大有兴趣,不妨了解了Scheme宏的用法(后面会讨论)后,实现自己的map函数。
§ 还不够神奇?那写个矩阵转置函数怎么样? 所谓矩阵转置,是说把M x N的矩阵的行和列兑换,得到NxM的矩阵。比如下面的例子。给出矩阵A, A的转置矩阵A
T就等于矩阵B:
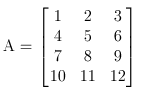
 如果我们定义了函数transpose,那么用上面的例子,调用函数(transpose ‘((1 2 3) (4 5 6) (7 8 9) (10 11 12))就应该得到((1 4 7 10) (2 5 8 11) (3 6 9 12))。实现这个函数得多少代码呢?请看—
如果我们定义了函数transpose,那么用上面的例子,调用函数(transpose ‘((1 2 3) (4 5 6) (7 8 9) (10 11 12))就应该得到((1 4 7 10) (2 5 8 11) (3 6 9 12))。实现这个函数得多少代码呢?请看—
 一行代码,四个函数。还有比这更干净利落的么?我们具体分析一下:
一行代码,四个函数。还有比这更干净利落的么?我们具体分析一下:
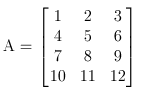
 如果我们定义了函数transpose,那么用上面的例子,调用函数(transpose ‘((1 2 3) (4 5 6) (7 8 9) (10 11 12))就应该得到((1 4 7 10) (2 5 8 11) (3 6 9 12))。实现这个函数得多少代码呢?请看—
如果我们定义了函数transpose,那么用上面的例子,调用函数(transpose ‘((1 2 3) (4 5 6) (7 8 9) (10 11 12))就应该得到((1 4 7 10) (2 5 8 11) (3 6 9 12))。实现这个函数得多少代码呢?请看—
o 和前面描述的一样,函数应用从里到外进行。所以调用(transpose matrix)时,(cons list matrix)先被执行,然后函数map被应用到执行的结果上。
o list是Scheme提供的一个函数。它接受任意参数,并把所有参数一次放到一个列表里,然后返回这个列表。比如说(list ‘a)返回(a),(list 1 2 3 4)返回(1 2 3 4)。注意这里我们不用写成(list ‘1 ‘2 ‘3 ‘4),为Scheme里,对数字计算得到数字本身。最后一个例子:(list ‘(1 2) ‘(3 4) ‘(5 6))得到((1 2) (3 4) (5 6))。
o 函数cons前面提到过。它接受两个参数,返回这两个参数合成的点对。比如说(cons ‘a ‘b)就得到(a . b),而(cons 1 ‘(2 3))就得到(1 2 3)。
o (cons list matrix)的目的是把函数list“注入”到表达式矩阵的表里。比如说,(cons list ‘((1 2 3) (4 56))就得到(list (1 2 3) (4 5 6)) 。这是什么?对了,我们轻而易举地在运行时生成了代码!
o 最后的函数应用(apply map 。。。)就清楚了。用例子最好说明:如果我们的矩阵matrix等于((1 2 3) (4 5 6)),那(cons list matrix)得到列表(list (1 2 3) (4 5 6))。自然地,(apply map (cons list matrix))等于(apply map ‘(list (1 2 3) (4 5 6)),也就等于(map list (1 2 3) (4 5 6))。计算这个表达式,当当!我们得到最后结果((1 4) (2 5) (3 6))。转置完成。
§ 在处理树状数据时,我们往往需要知道树的最大深度(最大深度也叫树的高度)。一个节点的深度等于该节点到根节点间的路径数。下图中的树最大深度为3, 路径是A->D->F->H。现在我们写一个函数来计算一棵树的深度。 
o 先得知道树的表式方式。我们就用前面提到的表示法:(A B C (D (F H) G) E)。
o 解释下出现的新函数:
o 关键字cond是条件函数,相当于C语言里的switch…case。它的语法如下: (cond ((条件1) (表达式1)) ((条件2) (表达式 2)) 。。。 ((条件 n) (表达式 n)) (else (表达式 n+1))) 也就是说,当(条件 k)的计算结果为真时,(表达式 k)会被执行。执行完后,函数cond结束。最后的符号else是特殊元素,它的计算结果总是为真,这保证了当其它条件语句不为真时,else对应的表达式肯定会被执行。
o 函数list?判断它的参数是否是列表。如果是,它返回真值,#t。不然返回假值#f。比如说,(list? ‘()) 返回 #t, (list? ‘(1 2))也返回#t,而(list? 1)返回#f。
o 这个函数怎么执行,就留给老大们当练习题吧。
如果Scheme里仅有高端函数,到现在也就不足为奇。很多语言都已支持函数编程。Python, Perl,Ruby,C#3.0都内建了各式函数编程的功能,更不必说其它的函数编程语言,比如Erlang, Haskell, OCaml等。甚至C++里都用模板搭出了一整套函数编程的类库(比如boost.lambda)。不过Scheme还有一套至今无可比拟的独门暗器:宏。说到宏,用C的老大们就笑了。用C++的老大们也笑了。好在此宏非彼宏。Scheme的宏和模板直接操作列表,根本就是Scheme语言的一部分,可以结合环境生成灵活的代码,甚至扩展Scheme故有的语法。
我们先用一个网上随处可见的例子说明C里宏的局限。假设我们需要写一个通用的求平方函数:x*x: y*y直观的写法应该是 #define SQAURE(x) x * x
如果真这样写,就错了。如果我们计算 1/SQUARE(2),宏展开为1/2*2。结果我们得到1,而不是正确的1/4。于是我们改写一下总可以了吧: #define SQUARE(x) (x*x)
还是不行!看这个例子:SQUARE(1+1),展开后变成(1+1*1+1),结果得到错误的3。于是我们把宏改写成 #define SQUARE(x) ((x)*(x))
但这样还是不行。SQUARE(x++)会被展开成((x++)*(x++)),x被错误地多递增了一次。所以我们再改: int temp; #define SQUARE(x) ({temp = x; temp * temp}) 可是这样的话这个宏只能接受整数,还引入一个全局变量,那我们还不如写成int square(x){return x * x;}。于是再改: #define SAUARE(x) /
({typedef xtype =XTYPE x; xtype temp = XTYPE x; temp*temp; }) 这下可以了,但我们以后不能直接申明int x了,得用XTYPE这个typedef定义的类型。一个如此简单的宏都要耗费这么多考量,那再复杂一点的呢?C++的模板好一些,不过看看Boost的实现,就知道C++模板最好留给类库程序员
[11]。幸好,Scheme的宏提供了完全不同的体验。它让我们把编程中重复出现的模式抽象出来。这类抽象往往和具体应用有关,不适合在短小篇幅内举例。因此,我们用模拟其它语言的功能来举例。但不要误解Scheme的宏只适合写编译器或者DSL。
先举个简单例子供老大们开牙。Perl和Ruby里有一方便的语言后置修饰,即把条件判断放到执行语句的后面。比如: print “x > y” unless y >= x
这相当于下面的语句: if(! (y >= x) ){ print “x > y” }
寥寥两三行,我们不仅有了unless这种用法,还把它做成了后置修饰。宏是这样定义的:
§ 我们用函数define-syntax定义宏,du是这个宏的名字(do-unless的缩写)。缺省情况下,宏扩展从表达式的第一个元素开始,所以我加上du作为关键字。我们可以通过修改扩展宏的函数来去掉对起首关键字的依赖,不过这无关本质。
§ 每个宏由一系列句法规则组成。这些句法规则由syntax-rules定义。函数syntax-rules规定了一到多组模式匹配的语句:(模式 模板): (syntax-rules () (模式1 模板1) (模式2 模板2) 。。。 (模式n 模板n)) Scheme会依次用列出的模板匹配定义的表达式。匹配成功的话,就扩展模板。比如说当Scheme看到(du (display “3 > 2”) unless (> 2 3))时,就开始试着用宏定义里的模式来匹配该表达式。下划线”_”是一特殊字符,指代宏的名字。匹配的结果是 _ 与”du”匹配,expression与(display “3 > 2”)匹配,而condition与(> 2 3)匹配。匹配成功,所以这个模式对应的模板被展开为(if (not (> 2 3)) (display “3 > 2”))。执行该语句,便导致“3 > 2”被打印出来。两行程序,我们便可以体验新的编程手段。还不够酷么?
我们再看一个例子。Python和Haskell支持list comprehension,用类似集合定义的语句转换已知列表。比如下面的Python程序挑出从1到10里的奇数,并把将它们乘以2。最后的结果是[2, 6, 10, 14, 18]。 [2 * x for x in range(10) if x % 2 == 1] Haskell里甚至支持对多个列表同时操作。下面的例子表示,依次取出列表[1, 3, 5]里的每个元素x,和列表[2, 4, 6]里的每个元素y, 把他们组对。得到的结果是新的列表[(1,2),(1,4),(1,6),(3,4),(3,6),(5,6)] [(x,y) | x <- [1,3,5], y <- [2,4,6]] 我们用Scheme的宏可以如魔法般实现这样雅致的功能。Scheme类库Swindle里包含了花样繁复的list comprehension功能。我们这里只实现一个阳春版的
[12],用Philip Wadler提出的转换规则
[13]:
1991年Guy Lapalme给出了Common Lisp的lisp comprehension宏定义
[14]。熟悉Lisp的老大们可以看出Lisp的句法转换明显不如Scheme的方便简洁。下面是一些测试例子:


下面的是对这个宏的解释:
- flat-map是一个简单函数。它和函数map功能类似。不过它会展平嵌套的列表。比如说(map (lambda (x) (list x)) ‘(1 2 3))的结果是((1) (2) (3)),而把map换成flat-map得到的结果是(1 2 3)。
- (define-syntax list-of。。。定义了list comprehension的句法。当系统看见list-of时,就知道要执行list comprehension了。
- (syntax-rules (<-))表示开始定义句法转换规则。关键词syntax-rules后紧跟的列表(<-)可以包含一个或多个标识符。Scheme在句法转换时会自动忽略这些标识符,不会让它们同随后的变量匹配。
- 省略号…表示匹配0个或多个标识符号。比如,模式(x …)可以同(1)匹配,也可以同(1 2)匹配,也可以同(1 a 3)匹配。
- 注意定义的句法可以递归出现,比如list-of 就出现在随后的定义里。正是递归的威力让看似复杂的list comprehension变得如此容易实现。也就是说,Scheme的宏其实是功能更为花哨的函数。
这篇帖子不能涵盖Scheme的全部功能。比如我们完全没有涉及continuation,延迟计算,或者尾递归。不过希望你领略到Scheme玲珑剔透的设计。学会它(更重要的,享受它),你会发现,一条通向计算机技术伊甸园的秘密小道出现在你脚下。
[1]
Alan Perlis, Epigrams of Programming, SIGPLAN Notices Vol. 17, No. 9(September 1982), pp7-13. Alan Perlis因为开发Algo编程语言获得1966年的图灵奖。Algo语言对命令式编程影响深远。流行多年的C,C++,和Pascal都属于Algo家族的成员。现下的热门Java和JavaScript虽然一个传承着Smalltalk的基因,一个根本就是Lisp的骨血,也要披着Algo家族句法风格的外衣。
[2] John K. Federaro, Lisp Is Chameleon,
Communications of the ACM, Volume 34, Issue 9(September 1991), pp27
,http://portal.acm.org/citation.cfm?doid=114669.114670 ACM很不厚道,看这篇文章需要ACM的帐户。
[3] 号称是这篇文章说的:Howard Cannon, Flavors -- A Non-Hierarchical Approach to Object-oriented Programming. Unpublished draft, 1979, 1992, 2003。
[4] AOP(Aspect Oriented Programming)这个名词是AspectJ小组最先提出来的,但AOP的一些基本功能,比如说before/after/around操作,早就在Gregor的CLOS里实现了。
[5] John McCarthy, History of Lisp,
History of Programming Languages, 1978, pp173-185
,http://www-formal.stanford.edu/jmc/history/lisp/lisp.html
[6] John McCarthy, Recursive Functions of Symbolic Expression and Their Computation my Machine, http://www-formal.stanford.edu/jmc/recursive/recursive.html
[7] Guy L. Steele, Richard P. Gabriel , Evolution of Lisp
, 1993.
[8] Richard Kelsey et., Revised
5 Report On the Algorithmic Language Scheme, 1998, http://www.schemers.org/Documents/Standards/R5RS/r5rs.pdf
[9] A Conversation With Alan Kay, ACM Queue, Vol 2, No. 9, Dec/Jan 2004 – 2005. http://acmqueue.com/modules.php?name=Content&pa=showpage&pid=273&page=1。Alan Kay真是人精。他的访谈向来精彩。强烈推荐。麦克斯韦方程组是詹姆斯.麦克斯韦19世纪末总结(非原创)出的一套方程组,精炼地描述了电场,磁场,电压,和电流间的关系。虽然方程组不过4个方程,却是经典电磁学的根基。
[10] John Hughs,
Why Functional Programming Matters, http://www.math.chalmers.se/~rjmh/Papers/whyfp.html 。被众多老大推荐的经典论文。这篇文章出来,“黏合”的概念便广为传播。里面还有不少精彩例子,包括求解微分积分,和大小树剪枝。不是每个人都对数学感兴趣。而大小树的例子又太长。不然他们都值得细述。
[11] 刘未鹏,《你应当如何学习C++》, http://blog.csdn.net/pongba/archive/2007/05/16/1611593.aspx
[12] 我最早的实现要笨拙得多,幸好新闻组有人出手解惑: http://groups.google.com/group/comp.lang.scheme/browse_thread/thread/1fa9a460bdb3110f/9b310ada96a8d637?hl=en
[13] Simon L Payton Jones,
Implementation of Functional Programming Languages, 1987, http://research.microsoft.com/~simonpj/papers/slpj-book-1987/index.htm 规则在第7章。下面是代码对应的转换规则: flat-map f [] = [] flat-map f (x: xs) = (f x) ++ (flat-map f xs) (a) TE[[E | v<- L: Q]] = flat-map (lambda (v). TE[[E | Q]]) TE[L]
(b) TE[[E|B; Q]] = if TE[B] TE[[E|Q]] NIL
(c) TE[ [e |]] = Cons TE[E] NIL
这里E是表达式, B是返回布尔值的表达式,L是列表,Q是一个或多个生成器或B,而v表示变量。这里是一个例子:
TE( [x * x | x <- xs; x > 2])
ð flat-map (lambda x. TE([ x * x | x > 2])) xs
ð flat-map(lambda x. if (x > 2) then TE([x * x | ] ) nil) xs
ð flat-map(lambda x. if(x > 2) then (cons (x * x) nil) nil) xs
[14] Guy Lapalme,
Implementation of Lisp Comprehension Macro, http://rali.iro.umontreal.ca/Publications/urls/LapalmeLispComp.pdf, 这篇论文里用了优化过的转换规则,并且通过修改reader macro, 让生成的宏识别通用的方括号[],而不是象我们例子那用函数名list-of。不过呢,Common Lisp的宏要求我们手工完成模板中代码的替换,所以随处可见准引号`, 取引号操作符,,和去引号兼列表剥除操作符,@。相比之下,Scheme的syntax-rule就清爽多了。人叫define-syntax而不是defmacro,并非浪得虚名。
P.S., Jacky老大说这篇帖子不够生动,有妇联干部带三个表劝小夫妻不要离婚的严肃作派,并慷慨提供了范文。也一并帖在这里:
scheme!知道的明白是无数括号堆砌起来的一门语言 ,不知道还以为是schema的同门师兄弟。于是有很多同行问 ,为什么要学习传说中这样诡异的语言。我的回答往往只有一字 :爽感!(在“爽”字被用烂了的一个环境下,爽感似乎更能表达我 的那种澎湃之情!)当大家看着你噼里啪啦在键盘上敲着一行行天书 ,眼中崇敬迷离的眼神对你葱白攀生到有3,4层楼那么一个高度的 时候,是不是那脆弱的虚荣心得到了极大的高潮?爽乎 !scheme 不仅可以让你成为更优秀的程序员,教你可以写出高效美妙的程序 ,还可以帮助我们理解计算的本质。当然如果你只是做业务方面的应 用,不需要任何算法,数学计算,只是需要在一些现成的架构里面填 充一些业务流程的话,看看前面下面部分介绍就足够了 ,当别人在吹嘘显摆的时候,你还不至于以为你到了火星。当然 ,如果你对scheme充满好奇,兴趣的话,那就太棒了 ,本篇文章就是领你进入这个神奇世界的台阶,做好准备 ,我们准备起飞。 3 1975年问世的Scheme是Lisp方言,所以我们不妨先吹 吹LISP。传说中,排资论辈,LISP和FORTRAN是都是 属于古老的语言,但是fortran经常作为反面教材 ,LISP相比之下那自然是无限风光,倍受世人赞誉 。LISP拥趸们不断“发现”Lisp里简单却深刻 ,浅显而强大的特性,并应用到不同地方,取得非凡成就 。牛牵到哪里都是牛,上下纵横50年,就比如说现在红的发紫的R uby,Python,和JavaScript语言 ,它们最为人称道的功能,竟然大多源于Lisp(后面会有例子说 明)。也许John K. Foderaro这位老牛的比喻和总结最能说明Lisp的价值 :Lisp好比变色龙,高度适应环境的改变,因为它是一门 *可以编程的编程语言*。我们不仅可以用Lisp编程 ,还可以对Lisp编程i。Lisp内置的抽象方法让Lisp程 序员们身段灵活,长袖善舞。每当新的编程范式出现 ,Lisp程序员们总能快速实现相关功能,甚至做出进一步改进。 ----比如Smalltalk展示面向对象编程的潜力后 ,MIT媒体实验室的Cannon Howard便在1982年推出Flavors,一个功能丰富的 面向对象扩展。Cannon的扩展不仅实现了 当时流行的面向对象功能,还首创了多继承,多重分派 ,以及被Ruby程序员狂赞的mixini。尔后Gregor Kiczales又在集大成的CLOS里加入现在颇为眩目的面向 方面(AOP)编程方法ii。---这段如果再比较说明和LIS P的关系的话,我想那就更好了。 LISP吹捧完了后,现在再说说Scheme的传奇故事 。1958年,John McCarthy从达特茅斯搬到MIT。当时人工智能的另一奠基 人Marvin Minsky也在MIT。牛人相见,好比姚麦组合,利刃相击 ,火花耀眼。著名的MIT人工智能项目在两人领导下上马i 。但是在研究AI的过程中,McCarthy需要一门编程语言表 达他的理论模型。而当时人见人爱的图灵机只有一套笨拙的语言 ,不适合干净利落地表达复杂的递归函数,于是乎需求产生了 ,McCarthy在丘齐的lambda算子基础上顺便就设计了 Lisp,其实最初Lisp是一个纯纯的理论工具 ,用来进行程序的推导和证明。实在需要用机器验证理论了 ,研究组的老大们就手工把Lisp程序翻译成IBM 740的汇编代码,再上载到IBM 740上运行。人肉编译器们甚至热衷于编译各式Lisp程序 ,觉得跟解智力题一样好玩儿。他们还证明了可以用Lisp写出一 个通用函数eval(), 用来解释执行Lisp的表达式i。但他们光顾赞叹eval( )和元图灵机一样彪悍,且比图灵机构造出元图灵机的代码美妙 ,并没想到eval就是一个通用的Lisp解释器。幸好有天McCarthy的学生S.R. Russell灵机闪现,连夜用IBM704的机器语言实现ev al()。于是世界上第一个Lisp解释器横空出世 ,人肉编译才渐渐失传。那时真是计算机科学研究的黄金时代啊 ,人们可以一夜之间改变世界,比居委会大妈在股市一夜暴富还来得 轻快。顺便提一下,我们习以为常的条件判断语句,也是McCar thy在Lisp里发明的。而为了让函数应用没有副作用和实现函 数闭包,McCarthy的研究小组又顺便发明了垃圾收集 。这些顺便发明的产物,那一样不是现在编程语言基石 ,当时要是随便一样跺跺脚,现在的编程格局估计都要中个几百下面 目全非脚。1975年,同是MIT的Gerald Jay Sussman和Guy Steels为了研究Carl Hewitt的面向对象模型,用Lisp编写了一个玩具语言 。这个玩具语言简化了当时流行的Lisp语法,引入了词法定界 (又叫静态范围)和Continuation两大革新 。Sussman和Steels给这门语言取名Schemer ,希望它发展成像AI里著名系统Planner一样的有力工具 。可惜当时MIT用的操作系统ITS只允许最长6个字节的文件名 。Sussman和Steels不得不把Schemer的最后一 个字幕’r’去掉。Scheme问世便显露峥嵘:Sussman 和Steels很快发现Scheme的函数和Hewitt模型里 的演员(也就是我们现在所谓的对象)没有本质区别 ,连句法都基本一致。事实上,Sussman在教材 《计算机程序设计与解释》的第二章用短短几十行代码展示了一套面 向对象系统。 好了,正餐现在开始。Scheme是极度简化的语言 。他的规范文档不过47页i,浓缩的就是极品,惊讶吧 。相比另一大Lisp分支Common Lisp规范的上 千页文档或者Java规范的500来页文档,可见Scheme的 短小精悍。不过,我们可以用Scheme写出优雅犀利的程序 。Scheme规范R5RS开篇道出了Scheme的设计宗旨 :设计编程语言时不应堆砌功能,而应去掉让多余功能显得必要的弱 点和限制。Smalltalk的发明人Alan Kay在一次访谈录中提到,Lisp是编程语言中的麦克斯韦方程 组ii。这句评价用到Scheme上更为合适。Scheme甚至 让我们写出用其他语言无法写出的程序。这个时候,一般是老大们轻 蔑抛出编程语言图灵完备这种论点的时候。所以俺不妨小小地提醒一 下:理论上,理论和实践没有差别,但实际上两者差别海了去了 。不然,我们干嘛不继续用机器语言编程呢?Scheme写出的程 序用汇编/C也能实现,不过这样想的老大们最好先用汇编 /C写出一个Scheme的解释器。Sussman和Steel es用Scheme探索不同的编程模型时时,往往一周做出十来种 不同的解释器,可以旁证Scheme的简洁和灵活 。在解释是什么造就了Scheme的精练与生猛之前 ,我们先介绍一下Scheme的基本元素: