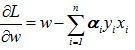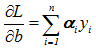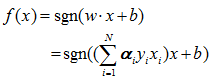机器学习(七)支持向量机svm中级篇
上一篇博文中我们得到的最后求解方程是:
接着我们将详解它的求解方法。这一步涉及到拉格朗日求解问题,有点难,建议如果想学这个问题是怎么求解的,先去好好学学拉格朗日的对偶问题求解。
一、数学基础知识复习:
这里我们先复习一下拉格朗日求解约束型最大最小值问题:用“拉格朗日乘数法”求函数f(x,y,z)在条件φ(x,y,z)=0下的极值,步骤如下:
1.做拉格朗日函数L=f(x,y,z)+λφ(x,y,z),λ称拉格朗日乘数;
2.求L分别对x,y,z,λ求偏导,并且令偏导数方程为零,得四个方程组成的方程组,然后联立方程组,可求出驻点P(x,y,z)。
如果这个实际问题的最大或最小值存在,一般说来驻点唯一,于是最值可求。接着讲一下拉格朗日对偶问题,根据上面问题构造的拉格朗日函数:
L(x,y,z,λ)=f(x,y,z)+λφ(x,y,z),
此时,我们只对未知的变量x,y,z进行求偏导并令求导的等式为零,这样我们可以得到三个方程,然而这三个方程中有四个未知数:x,y,z,λ。此时我们根据三个方程,可以把x,y,z表示成λ的函数,也就是我们可以得到x(λ),y(λ),z(λ)。最后我们把这三个方程代入原拉格朗日方程L(x,y,z,λ),可以得到关于变量λ的函数L(λ),然后上面的关于变量x,y,z的最值约束问题,这就转化成了关于变量拉格朗日乘子λ的最值问题,是就是所谓的拉格朗日对偶问题。
说的简单一点,对偶问题就是把原拉格朗日问题转换成其等价形式,以便于求解。需要注意的是,如果原拉格朗日是求解最小值,那么其对偶方程为求解最大值;反之,如果原拉格朗日求解最大值,那么其对应的对偶问题为求解最小值。
二、svm对偶问题转化
回到svm求解方程,然后我们根据上面的知识,把它转化成其对应的对偶方程。转化步骤如下:
1、构建拉格朗日函数:
2、对拉格朗日函数求偏导:
![]() (这个公式告诉我们所有的数据点的分类符号与拉格朗日乘子乘积和为0)。
(这个公式告诉我们所有的数据点的分类符号与拉格朗日乘子乘积和为0)。
在这里我们可以知道,如果拉格朗日乘子α已经求得,那么我们就可以根据上面的公式得:
这里请记住这个公式,因为这个公式,将作为后续计算拉格朗日乘子是否满足KKT条件的第一步。
4、回待入拉格朗日函数,并整理得:
这就是我们最后的转化结果。因此接着我们的目的便是要研究这个方程怎么继续求解。
三、松弛因子
由于在给定的训练样本中,总存在噪声,因为人工标号,有的训练数据标号甚至是错误的。还有以上的推导过程我们都是以数据100%线性可分为假设,进行推导的。如果我们采用硬约束的方法,很容易引起过拟合。因此我们需要引入所谓的松弛变量,来允许有些数据点可以存在较小的误差。因此svm算法的求解方程变为:
参考文献:http://blog.csdn.net/zouxy09/article/details/17291543