UVa OJ 122 - Trees on the level (分层树)

Background
背景

Trees are fundamental in many branches of computer science. Current state-of-the art parallel computers such as Thinking Machines' CM-5 are based on fat trees. Quad- and octal-trees are fundamental to many algorithms in computer graphics.
各种树（数据结构）是许多计算机分支学科的基础。当下最快的并行计算机——比如思维机CM-5——就是建立在一种称之为“胖树”（fat trees）的架构上的。而四叉树和八叉树又是许多计算机图形学算法的基础。

This problem involves building and traversing binary trees.
本问题是关于建立和遍例二叉树的。

 

The Problem
问题

Given a sequence of binary trees, you are to write a program that prints a level-order traversal of each tree. In this problem each node of a binary tree contains a positive integer and all binary trees have have fewer than 256 nodes.
给定一个二叉树序列，你要写一个程序将每棵树按层序访问并打印出来。在这个问题中，二叉树的每个节都值都为正整数，且每棵树的节点数都小于256。

In a level-order traversal of a tree, the data in all nodes at a given level are printed in left-to-right order and all nodes at level k are printed before all nodes at level k+1.
在层序遍例一个树时，指定行中所有的结点应按照从左至右的顺序打印，并且在第k行打印完之后才能打印第k+1行。

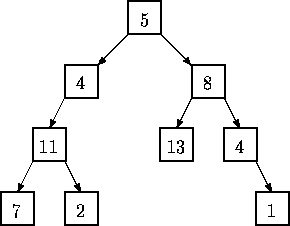
For example, a level order traversal of the tree
比如，按层序遍例下面的树的结果是：

 

 

is: 5, 4, 8, 11, 13, 4, 7, 2, 1.

In this problem a binary tree is specified by a sequence of pairs (n,s) where n is the value at the node whose path from the root is given by the string s. A path is given be a sequence of L's and R's where L indicates a left branch and R indicates a right branch. In the tree diagrammed above, the node containing 13 is specified by (13,RL), and the node containing 2 is specified by (2,LLR). The root node is specified by (5,) where the empty string indicates the path from the root to itself. A binary tree is considered to be completely specified if every node on all root-to-node paths in the tree is given a value exactly once.
在本问题中，二叉树是由一系列的二元组(n, s)给出的，其中n是节点的值，s是由根到该节点的路径字符串。路径字符串由一系列的“L”和“R”组成，L代表左子树，R代表右子树。在上图所示二叉树中，值为13的节点由(13, RL)表示，值为2的节点由(2, LLR)表示。根节点由(5,)表示，其中空的路径字符串表示的路径就是由根到根。当一个二叉树中，所有从根到节点（已给出的）的路径上的所有的节点都已给出且只给出一次，那么这个二叉树就认为是完整的定义。

 

The Input
输入

The input is a sequence of binary trees specified as described above. Each tree in a sequence consists of several pairs (n,s) as described above separated by whitespace. The last entry in each tree is (). No whitespace appears between left and right parentheses.

输入是一组按照上文所述给出的二叉树定义。序列中的每棵树都包含数个二元组(n, s)，分别以空格隔开。每棵树的最后是()。所有的左右括号中间都不存在空格。

All nodes contain a positive integer. Every tree in the input will consist of at least one node and no more than 256 nodes. Input is terminated by end-of-file.
所有节点的值都为正整数。输入的每棵树都包括至少一个节点，且不会超过256个节点。输入由EOF表示结束。

The Output
输出

For each completely specified binary tree in the input file, the level order traversal of that tree should be printed. If a tree is not completely specified, i.e., some node in the tree is NOT given a value or a node is given a value more than once, then the string "not complete" should be printed.
对于输入的每行完整定义的二叉树，都要按层序遍例并打印。如果一棵树没有完整的定义，即一些节点没有给出其值，或是一个节点重复给出，则应该打印出字符串“not complete”。

 

Sample Input
输入示例

(11,LL) (7,LLL) (8,R)
(5,) (4,L) (13,RL) (2,LLR) (1,RRR) (4,RR) ()
(3,L) (4,R) ()

 

Sample Output
输出示例

5 4 8 11 13 4 7 2 1
not complete

 

Analysis
分析

这道是一个直接的二叉树广度遍例问题，按照题目要求来处理就可以了。要注意所给的二元组可能没有数字，也可能没有路径串，这些情况都要很仔细的处理。此外，重复给出的节点以及未给出的节点都算输入错误，全部要输出not complete。在提交你的解答前请务必自己造几个这样的特殊情况检验一下，否则很可能WA。

此外，顺便提一下广度遍例的方法。需要建立一个链表（为加快插入和删除操作）来存储每一层的节点。先将根节点加入链表，然后开始依次（从左至右）遍例链表中的每一个节点。遇到一个不为空的节点，则输出之并将其删除，然后将它的两个子节点在原位置上插入，再向右继续下一个节点。一直到该层所有节点遍例结束，此时链表中的节点即为下一层的所有节点，再从头开始遍例即可。如此往复，一直到链表为空，则说明整棵树遍例结束。算法时间复杂度为O(n)。

Solution
解答

#include <iostream>
#include <list>
#include <string>
#include <sstream>
using namespace std;
//节点结构体，存储节点的值及左右子节点
struct NODE {int nVal; NODE *pL; NODE *pR;}
//NullNode为空节点标本
const NullNode = {0, 0, 0};
//删除树
void DeleteTree(NODE *pPar) {
	if (pPar != NULL) {
		//深度遍例删除左右子节点
		DeleteTree(pPar->pL), DeleteTree(pPar->pR);
	}
	delete pPar;
}
//为树增加节点
NODE* AddChild(NODE *pPar, int nVal, const char *pPath) {
	//如果父为空，则建立父节点
	if (pPar == 0) {
		pPar = new NODE(NullNode);
	}
	//根据当前路径字符串做不同操作
	switch (*pPath) {
	//遇到右括号，说明路径结束，为当前父节点赋值
	case ')': pPar->nVal = (pPar->nVal == 0 && nVal != 0) ? nVal : -1; break;
	//继续建立左/右子节点
	case 'L': pPar->pL = AddChild(pPar->pL, nVal, pPath + 1); break;
	case 'R': pPar->pR = AddChild(pPar->pR, nVal, pPath + 1); break;
	}
	return pPar;
}
//主函数
int main(void) {
	//树的根结点
	NODE *pRoot = 0;
	//循环处理输入的每一个节点数据
	for (string strToken; cin >> strToken;) {
		//获得节点数据字符串指针
		const char *pStr = strToken.c_str();
		int nLen = strToken.length(), nVal = 0;
		//如果第二个字符不是右括号，则添加节点后继续输入
		if (pStr[1] != ')') {
			//将字符串转为数字
			for (; isdigit(*++pStr); nVal = nVal * 10 + *pStr - '0');
			if (*pStr != ',') while(true);
			//在树中添加该节点
			pRoot = AddChild(pRoot, nVal, ++pStr);
			continue;
		} //如果第二字符是右括号，说明一棵树输入结束，进行遍例
		list<NODE*> Level(1, pRoot);
		stringstream ssResult;
		//依次遍例每一层。用Level存储一层的节点，Level非空则继续遍例
		for (list<NODE*>::iterator i = Level.begin(); !Level.empty();
			//如果一层遍例结束，则回到起点
			i = (i == Level.end() ? Level.begin() : i)) {
			//移除当前节点
			NODE *pTemp = *i;
			i = Level.erase(i);
			//如果该节点为空，则直接继续进行下一个节点
			if (pTemp == 0) {
				continue;
			}//否则在原位置上增加子节点
			//如果该节点的值小于或等于0，说明其重复定义或未定义
			if (pTemp->nVal <= 0) {
				//清空数据，返回错误。
				Level.clear();
				ssResult.str("");
				break;
			}//正确的结点
			//输入其值，并在原位置上插入其子节点
			ssResult << pTemp->nVal << ' ';
			i = Level.insert(i, pTemp->pL), ++i;
			i = Level.insert(i, pTemp->pR), ++i;
		}
		//删除原树，避免内存泄露。
		DeleteTree(pRoot);
		pRoot = 0;
		strToken = ssResult.str();
		//如果结果为空，说明所给数据有错
		if (strToken.empty()) {
			strToken = "not complete";
		} //对于正确结果要去掉最后的一个空格
		else {
			strToken.erase(strToken.end() - 1);
		}
		//输出结果
		cout << strToken << endl;
	}
	return 0;
}