编译原理之文法二

    1956年，Noam Chomsky根据对产生式所施加限制的不同行，把分发分为了四种类型，并定义了相应的四类形式语言，如下：

文法类型	产生式限制	文法产生的语言
0型文法	α→β 其中α、β属于(VTUVN)*，且α长度不为0	0型语言
1型文法	α→β 其中α、β属于(VTUVN)*，且α的长度小于β的长度	1型语言/上下文有关语言
2型文法	A→β A属于VN，β属于(VTUVN)*	2型语言/上下文无关语言
3型文法	A→α|αB（右线性）或A→α|Bα（左线性） 其中A,B属于VN，α属于VT或空集	3型语言/正规语言

文法限制

    0型到3型文法，限制逐步增多，且呈包含关系。

0型文法

    0型文法也称为短语文法。一个很重要的结论是，0型文法的能力相当于图灵机。任何0型语言都是递归可枚举的；反之，递归可枚举集必定是一个0型语言。

    0型文法是限制最少的一个文法，产生式只需满足左部包含一个非终结符（大写）即可，例如：A0→A0 , A1→B。

1型文法

    1型文法又称为上下文有关文法，在0型文法的基础上，新加一条限制：产生式右部长度大于等于左部长度，例外情况是 S→ε，即推导出来的是空集。例如0A0→011000。

2型文法

    2型文法又称为上下文无关文法，在1型文法的基础上继续添加限制：产生式左部都是非终结符。例如：A→ab，AB→BAc。

3型文法

    3型文法是最严格的一种文法，也称之为正规文法，在2型文法的基础上继续添加限制：即其产生式的右部至多有两个符号，而且具有下面形式之一: A →a ，A →aB， 其中A,B∈VN ，a∈VT 。注意3型文法只能是左线性或右线性，不能二者同时有，左线性和右线性指的是产生式右部，非终结符所在位置是左还是右。

    注意不同的文法可能产生相同的语言。

推导树

     如果所有的终端结点都是与终结符关联的，每棵推导树的终端结点自左至右所构成的字符串是文法G的一个句型，则该字符串是文法G的一个句子，此时该推导树是完全推导树。

    一棵语法树应具有以下特征：
    1．每个结点都有一个标记，此标记是V的一个符号：
    2．根的标记是S:
    3．若一结点n至少有一个它自己除外的子孙，并且有标记A，则A肯定在VN中；
    4.   加果结点n的直接子孙，从左到右的次序是结点n1,n2……nk，其标记分别是：A1,A2，…，Ak，那么A一＞A1,A2…Ak，一定是p中的一个产生式。

    现有文法G=（{a,b}，{S,A},S,P），其中：S→aAS|a,A→SbA|SS|ba，构造aabAa相对应的推导树。
    由产生式可以得到VT={a,b}，VN={S,A}，分解出S→aAS|a，即S→aAS，S→a，A→SbA|SS|ba，即A→SbA，A→SS，A→ba，根据分解出的产生式，可以得到推导树：

        

正规式

        正规式又叫正则表达式，是一种表示正规级的工具，每个正规式对应一个正规文法（3型文法）。

        正规文法转为正规式

        

        规则1：由A→xB，B→y得到：A→xB→xy
        规则2：由A→xA|y，可知：A→xA，A→y，依次往下推A→xA→x^2A→x^3A……→x*A→x*y
        规则3：A→x,A→y简写成A=x|y

        例如语言L={a^mb^n|m>=0,n>=1}的正规式：因为*代表0到多个、m的值为大于等于0，所以a^m可以表示为a*，而n大于等于1，可以使用bb*来表示，所以语言L的正规式可以表示为a*bb*。

有限自动机

         有限自动机是具有离散输入和输出的一种系统数学模型。有限自动机拥有有限数量的状态，每个状态可以迁移到零个或多个状态，输入字串决定执行哪个状态的迁移。有限自动机可以记做一个五元组：M=(Q,Σ,δ,q0,F)，其中：

• 有穷状态集合 Q 
• 有穷输入字母表 Σ，其中的每个元素称为一个输入符号
• 转移函数 δ: Q × Σ -> 2Q，是一个Q与Σ的笛卡尔积到Q的单值映射
• 初始状态 q0，q0属于Q
• 终结状态集合 F，F 包含于 Q 

    例如M=({S,A,B，C，f},{1,0},S,{f},δ)，它的δ为：δ(S,0)=B,δ(S,1)=A,δ(A,0)=f,δ(A,1)=C,δ(B,0)=C,δ(B,1)=f ,δ(C,0)=f,δ(C,1)=f。对应的状态转换图为：

        

    这个有限自动机可以解释为：从S出发，到f结束，S接受1转到A状态，S接受0转到B状态……其中如果从S到f接受的字符拼接的串w全部来自字母表Σ，则w被此自动机识别，M能识别的字符串w的集合成为M所能识别的语言。

    有限自动机又可以分为确定的有限自动机和不确定的有限自动机，区别在于不确定有限自动机的起始状态和转换到的状态时不确定的。有限自动机位于编译中的词法分析阶段，它的作用是用来判断状态的转换，及执行相关的语义动作，例如当识别到一个标识符时，向符号表中添加该标识符，并且向语法分析程序输送该标识符的单词。

正规式与有限自动机的转换

        每一个正规式R都对应一个有限自动机M，M能接受的语言就是正规式的值。

        定义初始状态S和结束状态f，S经过R到f，组成有向图：

             

            转换规则为：

            

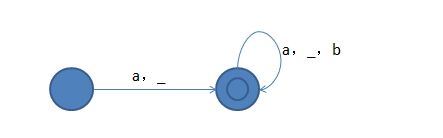
            例如C中标识符的定义只能是以“_”和字母开头，有字母和数字组成，假设a代表字母{a,A,b,B,……}，b代表数字{0……9}，那么C能接受的标识符的正规式可以为：

(_|a)(_|a|b)*

        此正规式对应的有限自动机图为：

         

        关于文法、正规式、自动优先级先说到这里。