虹膜识别(五):虹膜分割与图像归一化
(一)进一步分割
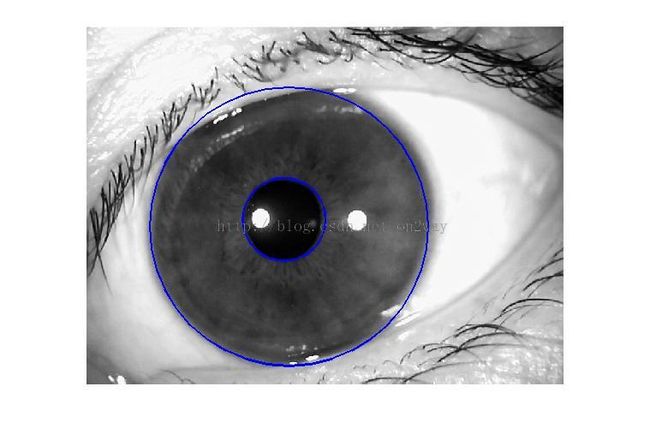
上面已经得到了关于分割区域的虹膜部分如下图所示:
内外圆之间的部分认为是要进行识别的部分。
该图的大小为600*800,内外圆的参数前面计算过,这里再给一遍:
mean_circle_in =[324 ; 332 ; 69];
mean_circle_out =[336 ; 340 ; 233];
参数形式为
% mean_circle : 圆心横坐标
% mean_circle :圆心纵坐标
% mean_circle :圆的半径
现在去掉内外圆之外的部分,原理是直接对所有的像素点依次进行检验,比较它们到圆心的距离与所给圆的半径的大小,据此划分内外点。程序如下:
function img_new = wipeout(img,mean_circle_in,mean_circle_out)
%------------------------------输入参数-----------------------------
% img : 原始图像
% mean_circle_in: 分割内圆的参数
% mean_circle_out:分割外圆的参数
% 参数形式: mean_circle(1) : 圆心横坐标
% mean_circle(2) :圆心纵坐标
% mean_circle(3) :圆的半径
%
%------------------------------输出参数-----------------------------------
% img_new:新分割图像
%[600 800]
[line,row]=size(img); %取大小
for i = 1:line
for j = 1:row %计算距离
dis = sqrt((i-mean_circle_out(1)).^2+(j-mean_circle_out(2)).^2);
if dis > mean_circle_out(3) %比较距离大小:外圆取大于
img(i,j) = 255;
end
end
end
for i = 1:line
for j = 1:row %计算距离
dis1 = sqrt((i-mean_circle_in(1)).^2+(j-mean_circle_in(2)).^2);
if dis1 < mean_circle_in(3) %比较距离大小:内圆取小于
img(i,j) = 255;
end
end
end
img_new = img;
对最初始的灰度图像调用该函数并显示出来如下:
img_new = wipeout(img,mean_circle_in,mean_circle_out);imshow(img_new)
(二)关于图像归一化
图像归一化是指对图像进行了一系列标准的处理变换,使之变换为一固定标准形式的过程,该标准图像称作归一化图像。
我们这里的归一化是指要把圆环状的图像归一化为矩形的图像,这样既可以压缩图像的大小(去掉圆饼以外的白色不需要的像素)又便于后续的特征提取或者识别操作,处理的原理很简单,想想一下,就是把这个圆饼状从某处切开,然后分别往两边一拉就成矩形状了,当然这个过程会使得图像略有点变形,变形的部分我们用它邻近的像素点代替就可以了,比较这个影响不是很大。
算法上实现也很简单,重点是找到坐标的对应关系,如下图所示:
直观图为:
依此编写坐标变换算法:
function [img_rec,M,N] = circle2rectangle(img,mean_circle_in,gama_in,gama_out)
%------------------------------输入参数-----------------------------
%圆参数 mean_circle_in:
% mean_circle_in(1) : 圆心横坐标
% mean_circle_in(2) :圆心纵坐标
% mean_circle_in(3) :圆的半径
%
% gama_in:归一化上边缘范围 一般半径的1.4倍较好
% gama_out:归一化下边缘范围 一般半径的2.7倍较好
%-------------------------------------------------------------------
%------------------------------输出参数-----------------------------
% img_rec: 归一化图像---》圆形转换的矩阵图
% M,N 转换的矩阵图的 -- 行列的大小
%
%-------------------------------------------------------------------
R_in = round(mean_circle_in(3)*gama_in); %限制半径
R_out = round(mean_circle_in(3)*gama_out);
%转换的列数
%N = 800;
N = round(pi*(R_out+R_in));
%转换的行数
% M = 100;
M = round(R_out-R_in);
alpha = 2*pi/N;
for k = 1:N
%内外圆的坐标矩阵
point_A_x(1,k) = mean_circle_in(1) + R_in*cos(k*alpha);
point_A_y(1,k) = mean_circle_in(2) + R_in*sin(k*alpha);
point_B_x(1,k) = mean_circle_in(1) + R_out*cos(k*alpha);
point_B_y(1,k) = mean_circle_in(2) + R_out*sin(k*alpha);
end
% figure,plot(point_A_x);
%重构要求的M*N矩阵坐标
for i = 1:M
point_x(i,:) = round(point_A_x(1,:) + (point_B_x(1,:) - point_A_x(1,:))*i/M) ;
point_y(i,:) = round(point_A_y(1,:) + (point_B_y(1,:) - point_A_y(1,:))*i/M) ;
end
for i = 1:M %映射关系
for j = 1:N
img_rec(i,j) = img(point_x(i,j),point_y(i,j));
end
end
有了该函数,可以直接对圆心进行操作了,大概确定相应的参数后即可以实现了,例如选的一定的半径范围如下:
>> [img_rec,M,N] = circle2rectangle(img,mean_circle_in,1.4,3);
>> imshow(img_rec)
得到结果为:
>> M,N
M =110;N =955
同时新图像的大小也可以看到,相比原图像小了很多。为后续的处理提供了很大的方便。