图像分割之图割工具箱GCO3.0的使用（二）

一）：之前

之前在博客
matlab实现图割算法中的最大流最小割Max-flow/min-cut问题
中我们讲到了关于图中求取最小割最大流的一个软件包，并简单介绍了它在图像分割中的应用，但是并没有深入给出具体实例，这里我们再在最小割最大流原理基础上介绍同一个研究所出的另一种集成的软件包gco-v3.0，这个软件包则是直接可以对图像进行分割操作的，达到可以观测的效果。
关于软件包gco-v3.0的下载地址，同样在网址为：http://vision.csd.uwo.ca/code/在这里找到对应的内容即可；

二）：准备

好了下载好的工具箱解压，里面会有一些c编写的代码以及另一个matlab版文件夹，这里说一下，同样是使用matlab来进行后面的所有操作（在使用之前需要编译一下成matlab可用的文件，程序里面有）。那么文件夹里面的文件正常的话就如下：
乍一看，好多函数呀，不要着急，如果不了解要一个个看确实费劲，但是每个仔细看了以后就会发现其实每个都有用途的，后面也会对每个函数进行讲解说明的，以加快初学者学习的进度。

三）：理解

好了现在我们来回味一下关于基础的图割算法需要哪些部分，连基本概念都不知道的建议去看一下上一篇文章：
matlab实现图割算法中的最大流最小割Max-flow/min-cut问题
看完后起码知道在进行图割算法操作的时候，一些必备的项，矩阵等等都知道，比如关于一个待分割图的数据项Datacost（点与源汇点（类点）之间的权值），平滑项Smoothcost（点与点之间的权值），标签Labeling（所有点各属于哪一个类），等等。借用上篇文章的图，比如下列的两分割问题：

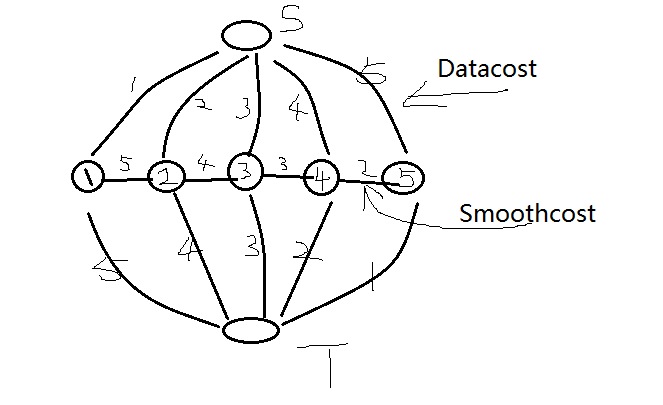
当然，正常的一个图像可能不是两分割问题，可能存在多分割问题，这个时候类的点数（S，T）可能就不是两个了，可能就是多个，把S，T都统一为类L的话，那么一个图就可以分割为如下：

大概先简化为这样吧，画的比较丑，图中有分的类L（L1，L2…）,点数N（n1,n2,…）,以及所有的边的权值（两类不同的边的权值吧），datacost应该好理解，就是每一个点都会与所有的类有一个权值，这个值越大就说明它越属于这一类，smoothcost就是点与点之间的权值，这里画的是一维的情况，表示的是二维的关系，什么意思呢，想想一幅图是m*n的图是什么样子的，就是m*n的像素点吧，把每个像素点看成这里的一个点，假设现在是3*3的图吧，像素值都在0-255之间，那么你在matlab下看到的图像就是这样的：

这里我们只认为每个点与它附近的4连通区域有关（也有8连通区域），并且他们之间的权值（也就是smoothcost）简单的话就把他们之间的像素差值当做cost，如上图所示。这样看来这是个二维的点阵，那么如何应用到上述的图呢?这里我们就要在认识上转化为一维的了，把这些点从1-9依次排开，然后我们看到点1与2和4相连，点2和1,3,5相连，点3和2,6相连等等，而连接的权值就是相应的像素差绝对值，那么对于没有相连的，比如点1与3,5,6,7,8,9这些点怎么办了，我们也可以认为他们相连，只不过连接的权值为0而已；这样是不是就出来了smoothcost矩阵了，而且大小为[m*n,m*n],也可以看到，这个矩阵是一个稀疏矩阵，也就是有（大概）80%的点为0，这要是都写出来是非常占内存，所以在后面处理的时候会看到，这个矩阵是需要用稀疏矩阵来生成的，matlab是有对应函数去生成的，比如下面这个：

%matlab函数生成稀疏矩阵（这么做的速度最快）
neighb = spconvert(all);

图形化这个二维矩阵到一维就是这样的：

对于边权值为0的边就没有画出来，这样一个图像就可以用一维表示出来，就可以用上述图割方法了。
当然还有很多问题，比如说有多少个类L，每个点到各个类之间的权值为多少，这些都会在求解问题的时候遇到。

四）：再理解

学习图割分割算法之前，看看几篇专业研究这方面的文献是很有必要的，比如：
http://wenku.baidu.com/link?url=r0UJHR5stIvnfYiRa5cbDqfY-icr6OmqV3afUCCQkcou6xyrqlDwKCdllWgUUBtdcJBoZcs9DeRSTqLUJ-Eih6Xi6MNmOP_I9EuAqr3pWVO

http://wenku.baidu.com/link?url=qMhM4Lbz24gupBNVOz0aSD7zmoqLKvzYRPwoxWUluvIXcqeIKzqrQ9SBCeInGX8oUFQdFzJpd9Vi0bfv4-2-OXGTP97teUQMlkVMvG73Pba
这两篇文献是非常经典的。图割分割算法在有了上述工具箱之后，只需要（主要）确定了上述说到的smoothcost和datacost就可以运行了。下面来谈谈工具箱中函数的具体用法：

4.1）创建目标体GCO_Create

函数用法：

%%--- 创建一个优化目标体 Handle %      Handle = GCO_Create(NumSites,NumLabels)
%      NumSites：所有点数目； NumLabels：所有标签数

这个函数中，在确定了待分割图像后，NumSites就是所有点个数（m*n），NumLabels是要分类的类别数（也应该知道）。

4.2）设定分类标签GCO_SetLabeling

%%----为当前目标体设置标签 %    GCO_SetLabeling(Handle,Labeling)，其中Labeling为1*Numsites的向量；
%    也就是为目标体中每个点设置一个标签

这个函数就是给所有点设置一个分类标签，Labeling就是设置的标签，可能有人会说，标签不是我们最终要求解的吗，为什么自己可以设置，确实，我们的目的就是求解分类标签，但是是更好的分类标签，这个分类标签可以是预分类的标签，比如你可以在分类前使用kmeans预分割一下，把这个预分割标签设置进去，kmeans预分割还有一个用处就是找到初始的各个类中心。

4.3）重头戏之设置GCO_SetDataCost

datacost上述说到，所有点与每个类（中心）之间的权值大小，越小，说明该点越属于这一类，反之越大越不属于。函数说明：

%%------为每个点设置 datacost % 用法：GCO_SetDataCost(Handle,DataCost)
%  DataCost：大小为 NumLabels-by-NumSites ：类标签数m*总数据点数           n  接受矩阵为：n*m
%  其中每个DataCost(k,i)表示类标签k到点i的cost
%  SetDataCost函数可以反复调用；

很显然，在使用之前，你需要做的就是把DataCost求出来，然后直接设置进去，矩阵大小在上面也可以看到，注意总点数n是图像像素点的总像素点数。那么怎么去确定这个矩阵就是算法的好坏了。

4.4）重头戏之设置GCO_SetNeighbors

设置完点与类中心的权值，再来设置点与点之间的边权值，认为每个点只与附近的四领域或者八领域内的几个点有边权值，而与其他所有点边权值都为0，函数说明：

%%-----设置Neighbors之间的权值 %为所有点sites两两之间设置一个权值，从而决定哪些点是相邻的
%   使用：GCO_SetNeighbors(Handle,Weights)
%        Weights是一个NumSites-by-NumSites矩阵
%        这里：Weights(i,j) > 0就表明点i与j是相邻的
%        如果Weights是一个0-1矩阵，那么smooth costs项就是一个空间不变量
%注意：只会访问 Weights为上三角矩阵，因为矩阵图边与边之间是一个无向图

可以看到函数需要一个矩阵Weights，这个矩阵一般情况下非常大，如果是100*100的图像，那么这个矩阵就是10000*10000的，通常情况下我们是需要用稀疏矩阵来表示的，因为这个矩阵中80%以上元素为0。对于不为0的权值大小也是算法需要构造的地方。

4.5）其他设置GCO_SetSmoothCost

这个函数实际上是辅助上面那个函数GCO_SetNeighbors的，函数说明：

%%-------设置SmoothCost项 %    使用： GCO_SetSmoothCost(Handle,SmoothCost)
%           其中SmoothCost为一个NumLabels-by-NumLabels矩阵
%  对任意一个SmoothCost(k,p),如果一个邻域内存在类k与类p,表示类标签k与类标签p之间的在无权值情况下的cost；
%  而邻域内的两个点i与j，他们之间的实际带权值的cost是：Weights(i,j)*SmoothCost(k,p)；
%  空间变化上的权值是由GCO_SetNeighbors指定的；
%  如果不调用SetSmoothCost函数的话，就是一个默认的Potts模型
%       Potts模型表示的是：如果两个类k==p，那么SmoothCost(k,p)=0；认为是同类，否则值为1；

在这个工具箱中，程序所运行的实际点与点之间的权值大小其实是Weights(i,j)*
SmoothCost(k,p)；正常情况下我们用Weights(i,j)就是了，所以在不需要SmoothCost的时候，我们采用默认的Potts模型。

4.6）工具箱的运行算法：GCO_Expansion、 GCO_ExpandOnAlpha、GCO_Swap

在所有设置完成后选择一种图割算法就可以得到新的分割结果，这几种算法在前面的外文文献中都有详细的介绍。

4.6.1：GCO_Expansion函数说明：

%%-----对目标体进行alpha-expansion算法操作：返回寻找的最小能量Energy %  方式一： GCO_Expansion(Handle)，运行a-膨胀最小化当前能量--直到收敛
%  方式二： GCO_Expansion(Handle,MaxIter)     
%          加入一个迭代运行次数：MaxIter： 该算法在迭代MaxIter次后还没有找到最小能量也停止
% note： 1）：当前目标体的标签可以通过函数GCO_GetLabeling获取；
%        2）：膨胀算法中，标签膨胀的顺序可以通过函数GCO_SetLabelOrder来规定；
%        3）：如果GCO_SetNeighbors没有调用过，也就是说目标体Handle中没有smoothness项
%             这个时候，膨胀算法将会使用内部的greedy算法，不进行图割；

4.6.2：GCO_ExpandOnAlpha函数说明：

这个函数只是对其中的某一类标签进行膨胀计算，

%%----单独对目标体进行alpha-expansion 步骤 %       GCO_ExpandOnAlpha(Handle,Alpha)
%          Alpha：需要进行膨胀操作的类标签
4.6.3：GCO_Swap函数说明：
%%-----对目标体进行alpha-beta-swap算法操作：返回寻找的最小能量Energy %  方式一： GCO_Expansion(Handle)，运行alpha-beta-swap最小化当前能量--直到收敛
%  方式二： GCO_Expansion(Handle,MaxIter)     
%          加入一个迭代运行次数：MaxIter： 该算法在迭代MaxIter次后还没有找到最小能量也停止
% note： 1）：当前目标体的标签可以通过函数GCO_GetLabeling获取；
%        2）：膨胀算法中，标签膨胀的顺序可以通过函数GCO_SetLabelOrder来规定；
%        3）：无论是label costs还是sparse data costs都是在当前alpha-beta-swap算法下实现的

4.7）获得运算结果的标签GCO_GetLabeling

该函数直接运行后可以得到当前程序对于分割结果的标签，函数说明：

%%----获取当前目标体的类标签 %    用法：
%       1）：Labeling = GCO_GetLabeling(Handle)返回整个目标体的标签，列向量标签；
%       2）：Labeling = GCO_GetLabeling(Handle,i)得到具体某个点的标签；
%       3）：Labeling = GCO_GetLabeling(Handle,i,count)得到点i到i后面count个点的标签；

4.8）计算运算结果的能量GCO_ComputeEnergy

图割算法是以能量函数来作为衡量结果好坏的，图割的能量函数中主要包括3部分的能量：数据项的能量、平滑项的能量以及标签的能量。这些能量其实就是切割的边权值之和，前面介绍过。至于标签的能量，是衡量不同类之间的一种能量，正常情况下，你不去设置它也不会有，详细的可以参考上述文献。关于这个函数的说明：

%%--- 计算能量函数： %     两种方式：一）： E = GCO_ComputeEnergy(Handle) 
%                    返回当前标签下的总能量E
%              二）：[E D S L] = GCO_ComputeEnergy(Handle)
%                   返回总能量E  各部分的能量 

4.9）多余的小函数GCO_Delete

该函数为释放内存的函数，在程序运行完后加在后面与利于系统释放内存。

至此该工具箱里面的主要函数都讲解完毕，那些函数说明其实就是对应函数里面的英文说明帮助翻译过来的，还有些小函数没有用到，也就没有翻译，也都有说明。在下一次将会把这个工具箱用在一个实例上实验实验。