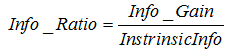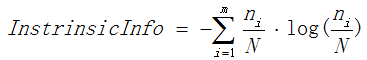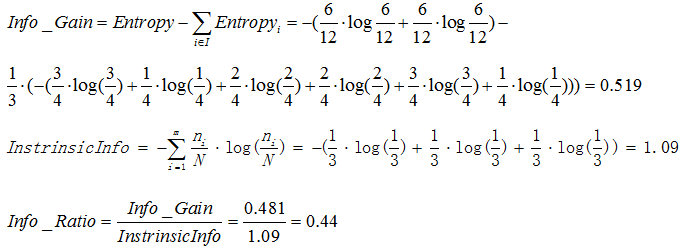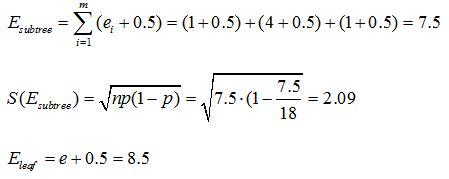决策树系列(四)——C4.5
预备知识:决策树、ID3
如上一篇文章所述,ID3方法主要有几个缺点:一是采用信息增益进行数据分裂,准确性不如信息增益率;二是不能对连续数据进行处理,只能通过连续数据离散化进行处理;三是没有采用剪枝的策略,决策树的结构可能会过于复杂,可能会出现过拟合的情况。
C4.5在ID3的基础上对上述三个方面进行了相应的改进:
a) C4.5对节点进行分裂时采用信息增益率作为分裂的依据;
b) 能够对连续数据进行处理;
c) C4.5采用剪枝的策略,对完全生长的决策树进行剪枝处理,一定程度上降低过拟合的影响。
1.采用信息增益率作为分裂的依据
信息增益率的计算公式为:
其中![]() 表示信息增益,
表示信息增益,![]() 表示分裂子节点数据量的信息增益,计算公式为:
表示分裂子节点数据量的信息增益,计算公式为:
其中m表示节点的数量,Ni表示第i个节点的数据量,N表示父亲节点的数据量,说白了,![]() 其实是分裂节点的熵。
其实是分裂节点的熵。
信息增益率越大,说明分裂的效果越好。
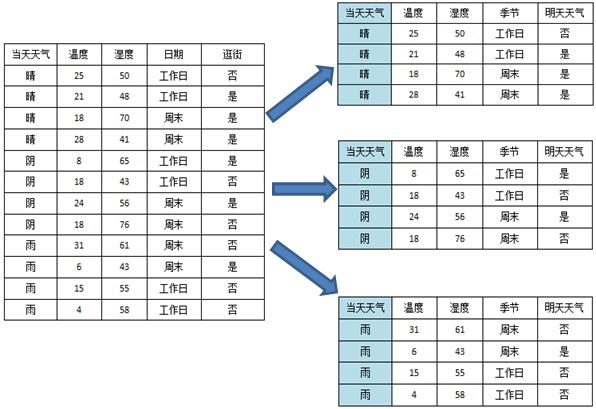
以一个实际的例子说明C4.5如何通过信息增益率选择分裂的属性:
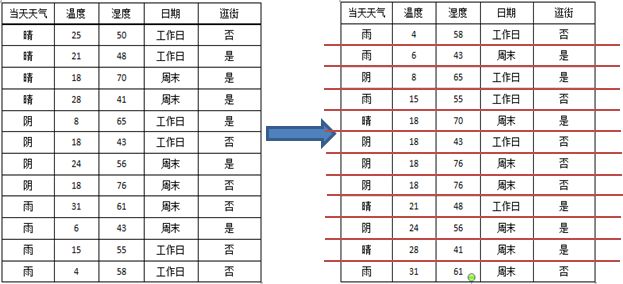
表1 原始数据表
| 当天天气 |
温度 |
湿度 |
日期 |
逛街 |
| 晴 |
25 |
50 |
工作日 |
否 |
| 晴 |
21 |
48 |
工作日 |
是 |
| 晴 |
18 |
70 |
周末 |
是 |
| 晴 |
28 |
41 |
周末 |
是 |
| 阴 |
8 |
65 |
工作日 |
是 |
| 阴 |
18 |
43 |
工作日 |
否 |
| 阴 |
24 |
56 |
周末 |
是 |
| 阴 |
18 |
76 |
周末 |
否 |
| 雨 |
31 |
61 |
周末 |
否 |
| 雨 |
6 |
43 |
周末 |
是 |
| 雨 |
15 |
55 |
工作日 |
否 |
| 雨 |
4 |
58 |
工作日 |
否 |
以当天天气为例:
一共有三个属性值,晴、阴、雨,一共分裂成三个子节点。
根据上述公式,可以计算信息增益率如下:
所以使用天气属性进行分裂可以得到信息增益率0.44。
2.对连续型属性进行处理
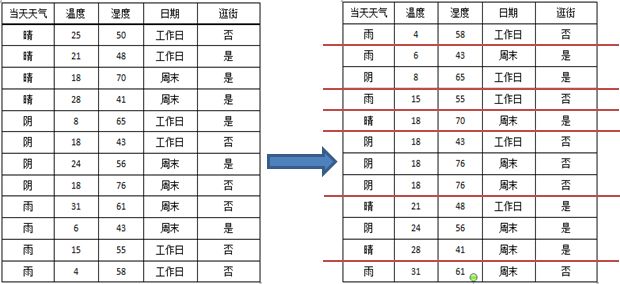
C4.5处理离散型属性的方式与ID3一致,新增对连续型属性的处理。处理方式是先根据连续型属性进行排序,然后采用一刀切的方式将数据砍成两半。
那么如何选择切割点呢?很简单,直接计算每一个切割点切割后的信息增益,然后选择使分裂效果最优的切割点。以温度为例:
从上图可以看出,理论上来讲,N条数据就有N-1个切割点,为了选取最优的切割垫,要计算按每一次切割的信息增益,计算量是比较大的,那么有没有简化的方法呢?有,注意到,其实有些切割点是很明显可以排除的。比如说上图右侧的第2条和第3条记录,两者的类标签(逛街)都是“是”,如果从这里切割的话,就将两个本来相同的类分开了,肯定不会比将他们归为一类的切分方法好,因此,可以通过去除前后两个类标签相同的切割点以简化计算的复杂度,如下图所示:
从图中可以看出,最终切割点的数目从原来的11个减少到现在的6个,降低了计算的复杂度。
确定了分割点之后,接下来就是选择最优的分割点了,注意,对连续型属性是采用信息增益进行内部择优的,因为如果使用信息增益率进行分裂会出现倾向于选择分割前后两个节点数据量相差最大的分割点,为了避免这种情况,选择信息增益选择分割点。选择了最优的分割点之后,再计算信息增益率跟其他的属性进行比较,确定最优的分裂属性。
3. 剪枝
决策树只已经提到,剪枝是在完全生长的决策树的基础上,对生长后分类效果不佳的子树进行修剪,减小决策树的复杂度,降低过拟合的影响。
C4.5采用悲观剪枝方法(PEP)。悲观剪枝认为如果决策树的精度在剪枝前后没有影响的话,则进行剪枝。怎样才算是没有影响?如果剪枝后的误差小于剪枝前经度的上限,则说明剪枝后的效果与更佳,此时需要子树进行剪枝操作。
进行剪枝必须满足的条件:
![]()
其中:
![]() 表示子树的误差;
表示子树的误差;
![]() 表示叶子节点的误差;
表示叶子节点的误差;
令子树误差的经度满足二项分布,根据二项分布的性质,![]() ,
,![]() ,其中
,其中![]() ,N为子树的数据量;同样,叶子节点的误差
,N为子树的数据量;同样,叶子节点的误差![]() 。
。
上述公式中,0.5表示修正因子。由于对父节点进行分裂总会得到比父节点分类结果更好的效果,因此,因此从理论上来说,父节点的误差总是不小于孩子节点的误差,因此需要进行修正,给每一个节点都加上0.5的修正因此,在计算误差的时候,子节点由于加上了修正的因子,就无法保证总误差总是低于父节点。
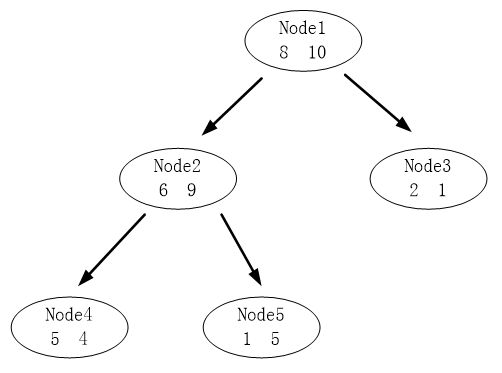
算例:
由于![]() ,所以应该进行剪枝。
,所以应该进行剪枝。
程序设计及源代码(C#版)
程序的设计过程
(1)数据格式
对原始的数据进行数字化处理,并以二维数据的形式存储,每一行表示一条记录,前n-1列表示属性,最后一列表示分类的标签。
如表1的数据可以转化为表2:
表2 初始化后的数据
| 当天天气 |
温度 |
湿度 |
季节 |
明天天气 |
| 1 |
25 |
50 |
1 |
1 |
| 2 |
21 |
48 |
1 |
2 |
| 2 |
18 |
70 |
1 |
3 |
| 1 |
28 |
41 |
2 |
1 |
| 3 |
8 |
65 |
3 |
2 |
| 1 |
18 |
43 |
2 |
1 |
| 2 |
24 |
56 |
4 |
1 |
| 3 |
18 |
76 |
4 |
2 |
| 3 |
31 |
61 |
2 |
1 |
| 2 |
6 |
43 |
3 |
3 |
| 1 |
15 |
55 |
4 |
2 |
| 3 |
4 |
58 |
3 |
3 |
其中,对于“当天天气”属性,数字{1,2,3}分别表示{晴,阴,雨};对于“季节”属性{1,2,3,4}分别表示{春天、夏天、冬天、秋天};对于类标签“明天天气”,数字{1,2,3}分别表示{晴、阴、雨}。
代码如下所示:
static double[][] allData; //存储进行训练的数据
static List<String>[] featureValues; //离散属性对应的离散值
featureValues是链表数组,数组的长度为属性的个数,数组的每个元素为该属性的离散值链表。
(2)两个类:节点类和分裂信息
a)节点类Node
该类表示一个节点,属性包括节点选择的分裂属性、节点的输出类、孩子节点、深度等。注意,与ID3中相比,新增了两个属性:leafWrong和leafNode_Count分别表示叶子节点的总分类误差和叶子节点的个数,主要是为了方便剪枝。
1 class Node 2 { 3 /// <summary> 4 /// 各个子节点对应的取值 5 /// </summary> 6 //public List<String> features; 7 public List<String> features{get;set;} 8 /// <summary> 9 /// 分裂属性的数据类型(1:连续 0:离散) 10 /// </summary> 11 public String feature_Type {get;set;} 12 /// <summary> 13 /// 分裂属性列的下标 14 /// </summary> 15 public String SplitFeature {get;set;} 16 /// <summary> 17 /// 各类别的数量统计 18 /// </summary> 19 public double[] ClassCount {get;set;} 20 /// <summary> 21 /// 数据量 22 /// </summary> 23 public int rowCount { get; set; } 24 /// <summary> 25 /// 各个子节点 26 /// </summary> 27 public List<Node> childNodes {get;set;} 28 /// <summary> 29 /// 父亲节点 30 /// </summary> 31 public Node Parent {get;set;} 32 /// <summary> 33 /// 该节点占比最大的类别 34 /// </summary> 35 public String finalResult {get;set;} 36 /// <summary> 37 /// 数的深度 38 /// </summary> 39 public int deep {get;set;} 40 /// <summary> 41 /// 节点占比最大类的标号 42 /// </summary> 43 public int result {get;set;} 44 /// <summary> 45 /// 子节点的错误数 46 /// </summary> 47 public int leafWrong {get;set;} 48 /// <summary> 49 /// 子节点的数目 50 /// </summary> 51 public int leafNode_Count {get;set;} 52 53 public double getErrorCount() 54 { 55 return rowCount - ClassCount[result]; 56 } 57 #region 58 public void setClassCount(double[] count) 59 { 60 this.ClassCount = count; 61 double max = ClassCount[0]; 62 int result = 0; 63 for (int i = 1; i < ClassCount.Length; i++) 64 { 65 if (max < ClassCount[i]) 66 { 67 max = ClassCount[i]; 68 result = i; 69 } 70 } 71 this.result = result; 72 } 73 #endregion 74 }
b)分裂信息类,该类存储节点进行分裂的信息,包括各个子节点的行坐标、子节点各个类的数目、该节点分裂的属性、属性的类型等。
1 class SplitInfo 2 { 3 /// <summary> 4 /// 分裂的属性下标 5 /// </summary> 6 public int splitIndex { get; set; } 7 /// <summary> 8 /// 数据类型 9 /// </summary> 10 public int type { get; set; } 11 /// <summary> 12 /// 分裂属性的取值 13 /// </summary> 14 public List<String> features { get; set; } 15 /// <summary> 16 /// 各个节点的行坐标链表 17 /// </summary> 18 public List<int>[] temp { get; set; } 19 /// <summary> 20 /// 每个节点各类的数目 21 /// </summary> 22 public double[][] class_Count { get; set; } 23 }
主方法findBestSplit(Node node,List<int> nums,int[] isUsed),该方法对节点进行分裂
其中:
node表示即将进行分裂的节点;
nums表示节点数据的行坐标列表;
isUsed表示到该节点位置所有属性的使用情况;
findBestSplit的这个方法主要有以下几个组成部分:
1)节点分裂停止的判定
节点分裂条件如上文所述,源代码如下:
1 public static bool ifEnd(Node node, double entropy,int[] isUsed) 2 { 3 try 4 { 5 double[] count = node.ClassCount; 6 int rowCount = node.rowCount; 7 int maxResult = 0; 8 #region 数达到某一深度 9 int deep = node.deep; 10 if (deep >= maxDeep) 11 { 12 maxResult = node.result + 1; 13 node.feature_Type=("result"); 14 node.features=(new List<String>() { maxResult + "" }); 15 node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - 1])); 16 node.leafNode_Count = 1; 17 return true; 18 } 19 #endregion 20 #region 纯度(其实跟后面的有点重了,记得要修改) 21 //maxResult = 1; 22 //for (int i = 1; i < count.Length; i++) 23 //{ 24 // if (count[i] / rowCount >= 0.95) 25 // { 26 // node.feature_Type=("result"); 27 // node.features=(new List<String> { "" + (i + 1) }); 28 // node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - 1])); 29 // node.leafNode_Count = 1; 30 // return true; 31 // } 32 //} 33 #endregion 34 #region 熵为0 35 if (entropy == 0) 36 { 37 maxResult = node.result+1; 38 node.feature_Type=("result"); 39 node.features=(new List<String> { maxResult + "" }); 40 node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - 1])); 41 node.leafNode_Count = 1; 42 return true; 43 } 44 #endregion 45 #region 属性已经分完 46 bool flag = true; 47 for (int i = 0; i < isUsed.Length - 1; i++) 48 { 49 if (isUsed[i] == 0) 50 { 51 flag = false; 52 break; 53 } 54 } 55 if (flag) 56 { 57 maxResult = node.result+1; 58 node.feature_Type=("result"); 59 node.features=(new List<String> { "" + (maxResult) }); 60 node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - 1])); 61 node.leafNode_Count = 1; 62 return true; 63 } 64 #endregion 65 #region 数据量少于100 66 if (rowCount < Limit_Node) 67 { 68 maxResult = node.result+1; 69 node.feature_Type=("result"); 70 node.features=(new List<String> { "" + (maxResult) }); 71 node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - 1])); 72 node.leafNode_Count = 1; 73 return true; 74 } 75 #endregion 76 return false; 77 } 78 catch (Exception e) 79 { 80 return false; 81 } 82 }
2)寻找最优的分裂属性
寻找最优的分裂属性需要计算每一个分裂属性分裂后的信息增益率,计算公式上文已给出,其中熵的计算代码如下:
1 public static double CalEntropy(double[] counts, int countAll) 2 { 3 try 4 { 5 double allShang = 0; 6 for (int i = 0; i < counts.Length; i++) 7 { 8 if (counts[i] == 0) 9 { 10 continue; 11 } 12 double rate = counts[i] / countAll; 13 allShang = allShang + rate * Math.Log(rate, 2); 14 } 15 return allShang; 16 } 17 catch (Exception e) 18 { 19 return 0; 20 } 21 }
3)进行分裂,同时对子节点进行迭代处理
其实就是递归的工程,对每一个子节点执行findBestSplit方法进行分裂。
findBestSplit源代码:
1 public static Node findBestSplit(Node node, List<int> nums, int[] isUsed) 2 { 3 try 4 { 5 //判断是否继续分裂 6 double totalShang = CalEntropy(node.ClassCount, node.rowCount); 7 if (ifEnd(node, totalShang,isUsed)) 8 { 9 return node; 10 } 11 #region 变量声明 12 SplitInfo info = new SplitInfo(); 13 int RowCount = nums.Count; //样本总数 14 double jubuMax = 0; //局部最大熵 15 #endregion 16 for (int i = 0; i < isUsed.Length - 1; i++) 17 { 18 if (isUsed[i] == 1) 19 { 20 continue; 21 } 22 #region 离散变量 23 if (type[i] == 0) 24 { 25 int[] allFeatureCount = new int[0]; //所有类别的数量 26 double[][] allCount = new double[allNum[i]][]; 27 for (int j = 0; j < allCount.Length; j++) 28 { 29 allCount[j] = new double[classCount]; 30 } 31 int[] countAllFeature = new int[allNum[i]]; 32 List<int>[] temp = new List<int>[allNum[i]]; 33 for (int j = 0; j < temp.Length; j++) 34 { 35 temp[j] = new List<int>(); 36 } 37 for (int j = 0; j < nums.Count; j++) 38 { 39 int index = Convert.ToInt32(allData[nums[j]][i]); 40 temp[index - 1].Add(nums[j]); 41 countAllFeature[index - 1]++; 42 allCount[index - 1][Convert.ToInt32(allData[nums[j]][lieshu - 1]) - 1]++; 43 } 44 double allShang = 0; 45 double chushu = 0; 46 for (int j = 0; j < allCount.Length; j++) 47 { 48 allShang = allShang + CalEntropy(allCount[j], countAllFeature[j]) * countAllFeature[j] / RowCount; 49 if (countAllFeature[j] > 0) 50 { 51 double rate = countAllFeature[j] / Convert.ToDouble(RowCount); 52 chushu = chushu + rate * Math.Log(rate, 2); 53 } 54 } 55 allShang = (-totalShang + allShang); 56 if (allShang > jubuMax) 57 { 58 info.features = new List<string>(); 59 info.type = 0; 60 info.temp = temp; 61 info.splitIndex = i; 62 info.class_Count = allCount; 63 jubuMax = allShang; 64 allFeatureCount = countAllFeature; 65 } 66 } 67 #endregion 68 #region 连续变量 69 else 70 { 71 double[] leftCount = new double[classCount]; //做节点各个类别的数量 72 double[] rightCount = new double[classCount]; //右节点各个类别的数量 73 double[] count1 = new double[classCount]; //子集1的统计量 74 //double[] count2 = new double[node.getCount().Length]; //子集2的统计量 75 double[] count2 = new double[node.ClassCount.Length]; //子集2的统计量 76 for (int j = 0; j < node.ClassCount.Length; j++) 77 { 78 count2[j] = node.ClassCount[j]; 79 } 80 int all1 = 0; //子集1的样本量 81 int all2 = nums.Count; //子集2的样本量 82 double lastValue = 0; //上一个记录的类别 83 double currentValue = 0; //当前类别 84 double lastPoint = 0; //上一个点的值 85 double currentPoint = 0; //当前点的值 86 int splitPoint = 0; 87 double splitValue = 0; 88 double[] values = new double[nums.Count]; 89 for (int j = 0; j < values.Length; j++) 90 { 91 values[j] = allData[nums[j]][i]; 92 } 93 QSort(values, nums, 0, nums.Count - 1); 94 double chushu = 0; 95 double lianxuMax = 0; //连续型属性的最大熵 96 for (int j = 0; j < nums.Count - 1; j++) 97 { 98 currentValue = allData[nums[j]][lieshu - 1]; 99 currentPoint = allData[nums[j]][i]; 100 if (j == 0) 101 { 102 lastValue = currentValue; 103 lastPoint = currentPoint; 104 } 105 if (currentValue != lastValue) 106 { 107 double shang1 = CalEntropy(count1, all1); 108 double shang2 = CalEntropy(count2, all2); 109 double allShang = shang1 * all1 / (all1 + all2) + shang2 * all2 / (all1 + all2); 110 allShang = (-totalShang + allShang); 111 if (lianxuMax < allShang) 112 { 113 lianxuMax = allShang; 114 for (int k = 0; k < count1.Length; k++) 115 { 116 leftCount[k] = count1[k]; 117 rightCount[k] = count2[k]; 118 } 119 splitPoint = j; 120 splitValue = (currentPoint + lastPoint) / 2; 121 } 122 } 123 all1++; 124 count1[Convert.ToInt32(currentValue) - 1]++; 125 count2[Convert.ToInt32(currentValue) - 1]--; 126 all2--; 127 lastValue = currentValue; 128 lastPoint = currentPoint; 129 } 130 double rate1 = Convert.ToDouble(leftCount[0] + leftCount[1]) / (leftCount[0] + leftCount[1] + rightCount[0] + rightCount[1]); 131 chushu = 0; 132 if (rate1 > 0) 133 { 134 chushu = chushu + rate1 * Math.Log(rate1, 2); 135 } 136 double rate2 = Convert.ToDouble(rightCount[0] + rightCount[1]) / (leftCount[0] + leftCount[1] + rightCount[0] + rightCount[1]); 137 if (rate2 > 0) 138 { 139 chushu = chushu + rate2 * Math.Log(rate2, 2); 140 } 141 //lianxuMax = lianxuMax ; 142 //lianxuMax = lianxuMax; 143 if (lianxuMax > jubuMax) 144 { 145 //info.setSplitIndex(i); 146 info.splitIndex=(i); 147 //info.setFeatures(new List<String> { splitValue + "" }); 148 info.features = (new List<String> { splitValue + "" }); 149 //info.setType(1); 150 info.type=(1); 151 jubuMax = lianxuMax; 152 //info.setType(1); 153 List<int>[] allInt = new List<int>[2]; 154 allInt[0] = new List<int>(); 155 allInt[1] = new List<int>(); 156 for (int k = 0; k < splitPoint; k++) 157 { 158 allInt[0].Add(nums[k]); 159 } 160 for (int k = splitPoint; k < nums.Count; k++) 161 { 162 allInt[1].Add(nums[k]); 163 } 164 info.temp=(allInt); 165 //info.setTemp(allInt); 166 double[][] alls = new double[2][]; 167 alls[0] = new double[leftCount.Length]; 168 alls[1] = new double[leftCount.Length]; 169 for (int k = 0; k < leftCount.Length; k++) 170 { 171 alls[0][k] = leftCount[k]; 172 alls[1][k] = rightCount[k]; 173 } 174 info.class_Count=(alls); 175 //info.setclassCount(alls); 176 } 177 } 178 #endregion 179 } 180 #region 如果找不到最佳的分裂属性,则设为叶节点 181 if (info.splitIndex == -1) 182 { 183 double[] finalCount = node.ClassCount; 184 double max = finalCount[0]; 185 int result = 1; 186 for (int i = 1; i < finalCount.Length; i++) 187 { 188 if (finalCount[i] > max) 189 { 190 max = finalCount[i]; 191 result = (i + 1); 192 } 193 } 194 node.feature_Type=("result"); 195 node.features=(new List<String> { "" + result }); 196 return node; 197 } 198 #endregion 199 #region 分裂 200 int deep = node.deep; 201 node.SplitFeature=("" + info.splitIndex); 202 203 List<Node> childNode = new List<Node>(); 204 int[] used = new int[isUsed.Length]; 205 for (int i = 0; i < used.Length; i++) 206 { 207 used[i] = isUsed[i]; 208 } 209 if (info.type == 0) 210 { 211 used[info.splitIndex] = 1; 212 node.feature_Type=("离散"); 213 } 214 else 215 { 216 used[info.splitIndex] = 0; 217 node.feature_Type=("连续"); 218 } 219 int sumLeaf = 0; 220 int sumWrong = 0; 221 List<int>[] rowIndex = info.temp; 222 List<String> features = info.features; 223 for (int j = 0; j < rowIndex.Length; j++) 224 { 225 if (rowIndex[j].Count == 0) 226 { 227 continue; 228 } 229 if (info.type == 0) 230 features.Add("" + (j + 1)); 231 Node node1 = new Node(); 232 node1.setClassCount(info.class_Count[j]); 233 node1.deep=(deep + 1); 234 node1.rowCount = info.temp[j].Count; 235 node1 = findBestSplit(node1, info.temp[j], used); 236 sumLeaf += node1.leafNode_Count; 237 sumWrong += node1.leafWrong; 238 childNode.Add(node1); 239 } 240 node.leafNode_Count = (sumLeaf); 241 node.leafWrong = (sumWrong); 242 node.features=(features); 243 node.childNodes=(childNode); 244 #endregion 245 return node; 246 } 247 catch (Exception e) 248 { 249 Console.WriteLine(e.StackTrace); 250 return node; 251 } 252 }
(4)剪枝
悲观剪枝方法(PEP):
1 public static void prune(Node node) 2 { 3 if (node.feature_Type == "result") 4 return; 5 double treeWrong = node.getErrorCount() + 0.5; 6 double leafError = node.leafWrong + 0.5 * node.leafNode_Count; 7 double var = Math.Sqrt(leafError * (1 - Convert.ToDouble(leafError) / node.nums.Count)); 8 double panbie = leafError + var - treeWrong; 9 if (panbie > 0) 10 { 11 node.feature_Type=("result"); 12 node.childNodes=(null); 13 int result = (node.result + 1); 14 node.features=(new List<String>() { "" + result }); 15 } 16 else 17 { 18 List<Node> childNodes = node.childNodes; 19 for (int i = 0; i < childNodes.Count; i++) 20 { 21 prune(childNodes[i]); 22 } 23 } 24 }
C4.5核心算法的所有源代码:
1 #region C4.5核心算法 2 /// <summary> 3 /// 测试 4 /// </summary> 5 /// <param name="node"></param> 6 /// <param name="data"></param> 7 public static String findResult(Node node, String[] data) 8 { 9 List<String> featrues = node.features; 10 String type = node.feature_Type; 11 if (type == "result") 12 { 13 return featrues[0]; 14 } 15 int split = Convert.ToInt32(node.SplitFeature); 16 List<Node> childNodes = node.childNodes; 17 double[] resultCount = node.ClassCount; 18 if (type == "连续") 19 { 20 double value = Convert.ToDouble(featrues[0]); 21 if (Convert.ToDouble(data[split]) <= value) 22 { 23 return findResult(childNodes[0], data); 24 } 25 else 26 { 27 return findResult(childNodes[1], data); 28 } 29 } 30 else 31 { 32 for (int i = 0; i < featrues.Count; i++) 33 { 34 if (data[split] == featrues[i]) 35 { 36 return findResult(childNodes[i], data); 37 } 38 if (i == featrues.Count - 1) 39 { 40 double count = resultCount[0]; 41 int maxInt = 0; 42 for (int j = 1; j < resultCount.Length; j++) 43 { 44 if (count < resultCount[j]) 45 { 46 count = resultCount[j]; 47 maxInt = j; 48 } 49 } 50 return findResult(childNodes[0], data); 51 } 52 } 53 } 54 return null; 55 } 56 /// <summary> 57 /// 判断是否还需要分裂 58 /// </summary> 59 /// <param name="node"></param> 60 /// <returns></returns> 61 public static bool ifEnd(Node node, double entropy,int[] isUsed) 62 { 63 try 64 { 65 double[] count = node.ClassCount; 66 int rowCount = node.rowCount; 67 int maxResult = 0; 68 #region 数达到某一深度 69 int deep = node.deep; 70 if (deep >= maxDeep) 71 { 72 maxResult = node.result + 1; 73 node.feature_Type=("result"); 74 node.features=(new List<String>() { maxResult + "" }); 75 node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - 1])); 76 node.leafNode_Count = 1; 77 return true; 78 } 79 #endregion 80 #region 纯度(其实跟后面的有点重了,记得要修改) 81 //maxResult = 1; 82 //for (int i = 1; i < count.Length; i++) 83 //{ 84 // if (count[i] / rowCount >= 0.95) 85 // { 86 // node.feature_Type=("result"); 87 // node.features=(new List<String> { "" + (i + 1) }); 88 // node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - 1])); 89 // node.leafNode_Count = 1; 90 // return true; 91 // } 92 //} 93 #endregion 94 #region 熵为0 95 if (entropy == 0) 96 { 97 maxResult = node.result+1; 98 node.feature_Type=("result"); 99 node.features=(new List<String> { maxResult + "" }); 100 node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - 1])); 101 node.leafNode_Count = 1; 102 return true; 103 } 104 #endregion 105 #region 属性已经分完 106 bool flag = true; 107 for (int i = 0; i < isUsed.Length - 1; i++) 108 { 109 if (isUsed[i] == 0) 110 { 111 flag = false; 112 break; 113 } 114 } 115 if (flag) 116 { 117 maxResult = node.result+1; 118 node.feature_Type=("result"); 119 node.features=(new List<String> { "" + (maxResult) }); 120 node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - 1])); 121 node.leafNode_Count = 1; 122 return true; 123 } 124 #endregion 125 #region 数据量少于100 126 if (rowCount < Limit_Node) 127 { 128 maxResult = node.result+1; 129 node.feature_Type=("result"); 130 node.features=(new List<String> { "" + (maxResult) }); 131 node.leafWrong=(rowCount - Convert.ToInt32(count[maxResult - 1])); 132 node.leafNode_Count = 1; 133 return true; 134 } 135 #endregion 136 return false; 137 } 138 catch (Exception e) 139 { 140 return false; 141 } 142 } 143 #region 排序算法 144 public static void InsertSort(double[] values, List<int> arr, int StartIndex, int endIndex) 145 { 146 for (int i = StartIndex + 1; i <= endIndex; i++) 147 { 148 int key = arr[i]; 149 double init = values[i]; 150 int j = i - 1; 151 while (j >= StartIndex && values[j] > init) 152 { 153 arr[j + 1] = arr[j]; 154 values[j + 1] = values[j]; 155 j--; 156 } 157 arr[j + 1] = key; 158 values[j + 1] = init; 159 } 160 } 161 static int SelectPivotMedianOfThree(double[] values, List<int> arr, int low, int high) 162 { 163 int mid = low + ((high - low) >> 1);//计算数组中间的元素的下标 164 165 //使用三数取中法选择枢轴 166 if (values[mid] > values[high])//目标: arr[mid] <= arr[high] 167 { 168 swap(values, arr, mid, high); 169 } 170 if (values[low] > values[high])//目标: arr[low] <= arr[high] 171 { 172 swap(values, arr, low, high); 173 } 174 if (values[mid] > values[low]) //目标: arr[low] >= arr[mid] 175 { 176 swap(values, arr, mid, low); 177 } 178 //此时,arr[mid] <= arr[low] <= arr[high] 179 return low; 180 //low的位置上保存这三个位置中间的值 181 //分割时可以直接使用low位置的元素作为枢轴,而不用改变分割函数了 182 } 183 static void swap(double[] values, List<int> arr, int t1, int t2) 184 { 185 double temp = values[t1]; 186 values[t1] = values[t2]; 187 values[t2] = temp; 188 int key = arr[t1]; 189 arr[t1] = arr[t2]; 190 arr[t2] = key; 191 } 192 static void QSort(double[] values, List<int> arr, int low, int high) 193 { 194 int first = low; 195 int last = high; 196 197 int left = low; 198 int right = high; 199 200 int leftLen = 0; 201 int rightLen = 0; 202 203 if (high - low + 1 < 10) 204 { 205 InsertSort(values, arr, low, high); 206 return; 207 } 208 209 //一次分割 210 int key = SelectPivotMedianOfThree(values, arr, low, high);//使用三数取中法选择枢轴 211 double inti = values[key]; 212 int currentKey = arr[key]; 213 214 while (low < high) 215 { 216 while (high > low && values[high] >= inti) 217 { 218 if (values[high] == inti)//处理相等元素 219 { 220 swap(values, arr, right, high); 221 right--; 222 rightLen++; 223 } 224 high--; 225 } 226 arr[low] = arr[high]; 227 values[low] = values[high]; 228 while (high > low && values[low] <= inti) 229 { 230 if (values[low] == inti) 231 { 232 swap(values, arr, left, low); 233 left++; 234 leftLen++; 235 } 236 low++; 237 } 238 arr[high] = arr[low]; 239 values[high] = values[low]; 240 } 241 arr[low] = currentKey; 242 values[low] = values[key]; 243 //一次快排结束 244 //把与枢轴key相同的元素移到枢轴最终位置周围 245 int i = low - 1; 246 int j = first; 247 while (j < left && values[i] != inti) 248 { 249 swap(values, arr, i, j); 250 i--; 251 j++; 252 } 253 i = low + 1; 254 j = last; 255 while (j > right && values[i] != inti) 256 { 257 swap(values, arr, i, j); 258 i++; 259 j--; 260 } 261 QSort(values, arr, first, low - 1 - leftLen); 262 QSort(values, arr, low + 1 + rightLen, last); 263 } 264 #endregion 265 /// <summary> 266 /// 寻找最佳的分裂点 267 /// </summary> 268 /// <param name="num"></param> 269 /// <param name="node"></param> 270 public static Node findBestSplit(Node node, List<int> nums, int[] isUsed) 271 { 272 try 273 { 274 //判断是否继续分裂 275 double totalShang = CalEntropy(node.ClassCount, node.rowCount); 276 if (ifEnd(node, totalShang,isUsed)) 277 { 278 return node; 279 } 280 #region 变量声明 281 SplitInfo info = new SplitInfo(); 282 int RowCount = nums.Count; //样本总数 283 double jubuMax = 0; //局部最大熵 284 #endregion 285 for (int i = 0; i < isUsed.Length - 1; i++) 286 { 287 if (isUsed[i] == 1) 288 { 289 continue; 290 } 291 #region 离散变量 292 if (type[i] == 0) 293 { 294 int[] allFeatureCount = new int[0]; //所有类别的数量 295 double[][] allCount = new double[allNum[i]][]; 296 for (int j = 0; j < allCount.Length; j++) 297 { 298 allCount[j] = new double[classCount]; 299 } 300 int[] countAllFeature = new int[allNum[i]]; 301 List<int>[] temp = new List<int>[allNum[i]]; 302 for (int j = 0; j < temp.Length; j++) 303 { 304 temp[j] = new List<int>(); 305 } 306 for (int j = 0; j < nums.Count; j++) 307 { 308 int index = Convert.ToInt32(allData[nums[j]][i]); 309 temp[index - 1].Add(nums[j]); 310 countAllFeature[index - 1]++; 311 allCount[index - 1][Convert.ToInt32(allData[nums[j]][lieshu - 1]) - 1]++; 312 } 313 double allShang = 0; 314 double chushu = 0; 315 for (int j = 0; j < allCount.Length; j++) 316 { 317 allShang = allShang + CalEntropy(allCount[j], countAllFeature[j]) * countAllFeature[j] / RowCount; 318 if (countAllFeature[j] > 0) 319 { 320 double rate = countAllFeature[j] / Convert.ToDouble(RowCount); 321 chushu = chushu + rate * Math.Log(rate, 2); 322 } 323 } 324 allShang = (-totalShang + allShang); 325 if (allShang > jubuMax) 326 { 327 info.features = new List<string>(); 328 info.type = 0; 329 info.temp = temp; 330 info.splitIndex = i; 331 info.class_Count = allCount; 332 jubuMax = allShang; 333 allFeatureCount = countAllFeature; 334 } 335 } 336 #endregion 337 #region 连续变量 338 else 339 { 340 double[] leftCount = new double[classCount]; //做节点各个类别的数量 341 double[] rightCount = new double[classCount]; //右节点各个类别的数量 342 double[] count1 = new double[classCount]; //子集1的统计量 343 //double[] count2 = new double[node.getCount().Length]; //子集2的统计量 344 double[] count2 = new double[node.ClassCount.Length]; //子集2的统计量 345 for (int j = 0; j < node.ClassCount.Length; j++) 346 { 347 count2[j] = node.ClassCount[j]; 348 } 349 int all1 = 0; //子集1的样本量 350 int all2 = nums.Count; //子集2的样本量 351 double lastValue = 0; //上一个记录的类别 352 double currentValue = 0; //当前类别 353 double lastPoint = 0; //上一个点的值 354 double currentPoint = 0; //当前点的值 355 int splitPoint = 0; 356 double splitValue = 0; 357 double[] values = new double[nums.Count]; 358 for (int j = 0; j < values.Length; j++) 359 { 360 values[j] = allData[nums[j]][i]; 361 } 362 QSort(values, nums, 0, nums.Count - 1); 363 double chushu = 0; 364 double lianxuMax = 0; //连续型属性的最大熵 365 for (int j = 0; j < nums.Count - 1; j++) 366 { 367 currentValue = allData[nums[j]][lieshu - 1]; 368 currentPoint = allData[nums[j]][i]; 369 if (j == 0) 370 { 371 lastValue = currentValue; 372 lastPoint = currentPoint; 373 } 374 if (currentValue != lastValue) 375 { 376 double shang1 = CalEntropy(count1, all1); 377 double shang2 = CalEntropy(count2, all2); 378 double allShang = shang1 * all1 / (all1 + all2) + shang2 * all2 / (all1 + all2); 379 allShang = (-totalShang + allShang); 380 if (lianxuMax < allShang) 381 { 382 lianxuMax = allShang; 383 for (int k = 0; k < count1.Length; k++) 384 { 385 leftCount[k] = count1[k]; 386 rightCount[k] = count2[k]; 387 } 388 splitPoint = j; 389 splitValue = (currentPoint + lastPoint) / 2; 390 } 391 } 392 all1++; 393 count1[Convert.ToInt32(currentValue) - 1]++; 394 count2[Convert.ToInt32(currentValue) - 1]--; 395 all2--; 396 lastValue = currentValue; 397 lastPoint = currentPoint; 398 } 399 double rate1 = Convert.ToDouble(leftCount[0] + leftCount[1]) / (leftCount[0] + leftCount[1] + rightCount[0] + rightCount[1]); 400 chushu = 0; 401 if (rate1 > 0) 402 { 403 chushu = chushu + rate1 * Math.Log(rate1, 2); 404 } 405 double rate2 = Convert.ToDouble(rightCount[0] + rightCount[1]) / (leftCount[0] + leftCount[1] + rightCount[0] + rightCount[1]); 406 if (rate2 > 0) 407 { 408 chushu = chushu + rate2 * Math.Log(rate2, 2); 409 } 410 //lianxuMax = lianxuMax ; 411 //lianxuMax = lianxuMax; 412 if (lianxuMax > jubuMax) 413 { 414 //info.setSplitIndex(i); 415 info.splitIndex=(i); 416 //info.setFeatures(new List<String> { splitValue + "" }); 417 info.features = (new List<String> { splitValue + "" }); 418 //info.setType(1); 419 info.type=(1); 420 jubuMax = lianxuMax; 421 //info.setType(1); 422 List<int>[] allInt = new List<int>[2]; 423 allInt[0] = new List<int>(); 424 allInt[1] = new List<int>(); 425 for (int k = 0; k < splitPoint; k++) 426 { 427 allInt[0].Add(nums[k]); 428 } 429 for (int k = splitPoint; k < nums.Count; k++) 430 { 431 allInt[1].Add(nums[k]); 432 } 433 info.temp=(allInt); 434 //info.setTemp(allInt); 435 double[][] alls = new double[2][]; 436 alls[0] = new double[leftCount.Length]; 437 alls[1] = new double[leftCount.Length]; 438 for (int k = 0; k < leftCount.Length; k++) 439 { 440 alls[0][k] = leftCount[k]; 441 alls[1][k] = rightCount[k]; 442 } 443 info.class_Count=(alls); 444 //info.setclassCount(alls); 445 } 446 } 447 #endregion 448 } 449 #region 如果找不到最佳的分裂属性,则设为叶节点 450 if (info.splitIndex == -1) 451 { 452 double[] finalCount = node.ClassCount; 453 double max = finalCount[0]; 454 int result = 1; 455 for (int i = 1; i < finalCount.Length; i++) 456 { 457 if (finalCount[i] > max) 458 { 459 max = finalCount[i]; 460 result = (i + 1); 461 } 462 } 463 node.feature_Type=("result"); 464 node.features=(new List<String> { "" + result }); 465 return node; 466 } 467 #endregion 468 #region 分裂 469 int deep = node.deep; 470 node.SplitFeature=("" + info.splitIndex); 471 472 List<Node> childNode = new List<Node>(); 473 int[] used = new int[isUsed.Length]; 474 for (int i = 0; i < used.Length; i++) 475 { 476 used[i] = isUsed[i]; 477 } 478 if (info.type == 0) 479 { 480 used[info.splitIndex] = 1; 481 node.feature_Type=("离散"); 482 } 483 else 484 { 485 used[info.splitIndex] = 0; 486 node.feature_Type=("连续"); 487 } 488 int sumLeaf = 0; 489 int sumWrong = 0; 490 List<int>[] rowIndex = info.temp; 491 List<String> features = info.features; 492 for (int j = 0; j < rowIndex.Length; j++) 493 { 494 if (rowIndex[j].Count == 0) 495 { 496 continue; 497 } 498 if (info.type == 0) 499 features.Add("" + (j + 1)); 500 Node node1 = new Node(); 501 node1.setClassCount(info.class_Count[j]); 502 node1.deep=(deep + 1); 503 node1.rowCount = info.temp[j].Count; 504 node1 = findBestSplit(node1, info.temp[j], used); 505 sumLeaf += node1.leafNode_Count; 506 sumWrong += node1.leafWrong; 507 childNode.Add(node1); 508 } 509 node.leafNode_Count = (sumLeaf); 510 node.leafWrong = (sumWrong); 511 node.features=(features); 512 node.childNodes=(childNode); 513 #endregion 514 return node; 515 } 516 catch (Exception e) 517 { 518 Console.WriteLine(e.StackTrace); 519 return node; 520 } 521 } 522 /// <summary> 523 /// 计算熵 524 /// </summary> 525 /// <param name="counts"></param> 526 /// <param name="countAll"></param> 527 /// <returns></returns> 528 public static double CalEntropy(double[] counts, int countAll) 529 { 530 try 531 { 532 double allShang = 0; 533 for (int i = 0; i < counts.Length; i++) 534 { 535 if (counts[i] == 0) 536 { 537 continue; 538 } 539 double rate = counts[i] / countAll; 540 allShang = allShang + rate * Math.Log(rate, 2); 541 } 542 return allShang; 543 } 544 catch (Exception e) 545 { 546 return 0; 547 } 548 } 549 550 #region 悲观剪枝 551 public static void prune(Node node) 552 { 553 if (node.feature_Type == "result") 554 return; 555 double treeWrong = node.getErrorCount() + 0.5; 556 double leafError = node.leafWrong + 0.5 * node.leafNode_Count; 557 double var = Math.Sqrt(leafError * (1 - Convert.ToDouble(leafError) / node.rowCount)); 558 double panbie = leafError + var - treeWrong; 559 if (panbie > 0) 560 { 561 node.feature_Type = "result"; 562 node.childNodes = null; 563 int result = node.result + 1; 564 node.features= new List<String>() { "" + result }; 565 } 566 else 567 { 568 List<Node> childNodes = node.childNodes; 569 for (int i = 0; i < childNodes.Count; i++) 570 { 571 prune(childNodes[i]); 572 } 573 } 574 } 575 #endregion 576 #endregion
总结:
要记住,C4.5是分类树最终要的算法,算法的思想其实很简单,但是分类的准确性高。可以说C4.5是ID3的升级版和强化版,解决了ID3未能解决的问题。要重点记住以下几个方面:
1.C4.5是采用信息增益率选择分裂的属性,解决了ID3选择属性时的偏向性问题;
2.C4.5能够对连续数据进行处理,采用一刀切的方式将连续型的数据切成两份,在选择切割点的时候使用信息增益作为择优的条件;
3.C4.5采用悲观剪枝的策略,一定程度上降低了过拟合的影响。