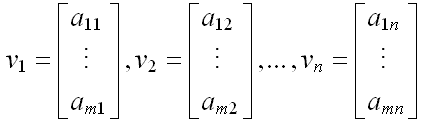原文:http://www.cnblogs.com/JCSU/articles/1490363.html
一、用矩阵运算法解线性方程组
1、矩阵运算规则及MATLAB实例
(1) 矩阵加(减)法:即两矩阵对应元素相加减,要求两矩阵的阶数必须相同。
C = A + B
(2) 矩阵乘法:m×p阶矩阵A与p×n阶矩阵B的乘积C是一个m×n阶的矩阵。元素C(i, j)的值为A矩阵的第i行和B矩阵的第j列对应元素乘积的和。
A*B = C
矩阵乘法一般不满足交换律,即:A*B ≠ B*A
例:
A =
1 2 3
>> B=[4; 5; 6]
B =
4
5
6
>> A*B %结果是一个标量
ans =
32
>> B*A %结果是一个矩阵
ans =
4 8 12
5 10 15
6 12 18
>>
(3) 矩阵求逆:矩阵的逆阵V定义为满足V*A = I (I为与A同阶的单位矩阵)。只有方阵才可以求逆,而且此方阵的行列式必须不为零,det(A) ≠ 0。如果det(A) = 0,求逆时就会出现无穷大,此时的矩阵称为奇异的。
例:
A =
4 8 12
5 10 15
6 12 18
>> B
B =
4 8 12
6 10 15
7 12 4
>> det(A) %矩阵A的行列式为零
ans =
0
>> det(B) %矩阵B的行列式不为零
ans =
112
>> inv(A) %对矩阵A求逆时出现无穷大(Inf)
Warning: Matrix is singular to working precision.
ans =
Inf Inf Inf
Inf Inf Inf
Inf Inf Inf
>> inv(B) %对矩阵B求逆正常
ans =
-1.2500 1.0000 0
0.7232 -0.6071 0.1071
0.0179 0.0714 -0.0714
>>
(4) 矩阵转置:矩阵的行列互换后构成转置矩阵。如果A是m×n阶的,则AT是n×m阶的。
例:
A =
4 8 12
5 10 15
>> B=A'
B =
4 5
8 10
12 15
(5) 矩阵分块:矩阵A可以划分成许多小矩阵。
例:
A =
3 -4 3 2 -1
0 -6 0 -3 -3
4 -3 4 2 -2
1 1 1 0 -1
>> A1=A(1:3, 1:3)
A1 =
3 -4 3
0 -6 0
4 -3 4
>> A2=A(1:3, 4:5)
A2 =
2 -1
-3 -3
2 -2
>> A3=A(4, 1:4)
A3 =
1 1 1 0
>> A4=A(4, 5)
A4 =
-1
>>
(5) 矩阵分解为向量:把矩阵沿行向或列向分解为单列或单行向量,常见的是分解为列向量。
其中:
(6) 行向量左乘列向量:要求两向量的长度必须一致,结果为一个标量。得出的是向量各分量的平方和。如果这些分量是正交的,则得出的是向量的长度平方。它的平方根就是向量长度,也称为向量的范数或2范数。
行向量左乘列向量得到的是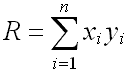 ,在工程中具有这样计算形式的问题很多,比如用它计算两个向量x和y之间的相关性。
,在工程中具有这样计算形式的问题很多,比如用它计算两个向量x和y之间的相关性。
(7) 列向量左乘行向量:如果列向量的长度为n,行向量的长度为m,则相乘会得出一个n×m的矩阵,这种方法常常用来生成和计算一些复杂的大矩阵。
(8) 矩阵乘法和幂次:A^2 = A*A, A^n = A*A*...*A。根据矩阵相乘内阶数必须相等,只有方阵才能乘方和幂次。
2、初等变换乘子矩阵的生成及MATLAB实例
本节通过将原矩阵左乘变换的单位矩阵实现矩阵的初等行变换:
(1) 行交换:将矩阵A的第 i , j 两行互换位置。
% 行交换:交换矩阵A的第1行和第3行
% 步骤1:得到一个5阶单位阵:E=eye(5)
% 步骤2:交换E的第1行和第3行得到矩阵 E1
% 步骤3:矩阵A左乘矩阵E1得到交换后 的矩阵
>> A
A =
3 -4 3 2 -1
0 -6 0 -3 -3
4 -3 4 2 -2
1 1 1 0 -1
-2 6 -2 1 3
>>
E1 =
0 0 1 0 0
0 1 0 0 0
1 0 0 0 0
0 0 0 1 0
0 0 0 0 1
>> E1*A
ans =
4 -3 4 2 -2
0 -6 0 -3 -3
3 -4 3 2 -1
1 1 1 0 -1
-2 6 -2 1 3
>>
写成函数E1gen(A,i,j):
n=size(A); %求矩阵A的行数和列数
m=min(n); %获取矩阵行数和列数中的最小值
E=eye(m); %产生单位对角阵
E(i,i)=0; E(j,j)=0; E(i,j)=1; E(j,i)=1;
(2) 行乘数:将矩阵A的第 i 行乘以 k 。
% 行乘数:将矩阵A的第4行乘以5
% 步骤1:得到一个5阶单位阵:E=eye(5)
% 步骤2:将单位阵E中的元素E(4,4)乘以5得到矩阵E2
% 步骤3:矩阵A左乘矩阵E2得到变换后 的矩阵
>> A
A =
3 -4 3 2 -1
0 -6 0 -3 -3
4 -3 4 2 -2
1 1 1 0 -1
-2 6 -2 1 3
>> E2
E2 =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 5 0
0 0 0 0 1
>> E2*A
ans =
3 -4 3 2 -1
0 -6 0 -3 -3
4 -3 4 2 -2
5 5 5 0 -5
-2 6 -2 1 3
>>
写成函数E2gen(A,i,k):
n=size(A);
m=min(n);%获取矩阵行数和列数中的最小值
E=eye(m);%产生单位对角阵
E(i,i)=k;
(3) 行相加:将矩阵的第 i 行乘以 k,加到第 j 行。
% 行乘数加到另一行:将矩阵A的第4行乘以2加到第5行
% 步骤1:得到一个5阶单位阵:E=eye(5)
% 步骤2:将单位阵E中的元素E(5,4)乘以2得到矩阵E3
% 步骤3:矩阵A左乘矩阵E3得到变换后的矩阵
>> A
A =
3 -4 3 2 -1
0 -6 0 -3 -3
4 -3 4 2 -2
1 1 1 0 -1
-2 6 -2 1 3
>> E3
E3 =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 2 1
>> E3*A
ans =
3 -4 3 2 -1
0 -6 0 -3 -3
4 -3 4 2 -2
1 1 1 0 -1
0 8 0 1 1
>>
写成函数E3gen(A,i,j,k):
n=size(A);
m=min(n);%获取矩阵行数和列数中的最小值
E=eye(m);%产生单位对角阵
E(j,i)=k;
实例:
要消去下列矩阵的A(2,1),求乘子矩阵E3
3 -4 3 2 -1
6 -6 0 -3 -3
4 -3 4 2 -2
1 1 1 0 -1
-2 6 -2 1 3
在第二行加以第一行乘 -A(2,1)/A(1,1) = -2,故令E3 = E3gen(A,1,2,-2)
E3 =
1 0 0 0 0
-2 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
>> E3*A
ans =
3 -4 3 2 -1
0 2 -6 -7 -1
4 -3 4 2 -2
1 1 1 0 -1
-2 6 -2 1 3
>>
综上可知:
1、 行阶梯生成等价于矩阵左乘
因此,整个行阶梯形式U的生成过程,可以看作把原矩阵左乘以一系列的初等变换矩阵E1和E3。把这些初等矩阵的连乘积写成EX,则有: U=EX*A,设其逆为L:
从而有 L*U=A
就是说,A可以分解为一个准下三角矩阵L和一个上三角(即行阶梯)矩阵U的乘积。MATLAB提供了三角分解的函数lu,它的调用方法是:[L,U]=lu(A)
2、 lu分解是求行阶梯的一个方法
用lu函数求出的U实际上就是A的行阶梯形式(不是简化行阶梯形式)。所以,求简化行阶梯形式用rref函数,而求行阶梯形式可以用lu 函数。不过,它和我们用消元运算所得U的数据不一定相同,尽管得出的阶次和阶梯形状相同。但因为行阶梯形式可以有无数种,用不同步骤算出的结果也不同。只有变成简化行阶梯形式,才能进行比较,看它是不是惟一的。
3、行列式
(1) 行列式的几何意义:
行列式的几何意义是面积或体积,它的用途很单一,就是判断奇异性,连正负号都不必关心。
(2) 行列式的计算方法:
计算行列式的最好方法还是行阶梯法,可以利用lu分解
[L,U] = lu(A)
把A分解为一个准下三角矩阵L和一个上三角矩阵U的乘积。因为det(L) = 1,所以U和A的行列式相等。
det(A) = det(U)
而三角矩阵U的det(U)很好求。只要把U的主对角线元素连乘就可得到它的行列式。
实例:
A =
10 8 6 4 1
2 5 8 9 4
6 0 9 9 8
5 8 7 4 0
9 4 2 9 1
>> [L U]=lu(A)
L =
1.0000 0 0 0 0
0.2000 -0.7083 1.0000 0 0
0.6000 1.0000 0 0 0
0.5000 -0.8333 0.8000 -0.2953 1.0000
0.9000 0.6667 -0.6588 1.0000 0
U =
10.0000 8.0000 6.0000 4.0000 1.0000
0 -4.8000 5.4000 6.6000 7.4000
0 0 10.6250 12.8750 9.0417
0 0 0 9.4824 1.1235
0 0 0 0 -1.2349
>> du=diag(U)
du =
10.0000
-4.8000
10.6250
9.4824
-1.2349
>> result=prod(du)
result =
5.9720e+003
>>
用det求A的行列式值得到相同的结果:
ans =
5972
>>
4、矩阵的秩和矩阵求逆
矩阵的秩:
(1) 按定义,矩阵的秩是矩阵A中行列式不等于零的最高阶子式的阶次。是用以衡量联立方程中有效方程数目的指数。
(2) 按照定义来计算矩阵的秩,可能遇到的问题也是子矩阵的数量很大,每个矩阵的行列式计算又非常麻烦,其计算量也将是不可接受的天文数字。
(3) 计算矩阵的秩的最好方法是行阶梯法,行阶梯化简后非全为零的行数就是该矩阵的秩。用MATLAB函数r=rank(A)可以检验A的秩,rank函数对A是否是方阵没有要求,即可以有m≠n。
矩阵求逆:
(1) 对于n×n方阵A,当r=n时,称A是满秩的,若r<n,必有det(A) = 0,称A是欠秩的或奇异的。奇异矩阵不可以求逆。
(2) 矩阵求逆的最简单方法也是行阶梯化简,其方法是设定一个由A和I组成的增广矩阵C = [A,I],求C的简化行阶梯形式UC = rref([A,I]),得出UC = [I,V]。V就显示出这个逆矩阵的内容。
求逆实例:
A =
3 0 3 -6
5 -1 1 -5
-3 1 4 -9
1 -3 4 -4
>> C=[A,eye(4)]
C =
3 0 3 -6 1 0 0 0
5 -1 1 -5 0 1 0 0
-3 1 4 -9 0 0 1 0
1 -3 4 -4 0 0 0 1
>> UC=rref(C) %UC右边四列就是矩阵A的逆
UC =
1.0000 0 0 0 0.2323 -0.0101 -0.1313 -0.0404
0 1.0000 0 0 0.5354 -0.3131 -0.0707 -0.2525
0 0 1.0000 0 0.5859 -0.4747 -0.1717 0.1010
0 0 0 1.0000 0.2424 -0.2424 -0.1515 0.0303
>> V=UC(:,5:8)
V =
0.2323 -0.0101 -0.1313 -0.0404
0.5354 -0.3131 -0.0707 -0.2525
0.5859 -0.4747 -0.1717 0.1010
0.2424 -0.2424 -0.1515 0.0303
>>
矩阵求逆命令:V=inv(A)
5、条件数—衡量奇异程度的量
(1) 在用数值方法计算矩阵的逆时,由于计算中的误差,人们不大可能得到理想的零合理想的全零行,所以矩阵是否奇异,并不是那么绝对的。
(2) 为了评价矩阵接近‘奇异’的程度,采用了‘条件数’(Condition Number)作为常用的衡量指标。它永远大于1。其数值愈接近于1,计算误差愈小。
(3) MATLAB中,条件数用cond(A)计算,它达到10的4次方以上时,求逆的误差就可能相当可观。像现在,条件数达到10的16次方(注:条件数是逆条件数RCOND的倒数),结果是根本不能用的。
6、用矩阵‘除法’解线性方程
(1) 如果m = n,则线性代数方程Ax = b中的A是方阵,设det(A)≠0,则它的逆阵存在。将上式左右同乘以inv(A) ,由于inv(A)*A = I,得到
X = inv(A)*b (1)
MATLAB创立了矩阵除法的概念,因为 inv(A)相当于将A放到分母上去,所以可以把上式写成
X = A \ b (2)
‘\’就称为左除,因为inv(A)是乘在b的左方。
(2) 左除’\’解线性方程的扩展
左除‘\’的功能远远超过了矩阵求逆函数inv,inv(A)函数要求A必须是方阵,所以(1)式只能用来解‘适定’方程,而(2)式并不要求A为方阵,在A是m×n阶且m < n(欠定)时,它只要求A与b的行数相等且A的秩为m。所以(2)式也可以用来解欠定方程,在下例中可以看出。此外,运算符‘\’还能用来解超定方程。
例:左除’\’解欠定方程
A =
3 4 3 2 1
0 6 0 3 3
4 3 4 2 2
1 1 1 0 1
2 6 2 1 3
>> b=[2;3;2;0;1]
b =
2
3
2
0
1
>> x=A\b
Warning: Matrix is singular to working precision.
x =
NaN
NaN
Inf
1.0000
0.0000
>>
得到x=inf,无解。改用行阶梯方法找有效行。左除要求的是系数矩阵的行数与秩相同
A =
3 4 3 2 1
0 6 0 3 3
4 3 4 2 2
1 1 1 0 1
2 6 2 1 3
>> b
b =
2
3
2
0
1
>> B=[A,b]
B =
3 4 3 2 1 2
0 6 0 3 3 3
4 3 4 2 2 2
1 1 1 0 1 0
2 6 2 1 3 1
>> r=rank(B)
r =
4
>> [UB,ip]=rref(B)
UB =
1 0 1 0 0 0
0 1 0 0 0 0
0 0 0 1 0 1
0 0 0 0 1 0
0 0 0 0 0 0
ip =
1 2 4 5
>> U0=UB(1:r,1:5)
U0 =
1 0 1 0 0
0 1 0 0 0
0 0 0 1 0
0 0 0 0 1
>> d=UB(1:4,6)
d =
0
0
1
0
>> x=U0\d
x =
0
0
0
1
0
>>
其中,x是此欠定方程的一个特解。