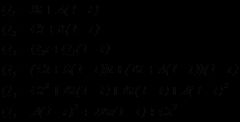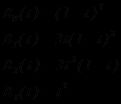Bezier Curves Defined in Parametric Terms

    跟国内大多数计算机辅助几何造型或计算几何的教材不同，《Focus on Curves and Surfaces》介绍Bezier的方法简单，让人易于接受。现将本节内容翻译如下，若有错误，请指出。国内教材上来就是给出定义，而她是按几何方法推导出了二次Bezier曲线的伯恩斯坦（Bernstein）基函数，让人豁然开朗。

==================================================================================================================================================

Bezier曲线的参数方程定义 Bezier Curves Defined in Parametric Terms

原来的CAD/CAM工具和高精度的机器设备、工程师和绘图师绘制的曲线非常粗糙，精度不高。典型地，他们先标记出曲线上很少的几个点，再使用一个曲线板或其它类似的工具画出一条通过这些点的最佳配合的曲线。当引入计算机辅助制造技术后，这种方法就不能接受啦，因为自动化的设备可以制造出高精度的零件。Pierre Bezier在1960年代法国雷诺汽车公司工作时也遇到了这个问题。他发明了Bezier曲线作为高精度拟合曲线的一种方法。计算机驱动的机床设备可以精确地、可靠地的制造出曲线。和其它伟大的发明一样，其他的发明家也同时做出了成绩，但是这种拟合曲线的方法还是以Bezier的名字命名。

注：在第四章，B样条曲线，你将会学到Bezier曲线可以认为是B样条曲线的一个特例。本章中我将用严格的术语来解释，为了后面更通用的B样条曲线。

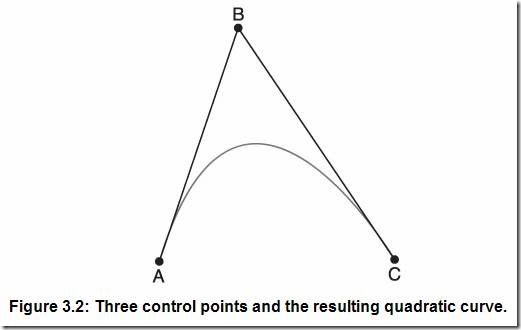
一些推导Bezier曲线的数学概念超出了本书的范围，对于应用的人来说也不是很重要，所以我将用基本的几何术语来描述这个公式。我已经讲过了直线的参数方程，现在将把这些概念扩展到曲线。要画一个线性曲线，至少需要三个点。这三个点叫做控制顶点（Control Points），把控制顶点连接起来就形成了特征多边形（Control Polygon）。图3.2所示为由三个控制顶点形成的二次曲线。

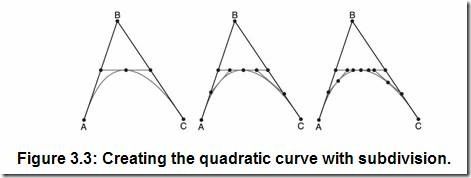
在我讲述怎样用参数方程的方法创建曲线之前，先考虑一个很简单的几何方法。图3.2中的曲线可以用一个基本的细分方法来创建。对每个直线段，选中其中点，并将其相连，重复直到直线段太短而不能再细分时就创建出了光滑的曲线。图3.3所示为使用这种方法的几个步骤：

若你只是画曲线，几何方法完全够用啦。在实际应用中，你很快就会发现这种方法的局限性。如果其中任意一点改变了，你必须重复所有的细分步骤只为了计算出一个点。显然地，你需要一个方法来描述曲线上任意一点，这个方法就是通过控制顶点的方程来实现。这样你只需要计算控制顶点的方程来求出曲线上的点而不需要再用细分方法啦。这听起来你像是参数方程的活！

图3.4与图3.2有着相同的控制顶点，唯一的不同就是通过直线的参数方程来定义点。

现在连接Q1和Q2。图3.5所示为点Q3的参数方程与Q1和Q2的关系。

所以对于参数t的任意值，都可以在每条线段上找到一个与之对应的点，把它们连接上，就找到连接生成的新的直线上的一个点。图3.5中的Q3即是如此。Q3的位置是由参数t和Q1、Q2的方程确定的，即是由A、B、C和t确定。把Q1、Q2的方程代入Q3的方程可以推导出Q3关于控制顶点和参数t的方程。推导过程如下：

方程的最终形式将推导出相同的二次曲线，如图3.2 和3.3。也是二次Bezier曲线的方程。也可以将其看作一系列基函数和相应的控制顶点和乘积。如下方程所示：

由基函数表示的Bezier曲线上的点：

这个基函数就是伯恩斯坦基函数（Bernstein polynomials）。它确定对于任意参数值t，每个控制顶点对曲线的影响。Bezier曲线的控制顶点数也是不定的。对于控制顶点数量确定的伯恩斯坦基函数，可由如下方程求出：

使用更多的控制顶点的缺点就是计算量会随着控制顶点数的增加而增加。所以通常人们会限制控制顶点数为三或四。在三章剩余部分都以四个控制顶点为例，即三次Bezier曲线。其基函数可以上述方程求出，但为了简单其见，列出如下：

三次Bezier曲线的四个基函数：

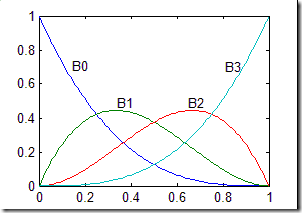
在三章或其它章节中画出基函数有时是很有用的。图3.6所示为四个基函数的图形。参数t的区间是[0,1]，函数值的区间也是[0,1]。

图3.6揭示了Bezier曲线的基函数的几个特性。首先：权性。即所有基函数的和在参数t取任意值时都为1。其次，端点性质。即曲线的端点通过特征多边形的首末点。

图3.6也揭示了Bezier曲线的一些局限性。每个控制顶点都会影响曲线上的点，端点除外。这就意味着在计算曲线上的点时需要计算很多控制顶点。结果就是控制顶点的个数决定了曲线的次数。曲线的次数是控制顶点数减1。改变任意一个控制顶点都会影响到曲线上的点，所以这就是没有局部控制的作用。这也是Bezier的不足之处，在你确定曲线最终形状时有点不够灵活。由于这个原因，人们通常会把几个三次Bezier曲线拼接，而不是用很多控制顶点来形成曲线。