图像白平衡之Gray World Method
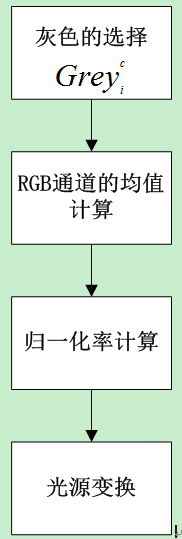
要计算未知光源的特性必须从图片中提取相关的统计特性。当我们能够仅使用一个统计特性就获得未知光源特性时,算法就变得非常简单了。在这种情况下,未知光源必须在整幅图片上都是统一的。均值于是就成为了此类方法之下最好的统计指标。而灰色世界法正是利用了均值作为估算未知光源的关键统计量。
从物理意义上说,灰色世界法假设自然界景物对于光线的平均反射的均值在总体上是个定值,这个定值近似地为“灰色”。在给定图片的白平衡算法中,灰色世界假设图片中的反射面足够丰富,以至于可以作为自然界景物的一个缩影。若这幅图片是在经典光源下拍摄的,其均值就应该等于灰色。若这幅图是在非经典光源下拍摄的,那么均值就会大于或者小于灰色值。而该均值对于灰色的偏离程度则反映了未知光源相对于已知光源的特性。
虽然这个方法比较简单,但是仍然可以从一些方面进行调整。一个方面就是对于灰色的定义形式的选择。包括对于光谱的定义、对于光谱成分的定义和在经典光源之下的 RGB 的响应。另一个更加重要的调整方面就是对于灰色的选择。不管如何定义灰色,最佳的灰色之选必然是自然界实事上出现的灰色。但是这个值是无法获得的(除非是合成数据),所以对于灰色的选择是不同的灰色世界算法的一个重要的区别点。
一个方法是假设这个灰色就是实事上的灰色。也就是说反射光谱是均衡的。给定光源之下的 RGB 响应是纯白色对此光源的响应值的一部分。比方说,可以使用 50%作为反射率(虽然这个灰色值对于人眼视觉习惯而言可能过于明亮)。
另一种方法,就是根据大量的数据提炼出一个均值,并把它定义为灰色。这种方法提炼的灰色值可能因为数据库使用的不同而有所不同。最终提炼的灰色也能仅适用于原始的数据库,而对于数据库未包括的图片的适用度就会比较差一些。确定下来的灰色表达形式可以用 来表示。下标 i 表示信道,上标 c 为canonical 的首字母,表示经典光源。
在确定灰色的表达形式后只要用 RGB 响应与经典光源下灰色的比值来归一化图片就可以了。假设 RGB 响应均值为 Ave_i^u,下标 i 表示信道,上标 U 为Unknown 的首字母,表示未知光源。那么归一化率的计算式为 如下式所示 :
σ_i=(Grey_i^c )/(Ave_i^u )
根据光源转换理论,从未知光源到经典光源下图片表达式的转换式如下式所定义:
那么,灰色世界法的计算过程如下图所示:
Matlab代码如下:
这种是自动寻找RGB均值
clear all;
img=imread('1.jpg');
img=double(img)./256;
r=img(:,:,1);
g=img(:,:,2);
b=img(:,:,3);
avgR = mean(mean(r));
avgG = mean(mean(g));
avgB = mean(mean(b));
avgGray = (avgR + avgG + avgB)/3;
outR = (avgGray/avgR).*r;
outG = (avgGray/avgG).*g;
outB = (avgGray/avgB).*b;
maxRGB = [max(max(outR)) max(max(outG)) max(max(outG))];
factor = max(maxRGB);
outR = outR./factor;
outG = outG./factor;
outB = outB./factor;
GWoutIm(:,:,1) = outR;
GWoutIm(:,:,2) = outG;
GWoutIm(:,:,3) = outB;
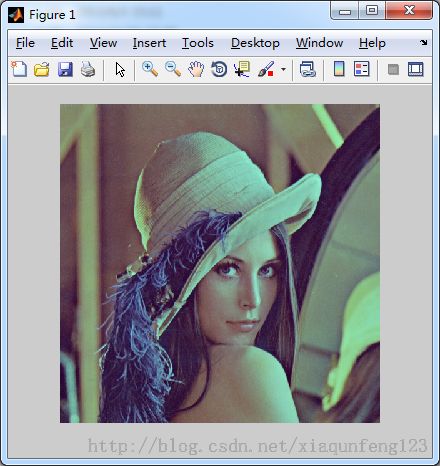
imshow(GWoutIm);原图及效果图如下:
如果想要自定义RGB通道均值,可以采用如下程序:
clear all;
img=imread('hf.png');
r=img(:,:,1);
g=img(:,:,2);
b=img(:,:,3);
aveR=mean(mean(r));
aveG=mean(mean(g));
aveB=mean(mean(b));
qr=200/aveR;
qg=200/aveG;
qb=200/aveB;
img0(:,:,1)=qr*r;
img0(:,:,2)=qg*g;
img0(:,:,3)=qb*b;
imshow(img0);这种方法有时候可以达到一些效果
白平衡后焊缝处的的轮廓更清晰,方便轮廓提取。