android_仿go桌面和点心桌面的球体效果的图片翻页
上半年刚学android那会儿看到go桌面和点心桌面的球体效果时觉得很好看很新鲜,然后脑子想了想是怎么做的:把图标投影到球体上。可球体怎么构建呢?然后上网一通乱搜关于球体的算法,甚至想用墨卡托投影来做,后来仔细想想这个算法用于这个没必要也不现实,并且忙于项目没时间,最后这个效仿球体的demo就没做成。到了下半年的今天,没项目,并且也有时间,脑子一热:球体嘛,做得像球体就行! 然后花了一天把demo给弄出来了,先看效果:
以下几个步骤:
1.切割bitmap成m*n份(m为行数,n为列数)
2.将m*n份bitmap放置到球体上(重点在于如何构建一个球体)
3.跟随手势旋转球体
1.切割bitmap成m*n份
关于如何切割bitmap,这里不作赘述,请看我的上一篇模仿咕噜咕噜的文章http://blog.csdn.net/zhengdongtian/article/details/47606745
2.将m*n份bitmap放置到球体上
要将bitmap放置到球体上,首先得构建一个球体出来。
假设切割bitmap成5*5份。
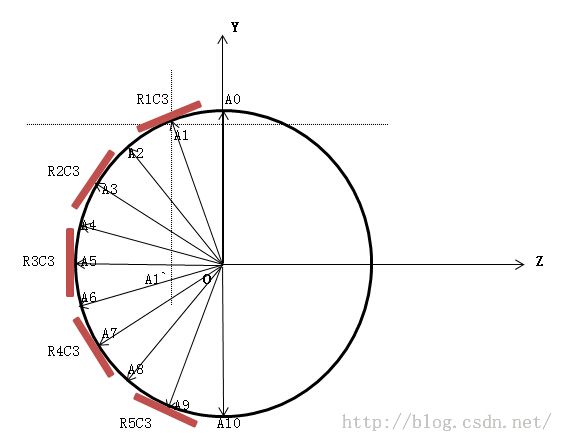
先从camera的角度(x轴,y轴,z轴)来分析这个球,球的中心在原点o(0,0,0)上,沿着zoy一刀切成两半,从右向左观察,如下图:
首先将左半球平均分为10份(2 × m),要将bitmap(R1C3)放在A1,就必须知道A5A1`的长度即z轴上的坐标,A1的竖坐标以及R1C3围绕x轴旋转的度数。
A5A1`的长度 :centerY - R × sin角A1OA0
/**
* bitmap相对于y轴的bitmap的z轴上的距离
* @return
*/
private float[] getCoordZ1(){
float[] coordZ = new float[mRows * mColumns];
double angle = 180.0f / (mRows * 2) * Math.PI / 180;
float centerY = getMeasuredHeight() / 2.0f - getMeasuredHeight() / mRows / 2;
for(int i = 0;i < mRows;i++){
for(int j = 0;j < mColumns;j++){
/**
* x : centerX - cos α * R
* y : centerY - cos α * R
* z : centerY - sin α * R
* rotateX : 90 - α
*/
double realAngle1 = 2 * i * angle + angle;
coordZ[i * mColumns + j] = (float) (centerY - Math.sin(realAngle1) * mRadius);
}
}
return coordZ;
}
A1的竖坐标 :centerY - R × cos角A1OA0
/**
* bitmap所在的y坐标
* @return
*/
private float[] getCoordY(){
float[] coordY = new float[mRows * mColumns];
double angle = 180.0f / (mRows * 2) * Math.PI / 180;
float centerY = getMeasuredHeight() / 2.0f - getMeasuredHeight() / mRows / 2;
for(int i = 0;i < mRows;i++){
for(int j = 0;j < mColumns;j++){
/**
* x : centerX - cos α * R
* y : centerY - cos α * R
* z : centerY - sin α * R
* rotateX : 90 - α
*/
double realAngle = 2 * i * angle + angle;
coordY[i * mColumns + j] = (float) (centerY - Math.cos(realAngle) * mRadius);
}
}
return coordY;
}
围绕x轴旋转的度数 :90 - 角A1OA0
/**
* bitmap围绕x轴旋转多少度
* @return
*/
private float[] getRotateX(){
float[] rotateX = new float[mRows * mColumns];
double angle = 180.0f / (mRows * 2) * Math.PI / 180;
for(int i = 0;i < mRows;i++){
for(int j = 0;j < mColumns;j++){
/**
* x : centerX - cos α * R
* y : centerY - cos α * R
* z : centerY - sin α * R
* rotateX : 90 - α
*/
double realAngle = 2 * i * angle + angle;
rotateX[i * mColumns + j] = (float) (90 - (realAngle / (Math.PI / 180)));
}
}
return rotateX;
}
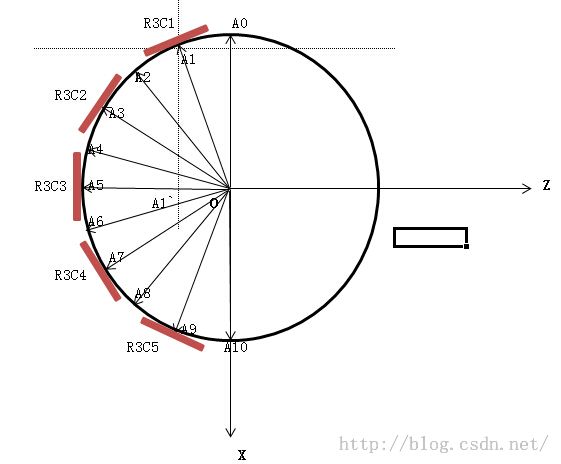
bitmap(R3C1)的横坐标 :centerX - cos角A1OA0 × R
bitmap(R3C1)的Z轴坐标 :centerY - sin角A1OA0 × R
bitmap(R3C1)围绕y轴旋转的度数 :角A1OA0 × R - 90
根据上面只求出了前半球,而后半球还未构建出来。其实我们的球只能水平方向转动,所以后半球只需要将前半球转动180度即可求得。
所以上面的三个公式得稍作改动,需要加上起始角度。
bitmap(R3C1)的横坐标 :centerX - cos(角A1OA0 × R + 起始角度)
/**
* bitmap所在的x坐标
* @param startAngle
* @return
*/
private float[] getCoordX(double startAngle){
float[] coordX = new float[mRows * mColumns];
double angle = 180.0f / (mColumns * 2) * Math.PI / 180;
float centerX = getMeasuredWidth() / 2.0f - getMeasuredWidth() / mColumns / 2;
for(int i = 0;i < mRows;i++){
for(int j = 0;j < mColumns;j++){
/**
* x : centerX - cos α * R
* y : centerY - cos α * R
* z : centerY - sin α * R
* rotateX : 90 - α
*/
double realAngle = 2 * j * angle + angle + startAngle * Math.PI / 180;
coordX[i * mColumns + j] = (float) (centerX - Math.cos(realAngle) * mRadius);
}
}
return coordX;
}
bitmap(R3C1)的Z轴坐标 :centerY - sin(角A1OA0 × R + 起始角度)
/**
* bitmap相对于x轴的bitmap的z轴上的距离
* @param startAngle
* @return
*/
private float[] getCoordZ2(double startAngle){
float[] coordZ = new float[mRows * mColumns];
double angle = 180.0f / (mColumns * 2) * Math.PI / 180;
float centerY = getMeasuredHeight() / 2.0f - getMeasuredHeight() / mRows / 2;
for(int i = 0;i < mRows;i++){
for(int j = 0;j < mColumns;j++){
/**
* x : centerX - cos α * R
* y : centerY - cos α * R
* z : centerY - sin α * R
* rotateX : 90 - α
*/
double realAngle = 2 * j * angle + angle + startAngle * Math.PI / 180;
coordZ[i * mColumns + j] = (float) (centerY - Math.sin(realAngle) * mRadius);
}
}
return coordZ;
}
bitmap(R3C1)围绕y轴旋转的度数 :(角A1OA0 × R + 起始角度) - 90
/**
* bitmap围绕y轴旋转多少度
* @param startAngle
* @return
*/
private float[] getRotateY(double startAngle){
float[] rotateY = new float[mRows * mColumns];
double angle = 180.0f / (mColumns * 2) * Math.PI / 180;
for(int i = 0;i < mRows;i++){
for(int j = 0;j < mColumns;j++){
/**
* x : centerX - cos α * R
* y : centerY - cos α * R
* z : centerY - sin α * R
* rotateX : 90 - α
*/
double realAngle = 2 * j * angle + angle + startAngle * Math.PI / 180;
rotateY[i * mColumns + j] = (float) ((realAngle / (Math.PI / 180)) - 90);
}
}
return rotateY;
}
其他bitmap同理。
需要注意的一点是,由于满屏的bitmap切割后再组成球,难免造成bitmap之间的重叠导致整体不好看。所以将bitmap按照一定规则缩小后组成球。
3.跟随手势旋转球体
球体旋转时涉及到绘制bitmap的顺序,因为当我从左往右滑动时,我绘制bitmap的顺序是(以第一行举例)R1C1,R1C2。。。R1C5,当球旋转了一定角度后R1C5跑到
后半球去了,本应是R1C4挡住R1C5,但是由于先画R1C4后画R1C5,所以R1C5会挡住R1C4。
@Override
protected void onDraw(Canvas canvas) {
//canvas.drawColor(0xFFAAAAAA);
deltaDistance = mTouch.x - mFirstTouch.x;
if(deltaDistance < 0.0f){
if(deltaDistance > -2.0f) {
deltaDistance = 0.0f;
}
}else{
if(deltaDistance < 2.0f) {
deltaDistance = 0.0f;
}
}
if(!isCurrentFirst){
if(mNextPageBitmap != null){
//后半球
drawNextPageArea(canvas, mNextPageBitmap);
}
//前半球
drawCurPageArea(canvas, mCurPageBitmap);
}else{
//前半球
drawCurPageArea(canvas, mCurPageBitmap);
if(mNextPageBitmap != null){
//后半球
drawNextPageArea(canvas, mNextPageBitmap);
}
}
}
代码
https://github.com/skypanda100/Sphere
http://download.csdn.net/detail/zhengdongtian/9023059