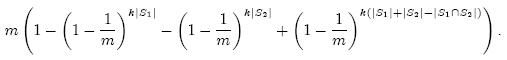应用Bloom Filter的几个小技巧
原文地址:http://hi.baidu.com/xdzhang_china/blog/item/2847777e83fb020229388a15.html
下面列举几个基于标准 Bloom Filter 的小技巧:
1. 求两个集合的并。假设有两个 Bloom Filter 分别表示集合 S1 和 S2 ,它们位数组的大小相同且使用同一组哈希函数,那么要求表示 S1 和 S2 并集的 Bloom Filter ,只要将 S1 和 S2 的位数组进行“或”操作即可得到 结果。
2. 将 Bloom Filter “对 折”。 如果想将一个 Bloom Filter 的大小缩小一半,那么只需将 Bloom Filter 的位数组分成两半进行“或”操作, 得到的结果即为所求。在查找某一元素时,需要将哈希后的索引地址的最高位屏蔽掉。
3. 通过 0 的 数目估计集合元素个数。在第一篇文章 Bloom Filter 概念 和原理 中,我们提到过: 位数组中 0 的比例非常集中地分布在它的数学期望值 m (1 - 1/m)kn 的附近,其 中 m 为位数组的大小, k 为哈希函数的个数, n 为 Bloom Filter 所 表示集 合的元素个数。根据上式,知道了 0 的 个数就可以很容易推断 n 的 大小。
4. 通过内积估计集合交集元素个数。假设有两个 Bloom Filter 分别表示集合 S1 和 S2 ,它们位数组的大小相同且使用同 一组哈希函数,下面我们来看第 i 位 在两个 Bloom Filter 同 时被置为 1 的概率。要 让某一位同时被置为 1 , 只有两种可能:要么它是被 S1 ∩S2 中 的元素设置的,要么分别是被 S1 – (S1 ∩S2 ) 和 S2 - (S1 ∩S2 ) 中 的元素设置的。因此第 i 位 在两个 Bloom Filter 同 时被置为 1 的概率为:
|S| 表示 S 中元素的个数, k 表示哈希函数的个数, m 表示位数组的大小。经过化简,再乘以 m ,得到两个位数组内积的数学期望值为:
如 果不知道 |S1 | 和 |S2 | ,可以用 3 中的方法根据 0 的个数估计出它们的大小。最后,根据上式,我们在知道内积的 情况下就可以很容易推断 | S1 ∩S2 | 的 大小。
5. 表 示全集。很简单,将位数组设为全 1 就 可以表示全集了,因为查找任何一个元素都会得到肯定的结果。
Counting Bloom Filter
从前面几篇对 Bloom Filter 的介绍可以看出,标准的 Bloom Filter 是一种很简单的数据结构,它只支持插入和查找两种操作。在所要表达的集 合是静态集合的时候,标准 Bloom Filter 可 以很好地工作,但是如果要表达的集合经常变动,标准 Bloom Filter 的弊端就显现出来了,因为它不支持删除操作。
Counting Bloom Filter 的 出现解决了这个问题,它将标准 Bloom Filter 位 数组的每一位扩展为一个小的计数器( Counter ), 在插入元素时给对应的 k ( k 为哈希函数个数)个 Counter 的值分别加 1 ,删除元素时给对应的 k 个 Counter 的值分别减 1 。 Counting Bloom Filter 通 过多占用几倍的存储空间的代价,给 Bloom Filter 增 加了删除操作。下一个问题自然就是,到底要多占用几倍呢?
我们先计算第 i 个 Counter 被增加 j 次的概率,其中 n 为集合元素个数, k 为哈希函数个数, m 为 Counter 个数(对应着原来位数组的大小):
上 面等式右端的表达式中,前一部分表示从 nk 次 哈希中选择 j 次,中间 部分表示 j 次哈希都选 中了第 i 个 Counter ,后一部分表示其它 nk – j 次哈希都没有选中第 i 个 Counter 。因此,第 i 个 Counter 的值大于 j 的概率可以限定为:
上 式第二步缩放中应用了估计阶乘的斯特林公式:
在 Bloom Filter 概念和 原理 一文中,我们提到过 k 的 最优值为 (ln2)m/n , 现在我们限制 k ≤ (ln2)m/n , 就可以得到如下结论:
如 果每个 Counter 分 配 4 位,那么当 Counter 的值达到 16 时就会溢出。这个概率为:
这 个值足够小,因此对于大多数应用程序来说, 4 位 就足够了。
关 于Counting Bloom Filter最早的论文:Summary Cache: A Scalable Wide-Area Web Cache Sharing Protocol