离圆心最远的整数点(微软笔试题)
题目链接:http://hihocoder.com/contest/mstest2015sept2/problem/1
题目:
题目1 : Farthest Point
- 样例输入
-
1.000 1.000 5.000
- 样例输出
-
6 1
描述
Given a circle on a two-dimentional plane.
Output the integral point in or on the boundary of the circle which has the largest distance from the center.
输入
One line with three floats which are all accurate to three decimal places, indicating the coordinates of the center x, y and the radius r.
For 80% of the data: |x|,|y|<=1000, 1<=r<=1000
For 100% of the data: |x|,|y|<=100000, 1<=r<=100000
输出
One line with two integers separated by one space, indicating the answer.
If there are multiple answers, print the one with the largest x-coordinate.
If there are still multiple answers, print the one with the largest y-coordinate.
分析:
这一题是微软的一道笔试题,笔试题中微软的笔试题是最经典也是难度选择很恰当(有难度但不是变态的那种难的)的,先给个好评。
这一条道题是给定圆心坐标和半径长度,要你求出离圆心最远的整数点,输出其中x最大的点,不唯一则输出y最大的点。
要找出圆内距离圆心最大的点,并且要是整数点,比较先想到的就是对于区间[x - r, x + r]和[y - r, y +r]上的点进行遍历,找出其中在圆上或圆内距离圆心最大的坐标点。
但是,很明显,对于r很大的情况,以上情况会超时。
其实,距离圆心最远的点,肯定是在圆周的周围,我们只要遍历圆周周围(并且不在园外)的点即可,没有必要把圆内部的点都遍历。
那么,我们可以先对x轴遍历,从[x + r, x + r]内的每个整数点x遍历,然后找出当前x点对应的非圆外的y最大值和最小值,进行判断是否是最远点。
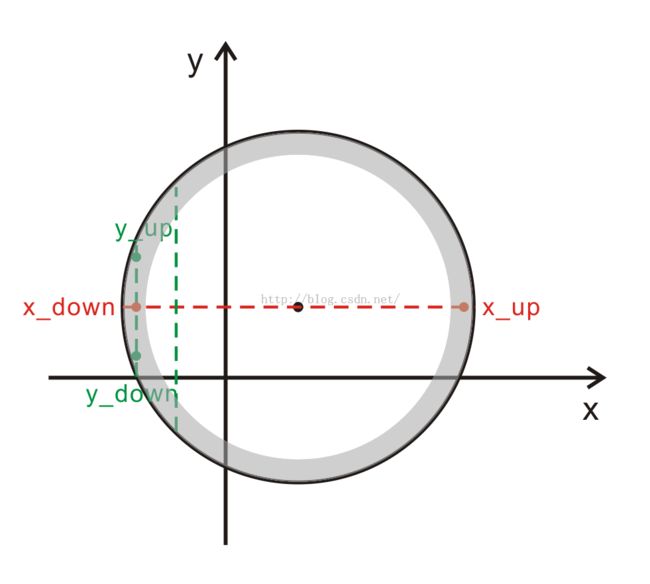
如下图:
这样,我们遍历的点数最多也就是2*r*2=4r个。遍历的范围相当于图中的灰色圆环区域。
接下来的问题就是怎么取到符合范围的整数点的问题,在圆内的点,不论是对于x轴还是y轴,
如果是取其max,那么都需要向下靠拢,即如果x + r是1.1,那么我们的x_max只能取1,如果算出来的y是-1.1,那么我们的y_max只能取-2,
而取min则要向上靠拢,即如果x - r是1.1,那么我们的x_min只能取2,如果算出来的y是-1.1,那么我们的y_min只能取-1,
而普通的int()是无法做到这一点,这里我们需要一个地板和天花板函数floor和ceil,具体请看下面表格:
|
类别
|
x = 1.1
|
x = -1.1
|
性质
|
|
int(x)
|
1
|
-1
|
向0靠
|
|
floor(x)
|
1
|
-2
|
向下(小数)靠 |
|
ceil(x)
|
2
|
-1
|
向上(大树)靠 |
#include <iostream>
#include <cmath>
using namespace std;
int main(){
cout << "int (1.1) = " << int(1.1) << "\t";
//int是向0靠
cout << "int (-1.1) = " << int(-1.1) << endl;
cout << "floor (1.1) = " << floor(1.1) << "\t";
//floor是下靠
cout << "floor (-1.1) = " << floor(-1.1) << endl;
cout << "ceil (1.1) = " << ceil(1.1) << "\t";
//ceil是想上靠
cout << "ceil (-1.1) = " << ceil(-1.1) << endl;
return 0;
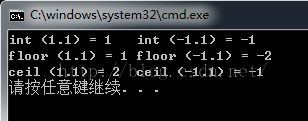
}结果如下:
AC代码:
#include <iostream>
#include <string>
#include <cmath>
using namespace std;
int main(){
double x, y, r;
cin >> x >> y >> r;
double distance = 0;
int result_x, result_y;
for (double i = floor(x + r); i >= ceil(x - r); --i){//*point:floor,ceil
int y_up = floor(y + sqrt(r*r - (x - i)*(x - i)));//确定x对应的y的上限
int y_down = ceil(y - sqrt(r*r - (x - i)*(x - i)));//确定y的下限
if (y_up < y_down) swap(y_up, y_down);//当差距很小的时候,会有up < down的情况
double distance_up = (i - x)*(i - x) + (y_up - y)*(y_up - y);
double distance_down = (i - x)*(i - x) + (y_down - y)*(y_down - y);
if (distance_up>distance && distance_up <= r*r || distance_up == distance && (i > result_x || (i == result_x && y_up > result_y))){
//最远点&&在圆内/上,或者是x或者y更优
distance = distance_up;
result_x = i;
result_y = y_up;
}
if (distance_down>distance && distance_down <= r*r || distance_down == distance && (i > result_x || (i == result_x && y_down > result_y))){
//最远点&&在圆内/上,或者是x或者y更优
distance = distance_down;
result_x = i;
result_y = y_down;
}
}
cout << result_x << " " << result_y << endl;
return 0;
}
——Apie陈小旭