POJ 1673 EXOCENTER OF A TRIANGLE
EXOCENTER OF A TRIANGLE
| Time Limit: 1000MS | Memory Limit: 10000K | |
| Total Submissions: 1853 | Accepted: 682 |
Description
Given a triangle ABC, the Extriangles of ABC are constructed as follows:
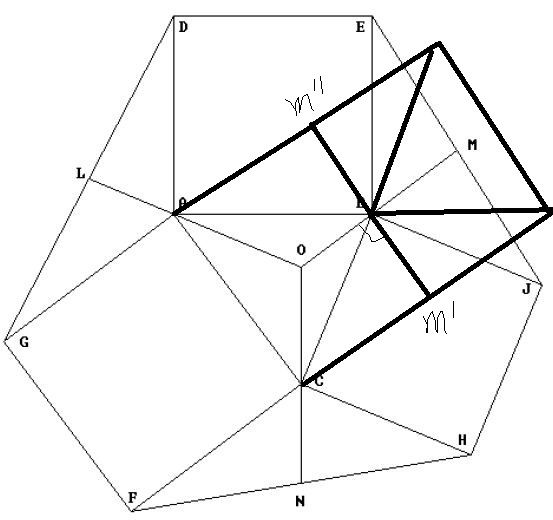
On each side of ABC, construct a square (ABDE, BCHJ and ACFG in the figure below).
Connect adjacent square corners to form the three Extriangles (AGD, BEJ and CFH in the figure).
The Exomedians of ABC are the medians of the Extriangles, which pass through vertices of the original triangle,extended into the original triangle (LAO, MBO and NCO in the figure. As the figure indicates, the three Exomedians intersect at a common point called the Exocenter (point O in the figure).
This problem is to write a program to compute the Exocenters of triangles.

On each side of ABC, construct a square (ABDE, BCHJ and ACFG in the figure below).
Connect adjacent square corners to form the three Extriangles (AGD, BEJ and CFH in the figure).
The Exomedians of ABC are the medians of the Extriangles, which pass through vertices of the original triangle,extended into the original triangle (LAO, MBO and NCO in the figure. As the figure indicates, the three Exomedians intersect at a common point called the Exocenter (point O in the figure).
This problem is to write a program to compute the Exocenters of triangles.

Input
The first line of the input consists of a positive integer n, which is the number of datasets that follow. Each dataset consists of 3 lines; each line contains two floating point values which represent the (two -dimensional) coordinate of one vertex of a triangle. So, there are total of (n*3) + 1 lines of input. Note: All input triangles wi ll be strongly non-degenerate in that no vertex will be within one unit of the line through the other two vertices.
Output
For each dataset you must print out the coordinates of the Exocenter of the input triangle correct to four decimal places.
Sample Input
2 0.0 0.0 9.0 12.0 14.0 0.0 3.0 4.0 13.0 19.0 2.0 -10.0
Sample Output
9.0000 3.7500 -48.0400 23.3600
Source
Greater New York 2003
所求点位垂心的证明可以参考下面这张图,主要通过三角形的旋转来证明
//判断三角形垂心问题 #include <iostream> #include <cmath> #define EPS 1e-8 //精度是关键 struct node { double x, y; }; struct line { node n1, n2; }; node intersection(line u,line v){ double a1, b1, c1, a2, b2, c2; a1 = u.n2.y - u.n1.y; b1 = u.n1.x - u.n2.x; c1 = u.n2.x * u.n1.y - u.n2.y * u.n1.x; a2 = v.n2.y - v.n1.y; b2 = v.n1.x - v.n2.x; c2 = v.n2.x * v.n1.y - v.n2.y * v.n1.x; node res; //这里之所以可以直接除,是因为两条线不可能平行,因此分母不可能为0 //所以这个函数不适合平行的两条直线 //由于这里确定两条直线会相交所以可以放心使用,一般情况下的处理方法是: //先判断两直线斜率是否相同,如果相同则单独处理,不调用intersection()函数,然后用叉积判断两直线是否重合。这 //样就可以得到两直线的三种关系(相交,(重合,平行)) res.x = (b1 * c2 - b2 * c1) / (a1 * b2 - a2 * b1); res.y = (a1 * c2 - a2 * c1) / (a2 * b1 - a1 * b2); /*要加精度啊,WA N次,之所以要加EPS,是因为编译器很可能产生0 / x = -0.0000之类的情况*/ if(fabs(res.x) < EPS) res.x = 0; if(fabs(res.y) < EPS) res.y = 0; return res; } //计算垂心 node getEXO(const node &n1, const node &n2, const node &n3) { node nt1; line l1; nt1.x = n1.x - n3.y + n2.y; nt1.y = n1.y + n3.x - n2.x; l1.n1 = n1; l1.n2 = nt1; node nt2; line l2; nt2.x = n2.x + n3.y - n1.y; nt2.y = n2.y - n3.x + n1.x; l2.n1 = n2; l2.n2 = nt2; node EXO; //getInter(l1, l2, EXO); EXO = intersection(l1, l2); return EXO; } int main() { int caseNum; double x1, y1, x2, y2, x3, y3; scanf("%d", &caseNum); while(caseNum--) { scanf("%lf%lf%lf%lf%lf%lf", &x1, &y1, &x2, &y2, &x3, &y3); node n1, n2, n3; n1.x = x1; n1.y = y1;n2.x = x2; n2.y = y2; n3.x = x3; n3.y = y3; node EXO = getEXO(n1, n2, n3); printf("%0.4lf %0.4lf/n", EXO.x, EXO.y); } return 0; }