hdu 4472 Count

Count

Time Limit: 2000/1000 MS (Java/Others)    Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 669    Accepted Submission(s): 432

Problem Description

Prof. Tigris is the head of an archaeological team who is currently in charge of an excavation in a site of ancient relics.
This site contains relics of a village where civilization once flourished. One night, examining a writing record, you find some text meaningful to you. It reads as follows.
“Our village is of glory and harmony. Our relationships are constructed in such a way that everyone except the village headman has exactly one direct boss and nobody will be the boss of himself, the boss of boss of himself, etc. Everyone expect the headman is considered as his boss’s subordinate. We call it relationship configuration. The village headman is at level 0, his subordinates are at level 1, and his subordinates’ subordinates are at level 2, etc. Our relationship configuration is harmonious because all people at same level have the same number of subordinates. Therefore our relationship is …”
The record ends here. Prof. Tigris now wonder how many different harmonious relationship configurations can exist. He only cares about the holistic shape of configuration, so two configurations are considered identical if and only if there’s a bijection of n people that transforms one configuration into another one.
Please see the illustrations below for explanation when n = 2 and n = 4.

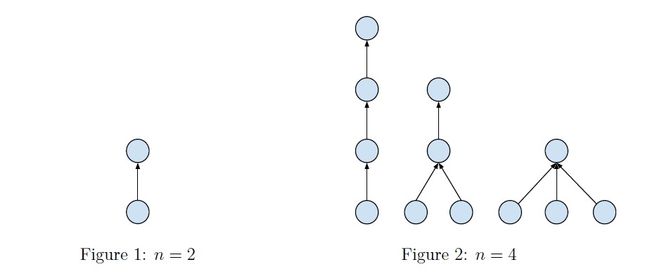
The result might be very large, so you should take module operation with modules 10 ⁹ +7 before print your answer.

 

Input

There are several test cases.
For each test case there is a single line containing only one integer n (1 ≤ n ≤ 1000).
Input is terminated by EOF.

 

Output

For each test case, output one line “Case X: Y” where X is the test case number (starting from 1) and Y is the desired answer.

 

Sample Input

   
   
   
   

    
    
    
    1
2
3
40
50
600
700
   
   
   
   

 

Sample Output

   
   
   
   

    
    
    
    Case 1: 1
Case 2: 1
Case 3: 2
Case 4: 924
Case 5: 1998
Case 6: 315478277
Case 7: 825219749
   
   
   
   

 

Source

2012 Asia Chengdu Regional Contest

 

Recommend

liuyiding

 

第二次积分赛题目。比赛时没看这题。下来后无比悔恨其实就是一道很水的dp。自己下来不到十分钟就A了。哎。。

下次一定不放过任何水题了。。

首先是自己的思路：自己画了几个图后。发现了一些规律。那就是每层的节点数必须相同。于是直接可以按层转移。

我们定义图形节点数为i时叶子结点数为j时的方法数。然后我们枚举下一层的叶子结点数k。然后可得

dp[i+k*j][j*k]+=dp[i][j]。

代码如下：

#include <iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
__int64 dp[1005][1010],ans;
int main()
{
    int i,j,k,n,cas=1;

    memset(dp,0,sizeof dp);
    dp[1][1]=1;
    for(i=1;i<=1000;i++)
    {
        for(j=1;j<=i;j++)
        {
            for(k=1;i+k*j<=1000;k++)
                dp[i+k*j][j*k]+=dp[i][j];
        }
    }
    while(~scanf("%d",&n))
    {
        ans=0;
        for(i=1;i<=n;i++)
            ans+=dp[n][i];
        printf("Case %d: %I64d\n",cas++,ans%(1000000000+7));
    }
    return 0;
}

进一步分析可以更简单。问题可以抽象成去掉根结点后剩下的结点分成相同的部分的方法数。那么

dp[i]代表结点数为i的方法数。dp[i]+=dp[k]。(i-1)%k==0。原理很简单一个节点一定要用去做树根，所以剩下i-1个点，这i-1个节点把它分成几份，这几份完全相同，其本身完全对称，然后不断更新就行了。

#include <iostream>
#include<string.h>
#include<stdio.h>
using namespace std;
__int64 dp[1005];
int main()
{
    int i,j,n,cas=1;

    memset(dp,0,sizeof dp);
    dp[1]=1;
    for(i=1;i<=1000;i++)
    {
        for(j=1;j<i;j++)
        {
            if((i-1)%j==0)
                dp[i]+=dp[j];
        }
    }
    while(~scanf("%d",&n))
        printf("Case %d: %I64d\n",cas++,dp[n]%(1000000000+7));
    return 0;
}