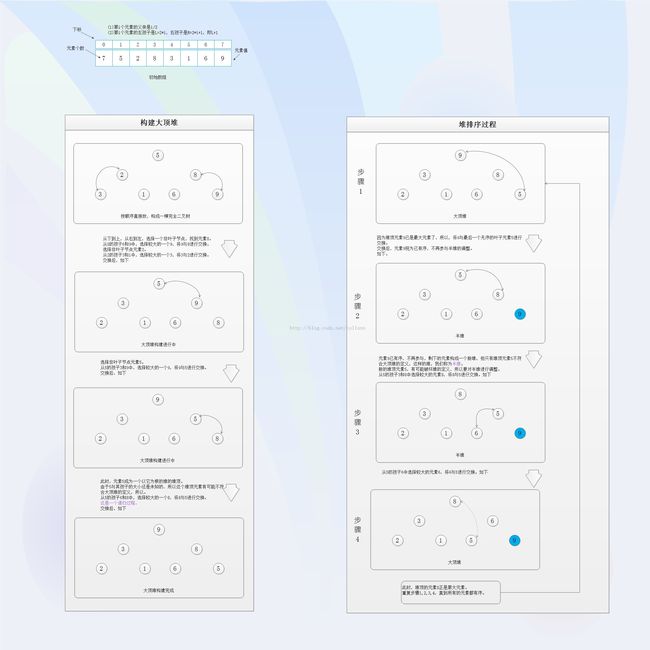
堆排序，大顶堆，小顶堆

一如既往，先上详细的过程图。

应用场景

比如求10亿个数中的最大的前10个数，时时构建只有10个元素的小顶堆，如果比堆顶小，则不处理；如果比堆顶大，则替换堆顶，然后依次下沉到适当的位置。

比如求10亿个数中的最小的前10个数，时时构建只有10个元素的大顶堆，如果比堆顶大，则不处理；如果比堆顶小，则替换堆顶，然后依次下沉到适当的位置。

代码如下，有详细的注释

package com.collonn.algorithm.sort;

/**
 * <pre>
 * 	堆排序基本步骤，假设没有重复的元素
 * 	空间：为O(1)
 * 	时间：N*logN
 * 
 * 	步骤1：构建大顶堆(或小顶堆)
 * 	步骤2：将 堆顶 元素 与 未排序 的最后一个叶子，进行交换
 * 	步骤3：并对半堆进行修正(不考虑已有序的叶子)
 * 	步骤4：重复步骤2,3
 * </pre>
 */
public class HeapSort {
	/**
	 * <pre>
	 * 构建大顶堆，假设没有重复的元素
	 * 1：下标为0的元素，表示元素数量，从下标1开始表示元素值，这样做的原因仅仅是为了更方便的计算，往下看
	 * 2：最初，数组中的值，从下标1开始到数组末尾，表示一个完全二叉树的顺序存储
	 * 3：那么可以得出以下位置关系：
	 * 		(1)第i个元素的父亲是i/2
	 * 		(2)第i个元素的左孩子是L=2*i，右孩子是R=2*i+1，即L+1
	 * 4：假如最后一个元素的下标是i，其双亲下标为j=i/2，我们依次对[1,j]的元素进行堆构建即可
	 * </pre>
	 */
	public void initHeap(int[] s) {
		// 最后一个叶子的双亲下标
		int lastParentIndex = s[0] / 2;

		// 对半堆进行修正
		for (int i = lastParentIndex; i > 0; i--) {
			this.reBuild(i, s, s[0]);
		}
	}

	/**
	 * <pre>
	 * 对半堆进行修正，半堆的意思是：除堆顶元素外，其它元素都符合堆定义
	 * </pre>
	 * 
	 * @param i 部分元素组成的堆的堆顶
	 * @param s 元素数组
	 * @param last 未排序的元素下标
	 */
	private void reBuild(int i, int[] s, int last) {
		System.out.printf("\n-------------------- rebuild --------------------");
		System.out.printf("\ni=%d，s[i]=%d, last=%d", i, s[i], last);
		// 下标为i的左孩子下标
		int L = 2 * i;
		// 下标为i的右孩子下标
		int R = L + 1;
		// 左右孩子中较小的一个
		int minLR = -1;

		// 下标为i的元素没有孩子
		if (L > last && R > last) {
			System.out.printf("\nno children");
			return;
		}

		// 下标为i的元素只有左孩子
		if (L <= last && R > last) {
			minLR = L;
		}

		// 下标为i的元素只有右孩子
		if (L > last && R <= last) {
			minLR = R;
		}

		// 下标为i的元素有两个孩子
		if (L <= last && R <= last) {
			minLR = s[L] < s[R] ? R : L;
		}

		System.out.printf("\nminLr=%d, s[minLR]=%d", minLR, s[minLR]);

		// 比较以下三个元素，双亲，双亲的左孩子，双亲的右孩子
		if (s[i] > s[minLR]) {
			System.out.printf("\n i=%d, s[i]=%d is the max one.", i, s[i]);
			return;
		} else {
			this.swap(i, minLR, s);
			// 递归进行堆调整
			this.reBuild(minLR, s, last);
		}
	}

	// 元素交换
	private void swap(int i, int j, int[] s) {
		System.out.printf("\nswap, i=%d, s[i]=%d, j=%d, s[j]=%d", i, s[i], j, s[j]);
		int t = s[i];
		s[i] = s[j];
		s[j] = t;
	}

	/**
	 * <pre>
	 * 堆排序
	 * 1：将 堆顶 元素 与 未排序 的最后一个叶子交换(这个交换后的叶子已是有序的，后面的堆调整，不再考虑这个叶子元素了)
	 * 2：将堆顶元素按照堆定义，依次进行下沉，直到新堆符合堆定义
	 * 3：重复1,2
	 * </pre>
	 * 
	 * @param s
	 */
	public void heapSort(int[] s) {
		System.out.printf("\n---------------------- heapSort ----------------------");
		for (int j = s[0]; j > 0; j--) {
			System.out.printf("\n找到最小值:%d", s[1]);
			this.swap(1, j, s);
			PrintArray(s);
			this.reBuild(1, s, j - 1);
			PrintArray(s);
		}
	}

	// 打印数组
	private static void PrintArray(int[] s) {
		System.out.printf("\n-----------------------------------");
		System.out.printf("\n下标:");
		for (int p = 0; p < s.length; p++) {
			System.out.printf("%2d,", p);
		}
		System.out.print("\n值值:");
		for (Integer m : s) {
			System.out.printf("%2d,", m);
		}
	}

	public static void main(String[] args) {
		// int[] s = new int[] { 99, 88, 5, 99, 7, 9, 3, 8, 10, 90, 56, 83, 39, 22 };
		int[] s = new int[] { 7, 5, 2, 8, 3, 1, 6, 9 };
		PrintArray(s);

		HeapSort heapSort = new HeapSort();
		heapSort.initHeap(s);
		PrintArray(s);
		heapSort.heapSort(s);

		PrintArray(s);
	}

}

输出如下：

-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 5, 2, 8, 3, 1, 6, 9,
-------------------- rebuild --------------------
i=3，s[i]=8, last=7
minLr=7, s[minLR]=9
swap, i=3, s[i]=8, j=7, s[j]=9
-------------------- rebuild --------------------
i=7，s[i]=8, last=7
no children
-------------------- rebuild --------------------
i=2，s[i]=2, last=7
minLr=4, s[minLR]=3
swap, i=2, s[i]=2, j=4, s[j]=3
-------------------- rebuild --------------------
i=4，s[i]=2, last=7
no children
-------------------- rebuild --------------------
i=1，s[i]=5, last=7
minLr=3, s[minLR]=9
swap, i=1, s[i]=5, j=3, s[j]=9
-------------------- rebuild --------------------
i=3，s[i]=5, last=7
minLr=7, s[minLR]=8
swap, i=3, s[i]=5, j=7, s[j]=8
-------------------- rebuild --------------------
i=7，s[i]=5, last=7
no children
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 9, 3, 8, 2, 1, 6, 5,
---------------------- heapSort ----------------------
找到最小值:9
swap, i=1, s[i]=9, j=7, s[j]=5
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 5, 3, 8, 2, 1, 6, 9,
-------------------- rebuild --------------------
i=1，s[i]=5, last=6
minLr=3, s[minLR]=8
swap, i=1, s[i]=5, j=3, s[j]=8
-------------------- rebuild --------------------
i=3，s[i]=5, last=6
minLr=6, s[minLR]=6
swap, i=3, s[i]=5, j=6, s[j]=6
-------------------- rebuild --------------------
i=6，s[i]=5, last=6
no children
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 8, 3, 6, 2, 1, 5, 9,
找到最小值:8
swap, i=1, s[i]=8, j=6, s[j]=5
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 5, 3, 6, 2, 1, 8, 9,
-------------------- rebuild --------------------
i=1，s[i]=5, last=5
minLr=3, s[minLR]=6
swap, i=1, s[i]=5, j=3, s[j]=6
-------------------- rebuild --------------------
i=3，s[i]=5, last=5
no children
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 6, 3, 5, 2, 1, 8, 9,
找到最小值:6
swap, i=1, s[i]=6, j=5, s[j]=1
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 1, 3, 5, 2, 6, 8, 9,
-------------------- rebuild --------------------
i=1，s[i]=1, last=4
minLr=3, s[minLR]=5
swap, i=1, s[i]=1, j=3, s[j]=5
-------------------- rebuild --------------------
i=3，s[i]=1, last=4
no children
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 5, 3, 1, 2, 6, 8, 9,
找到最小值:5
swap, i=1, s[i]=5, j=4, s[j]=2
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 2, 3, 1, 5, 6, 8, 9,
-------------------- rebuild --------------------
i=1，s[i]=2, last=3
minLr=2, s[minLR]=3
swap, i=1, s[i]=2, j=2, s[j]=3
-------------------- rebuild --------------------
i=2，s[i]=2, last=3
no children
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 3, 2, 1, 5, 6, 8, 9,
找到最小值:3
swap, i=1, s[i]=3, j=3, s[j]=1
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 1, 2, 3, 5, 6, 8, 9,
-------------------- rebuild --------------------
i=1，s[i]=1, last=2
minLr=2, s[minLR]=2
swap, i=1, s[i]=1, j=2, s[j]=2
-------------------- rebuild --------------------
i=2，s[i]=1, last=2
no children
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 2, 1, 3, 5, 6, 8, 9,
找到最小值:2
swap, i=1, s[i]=2, j=2, s[j]=1
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 1, 2, 3, 5, 6, 8, 9,
-------------------- rebuild --------------------
i=1，s[i]=1, last=1
no children
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 1, 2, 3, 5, 6, 8, 9,
找到最小值:1
swap, i=1, s[i]=1, j=1, s[j]=1
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 1, 2, 3, 5, 6, 8, 9,
-------------------- rebuild --------------------
i=1，s[i]=1, last=0
no children
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 1, 2, 3, 5, 6, 8, 9,
-----------------------------------
下标: 0, 1, 2, 3, 4, 5, 6, 7,
值值: 7, 1, 2, 3, 5, 6, 8, 9,

原创博文，转载请注明出处。