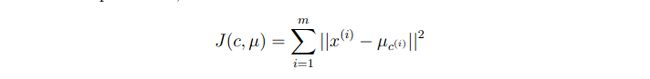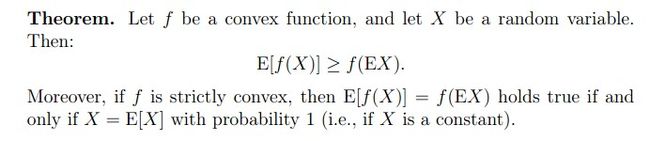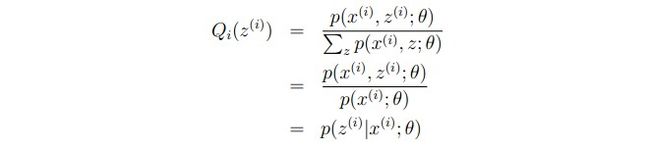机器学习 cs229学习笔记2 (k-means,EM & Mixture of Gaussians)
(all is based on stanford's opencourse cs229 lecture 12)
首先介绍的是聚类算法中最简单的K-Means算法
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
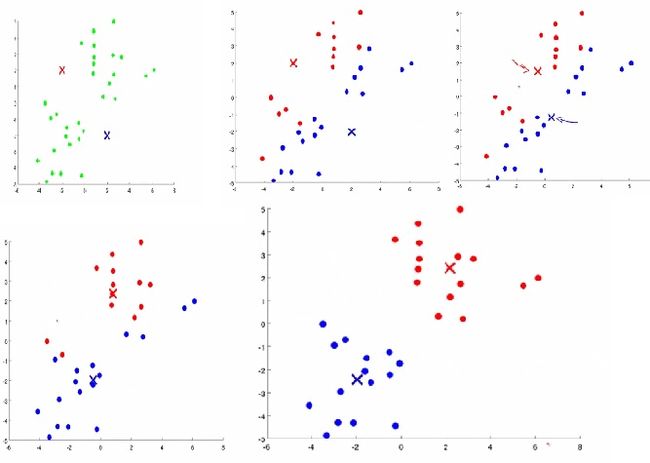
算法的实质就是:(随机初始化聚点)
1、将样例的每个点分配给离它最近的那个聚点
2、统计所有同类点的中点,将聚点移到这个中点
重复1.2两个过程直到中心点不再变化,为了稳健可以多次算法选取最优的分类
大概过程如图所示:
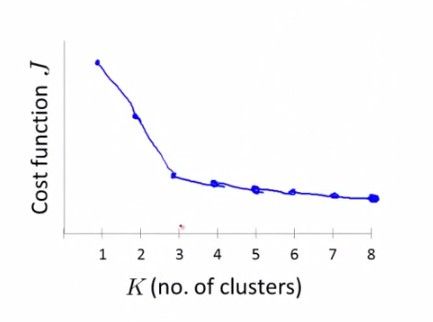
一些值得注意的细节是,初始化的时候可以随机从样例中选择k个点作为初始聚点(k是据点数),k值的选取最好是人工选取,另一种兼容性较差的方法就是测试k值找到拐点(elbow):下图拐点为3.
(以上内容来自我的coursera学习笔记8)下面将是本堂课补充的关于K-Means的内容
/////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////可以定义误差:distortion function
迭代过程也就是J减少的过程,但是J不是凸函数,所以不能保证收敛到global minimum,所以给出一个J,可能会有不同的聚类方式。
所以最好多次聚类选择最好的结果
///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
接下来提到了Anomaly Detection,这在coursera上也有提到,同样参看coursera学习笔记8
由此引出了Mixture of Gaussians得概念:数据由多个高斯分布混合而成。
通过最大似然可以求出三个参数的值
其中z(i)是指第i的样本被分为第多少个高斯分布。z(i)=j 也就是说第i个点被分为是由第j个高斯分布产生的点
这是在知道z(i)的情况下,事实上我们不知道,所以可以通过猜测-》修正-》猜测的迭代来求出最佳的z(i)
这就是EM(高斯分布的一个特例,再下面会介绍更加一般的EM算法)算法的思路
其中的w其实就是z,相对z来说要“软”一些,z可以看作对特定组为1,其他为0的w参数。
w表示的是每个点分到每类的概率。
////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
一般的EM算法
给一个定义:Jensen's inequality:对后面的推导有用
这是f为严格的凸函数的时候的不等式,而如果f为凹函数,不等式反向即可。
当X为常数时等号成立
//////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////
下面是推导过程
这个问题的最大似然函数是:
通过进一步推导可以得到如下结果
Q(z(i))可以看作是那个分式的概率密度,则第二个∑的部分可以看作分式的期望
又因为log函数是一个凹函数,借用上面的Jensen's inequality,可以得到
最大似然函数就有了一个下界,而EM算法就是通过每次确定下界,找到相对此下界更优的一个位置再作为下界
最后会得到一个局部最优的值。也就是说一次次放大下界值,最后converge到局部最优值
所以我们要让不等式相等,通过上面我们知道不等式相等只有当E[]中得数为常数时才会相等,而且Q(z(i))的和为1
可以得到:
所以可以得到EM算法的过程:
整个过程大概就是通过数次调整下界最后得到最大似然值