动态规划求最小代价矩阵链相乘
/*
在2014.3.20进行修改
修改内容1:
主要是改版下,以前的格式在某次CSDN抽风后,都没了,本来应该格式很好看的。
修改内容2:
竟然出bug了,在MATRIX_CHAIN_ORDER()中的:
for(int k=i;k<j;k++)
{
int q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(q<m[i][j])
{
m[i][j]=q;
s[i][j]=k;
}
被我写成了:
for(int k=i;k<=j;k++)
{
int q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(q<m[i][j])
{
m[i][j]=q;
s[i][j]=k;
}
竟然没人发现,我好失败啊。。
*/
矩阵相乘:
for i -> m for j -> p C[i,j] = 0 for k -> n C[i,j] += A[i,k] * B[k,j]
MATRIX_MULTIPLY (A,B) if columns[A] != rows[B] then error "incompatible dimensions" else for i = 1 to rows[A] for j = 1 to columns[B] C[i,j] = 0 for k = 1 to columns[A] C[i,j] = C[i,j]+A[i,k]*B[k,j] return C
稍微用C++实现了下就是:
/*Ouyang code for test MATRIX_MULTIPLY*/
#include <iostream>
#include "stdio.h"
#define N 4
using namespace std;
void Matrix_Multiply(int A[][N],int B[][N])
{
int C[N][N];
for(int i=0;i<N;i++)
for(int j=0;j<N;j++)
{
C[i][j]=0;
for(int k=0;k<N;k++)
{
C[i][j]+=A[i][k]*B[k][j];
}
}
for(int i=0;i<N;i++)
{
for(int j=0;j<N;j++)
{
printf("%d\t",C[i][j]);
}
printf("\n");
}
}
int main()
{
int A[4][4]={1,1,1,1,
1,1,1,1,
1,1,1,1,
1,1,1,1};
int B[4][4]={1,1,1,1,
1,1,1,1,
1,1,1,1,
1,1,1,1};
Matrix_Multiply(A,B);
return 0;
}
/*code end*/
时间开销
从上面的算法看出,每次矩阵相乘,就是一个三循环。
对于 A[M,N] 和 B[N,P] ,时间开销就是 MNP
多矩阵相乘的顺序决定了时间开销大小
A[10][100] B[100][5] C[5][50] 三个矩阵相乘
如果是(AB)C 则是10*100*5 + 10*5*50== 5000 + 2500 =7500
如果是A(BC) 则是100*5*50 + 10*100*50== 25000 + 50000 =75000
时间开销相差了 10 倍!
于是就有了这个课题:最小代码矩阵链相乘!
动态规划第一步:最优子结构
所以矩阵链AiAi+1...Aj的最优加全部括号为(AiAi+1...Ak)*(Ak+1Ak+2...Aj)
其中(AiAi+1...Ak),(Ak+1Ak+2...Aj)也是最优加全部括号,
可用反证法证明之:
如果它们不是最优的,那么存在一个最优的让它们相乘后的矩阵链是比最优的还最优,矛盾。
动态规划第二步:求一个递归解
m[i,j]就等于计算子乘积Ai..k以及Ak+1..j各自的代价加上两者相乘后的代价:pi-1pkpj。
此时我们并不知道k为何值,但是知道k在i...j之间。
m[i,j] = {
0, i == j;
min{m[i,k]+m[k+1,j]+pi-1pkpj} ,i<j;
}
动态规划第三步:计算最优代价
假设矩阵Ai的维数是pi-1*pi,i=1,2,3,...n.输入一个序列p={p0,p1,p2,p3...pn},其中length[p] == n+1.
使用一个辅助表m[1..n,1..n]来保存m[i,j]的代价
使用辅助表s[1..n,1..n]来记录计算m[i,j]取得最优代价处k的值。
我们将利用表格s来构造一个最优解。
MATRIX_CHAIN_ORDER(p) n = length[p]-1 for i = 1 to n //初始化代价表 m[i,i] = 0 //因为长度为1的链不需计算,最小代价为0 for l = 2 to n //l为链的长度,从链长度为2一直到n,算完n就得到结果了 for i = 1 to n-l+1 j = i+l-1 m[i,j] = 正无穷 for k = i to j-1 q = m[i,k]+m[k+1,j]+pi-1pkpj; if q < m[i,j] //不是最小,替换 m[i,j] = q s[i,j] = k return m,s
这么理解,依次:
链长度为2的各个最优状态
链长度为3的各个最优状态
链长度为4的各个最优状态
链长度为5的各个最优状态
...
链长度为n的各个最优状态
当前的状态被之前的状态所决定。
简单的C++大概是这样:
/*ouyang's code*/
void MATRIX_CHAIN_ORDER(int p[])
{
int n=length;
int m[length][length];
int s[length][length];
for(int i=1;i<=n;i++) //长度为1的链代价是0
{
m[i][i]=0;
}
for(int l=2;l<=n;l++) //自底向上m[i,j]增长,l为链的长度,逐步增长
{
for(int i=1;i<=n-l+1;i++)
{
int j=i+l-1;
m[i][j]=MAX;
for(int k=i;k<j;k++)
{
int q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(q<m[i][j])
{
m[i][j]=q; //记录最小代价的m
s[i][j]=k; //记录最小代价时的k
}
}
}
}
}
/*code end*/
动态规划第四步:构造一个最优解
PRINT_OPTIMAL_PARENS(s,i,j)
if i == j
print "A"+i
else
print "("
PRINT_OPTIMAL_PARENS(s,i,s[i,j]);
PRINT_OPTIMAL_PARENS(s,s[i,j]+1,j);
print ")"
简单的C++代码:
/*ouyang's code*/
void PRINT_OPTIMAL_PARENS(int s[][length+1],int i,int j)
{
if (i == j)
{
printf("A%d",i);
}
else
{
printf("(");
PRINT_OPTIMAL_PARENS(s,i,s[i][j]);
PRINT_OPTIMAL_PARENS(s,s[i][j]+1,j);
printf (")");
}
}
/*code end*/
全部代码
/*ouyang's all code */
#include <iostream>
#include "stdio.h"
#define N 4
#define length 6
#define MAX 65000
using namespace std;
int s[length+1][length+1];
void MATRIX_CHAIN_ORDER(int p[])
{
int n=length;
int m[length+1][length+1];
for(int i=1;i<=n;i++)
{
m[i][i]=0;
}
for(int l=2;l<=n;l++)
{
for(int i=1;i<=n-l+1;i++)
{
int j=i+l-1;
m[i][j]=MAX;
for(int k=i;k<j;k++)
{
int q=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if(q<m[i][j])
{
m[i][j]=q;
s[i][j]=k;
}
}
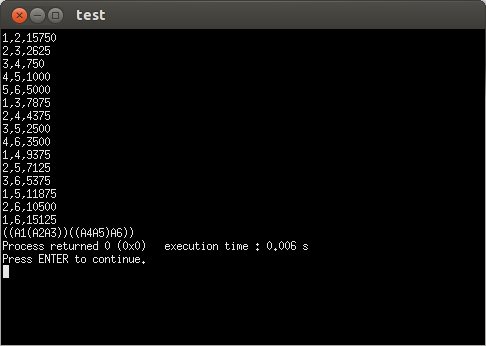
cout<<i<<","<<j<<","<<m[i][j]<<endl;
}
}
}
void PRINT_OPTIMAL_PARENS(int s[][length+1],int i,int j)
{
//递归调用,打印矩阵加全部括号的顺序
if (i == j)
{
printf("A%d",i);
}
else
{
printf("(");
PRINT_OPTIMAL_PARENS(s,i,s[i][j]);
PRINT_OPTIMAL_PARENS(s,s[i][j]+1,j);
printf (")");
}
}
int main()
{
/*这个程序是为了得到最小代价的矩阵链乘法,所以结果只是得到怎么去相乘矩阵
而没有去计算矩阵相乘最后的矩阵。
*/
int p[length+1]={30,35,15,5,10,20,25};
MATRIX_CHAIN_ORDER(p);
PRINT_OPTIMAL_PARENS(s,1,6);
return 0;
}
/*code end*/