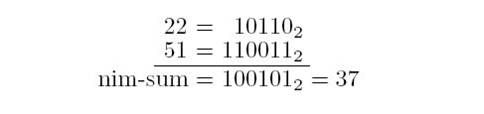MiYu原创, 转帖请注明 : 转载自 ______________白白の屋
寻找平衡状态(也称必败态, 奇异局势),(满足:任意非平衡态经过一次操作可以变为平衡态)
(一)巴什博奕(Bash Game):
只有一堆n个物品,两个人轮流从这堆物品中取物,规定每次至少取一个,最多取m个.最后取光者得胜.
n = (m+1)r+s , (r为任意自然数,s≤m), 即n%(m+1) != 0, 则先取者肯定获胜
(二)威佐夫博奕(Wythoff Game):
有两堆各若干个物品,两个人轮流从某一堆或同时从两堆中取同样多的物品,规定每次至少取一个,多者不限,最后取光者得胜.
(ak,bk)(ak ≤ bk ,k=0,1,2,...,n)表示奇异局势
求法:
ak =[k(1+√5)/2], bk= ak + k (k=0,1,2,...,n 方括号表示取整函数)
判断:
Gold=(1+sqrt(5.0))/2.0;
1)假设(a,b)为第k种奇异局势(k=0,1,2...) 那么k=b-a;
2)判断其a==(int)(k*Gold),相等则为奇异局势
(注:采用适当的方法,可以将非奇异局势变为奇异局势.
假设面对的局势是(a,b)
若 b = a,则同时从两堆中取走 a 个物体,就变为了奇异局势(0,0);
1. 如果a = ak,
1.1 b > bk, 那么,取走b - bk个物体,即变为奇异局势(ak, bk);
1.2 b < bk 则同时从两堆中拿走 ak – a[b – ak]个物体,变为奇异局势( a[b – ak] , a[b – ak]+ b - ak);
2 如果a = bk ,
2.1 b > ak ,则从第二堆中拿走多余的数量b – ak
2.2 b < ak ,则 若b = aj (j < k) 从第一堆中拿走多余的数量a– bj; (a > bj)
若b = bj (j < k) 从第一堆中拿走多余的数量a– aj; ( a > aj)
)
例题:pku 1067
(三)尼姆博奕(Nimm Game):
有n堆各若干个物品,两个人轮流从某一堆取任意多的物品,规定每次至少取一个,多者不限,最后取光者得胜.
任何奇异局势(a1, a2, … , an)都有a1(+)a2(+)…(+)an =0. ( (+)为 按位^)
Nim游戏简介:
(1)有两个玩家;
(2)有三堆扑克牌(比如:可以分别是5,7,9张);
游戏双方轮流操作;
(3)玩家的每次操作是选择其中某一堆牌,然后从中取走任意张;
最后一次去拍的一方为获胜方;
定义: 假设 (xm · · · x0)2 和(ym · · · y0)2 的nim-sum是(zm · · · z0)2,则我们表示成 (xm · · · x0)2 ⊕ (ym · · · y0)2 = (zm · · · z0)2,
这里,zk = xk + yk (mod 2)(k=0…m).
nim游戏的定理一:
对于nim游戏的某个位置(x1,x2,x3),当且仅当它各部分的nim-sum等于0时(即x1⊕x2⊕x3=0)(x1,x2,x3做异或操作^),则当前位于必败点。
定理一也适用于更多堆的情况!
例题:pku 2234
例题:hdu 1730
例题:pku 1740
例题:pku 1704
例题:pku 1082 (大量分析… 结论很简单。 也可以根据简单的推论模拟实现。)