POJ 1985 Cow Marathon & HDU 2196 Computer 【简单树形dp - 树的直径】
我蒟蒻啊,对于树形dp的理解还很浅显,先把初步的几道题理解记录一下。dp要找最优子结构,它的状态转移就要有一个序。树上的dp同样,无非是按照树的生长方向或逆方向进行dp。对于所谓根-叶,叶-根,这两个概念还没有特别明确的认识。单就这两道题而言,无非是某节点到其所有后继节点的状态转移。
poj1985 是 求 树的直径。可以随便选择一个点开始进行bfs或者dfs,从而找到离该点最远的那个点(可以证明,离树上任意一点最远的点一定是树的某条直径的两端点之一;树的直径:树上的最长简单路径)。再从找到的点出发,找到据该点的最远点,那么这两点就确定了树的一条直径,两点间距即为所求距离。
hdu2196利用的是上段括号内的性质,既然要找出到树上每一点的最远距离,那么只要找出树的直径的两个端点即可,从这两点出发遍历树,确定分别到这两点的距离,距离大者所求。
自觉这两题都是按照搜索过的。但是应该思考其中的dp原理。因为树的性质保证了搜索策略的无后效性(已达点不会再次访问,所以第一次到达的时候的距离即为真实距离);而每一步记录距离值的做法,仿佛又体现了(备忘录)记忆化搜的特点,新点距离完全基于上一点距离,而且上一点距离当搜过之后便已记录下来。
再次重申,记忆化搜无非就是爆搜+记录状态。没有很死板的条条框框,什么搜到不能再搜为止才可以开始记录。因为,只要确认你开始搜或者结束搜的某一点是末状态,即无再可转移之状态之后,大可以开始记录。一路前推或者后推过去,就得了所有的正确状态。
暂记于此,勉励自己,继续树上dp!!关键点:运用树的性质!
链接: http://poj.org/problem?id=1985
Cow Marathon
| Time Limit: 2000MS | Memory Limit: 30000K | |
| Total Submissions: 2054 | Accepted: 950 | |
| Case Time Limit: 1000MS | ||
Description
After hearing about the epidemic of obesity in the USA, Farmer John wants his cows to get more exercise, so he has committed to create a bovine marathon for his cows to run. The marathon route will include a pair of farms and a path comprised of a sequence of roads between them. Since FJ wants the cows to get as much exercise as possible he wants to find the two farms on his map that are the farthest apart from each other (distance being measured in terms of total length of road on the path between the two farms). Help him determine the distances between this farthest pair of farms.
Input
* Lines 1.....: Same input format as "Navigation Nightmare".
Output
* Line 1: An integer giving the distance between the farthest pair of farms.
Sample Input
7 6 1 6 13 E 6 3 9 E 3 5 7 S 4 1 3 N 2 4 20 W 4 7 2 S
Sample Output
52
Hint
The longest marathon runs from farm 2 via roads 4, 1, 6 and 3 to farm 5 and is of length 20+3+13+9+7=52.
Source
USACO 2004 February
/*
Coded by BUPT-[aswmtjdsj] @ Penalty in 915
*/
/*
tree's diameter
BFS twice
first to find one of the end point (from arbitrary point)
then find the other end point(the farthest point from the initial end point)
*/
#include < queue >
#include < iostream >
#include < cstdio >
using namespace std;
#define maxn 40002
#include < cstring >
struct edge
{
int p,next,w;
edge(){}
edge( int a, int b, int c):p(a),next(b),w(c){}
}v[maxn],e[maxn * 2 ];
int n,m,tot;
int d[maxn];
void init()
{
tot = 0 ;
for ( int i = 1 ;i <= n;i ++ )
v[i].next = - 1 ;
}
void add( int p, int q, int w)
{
e[tot] = edge(q,v[p].next,w);
v[p].next = tot ++ ;
}
void adde( int p, int q, int w)
{
add(p,q,w);
add(q,p,w);
}
const int inf = 1 << 30 ;
int bfs( int x)
{
for ( int i = 1 ;i <= n;i ++ )
d[i] = inf;
d[x] = 0 ;
queue < int > Q;
Q.push(x);
while ( ! Q.empty())
{
int now = Q.front();
Q.pop();
for ( int k = v[now].next; ~ k;k = e[k].next)
{
if (d[e[k].p] > d[now] + e[k].w)
{
d[e[k].p] = d[now] + e[k].w;
Q.push(e[k].p);
}
}
}
int mark = 0 ,MM = 0 ;
for ( int i = 1 ;i <= n;i ++ )
{
if (MM < d[i])
{
MM = d[i];
mark = i;
}
}
return mark;
}
int main()
{
while (scanf( " %d %d " , & n, & m) == 2 )
{
init();
for ( int i = 0 ;i < m;i ++ )
{
int a,b,c;
char dd;
scanf( " %d %d %d %c " , & a, & b, & c, & dd);
adde(a,b,c);
}
int mark = bfs( 1 );
int ans = bfs(mark);
printf( " %d\n " ,d[ans]);
}
}
Coded by BUPT-[aswmtjdsj] @ Penalty in 915
*/
/*
tree's diameter
BFS twice
first to find one of the end point (from arbitrary point)
then find the other end point(the farthest point from the initial end point)
*/
#include < queue >
#include < iostream >
#include < cstdio >
using namespace std;
#define maxn 40002
#include < cstring >
struct edge
{
int p,next,w;
edge(){}
edge( int a, int b, int c):p(a),next(b),w(c){}
}v[maxn],e[maxn * 2 ];
int n,m,tot;
int d[maxn];
void init()
{
tot = 0 ;
for ( int i = 1 ;i <= n;i ++ )
v[i].next = - 1 ;
}
void add( int p, int q, int w)
{
e[tot] = edge(q,v[p].next,w);
v[p].next = tot ++ ;
}
void adde( int p, int q, int w)
{
add(p,q,w);
add(q,p,w);
}
const int inf = 1 << 30 ;
int bfs( int x)
{
for ( int i = 1 ;i <= n;i ++ )
d[i] = inf;
d[x] = 0 ;
queue < int > Q;
Q.push(x);
while ( ! Q.empty())
{
int now = Q.front();
Q.pop();
for ( int k = v[now].next; ~ k;k = e[k].next)
{
if (d[e[k].p] > d[now] + e[k].w)
{
d[e[k].p] = d[now] + e[k].w;
Q.push(e[k].p);
}
}
}
int mark = 0 ,MM = 0 ;
for ( int i = 1 ;i <= n;i ++ )
{
if (MM < d[i])
{
MM = d[i];
mark = i;
}
}
return mark;
}
int main()
{
while (scanf( " %d %d " , & n, & m) == 2 )
{
init();
for ( int i = 0 ;i < m;i ++ )
{
int a,b,c;
char dd;
scanf( " %d %d %d %c " , & a, & b, & c, & dd);
adde(a,b,c);
}
int mark = bfs( 1 );
int ans = bfs(mark);
printf( " %d\n " ,d[ans]);
}
}
Computer
Time Limit: 1000/1000 MS (Java/Others) Memory Limit: 32768/32768 K (Java/Others)
Total Submission(s): 347 Accepted Submission(s): 162
Problem Description
A school bought the first computer some time ago(so this computer's id is 1). During the recent years the school bought N-1 new computers. Each new computer was connected to one of settled earlier. Managers of school are anxious about slow functioning of the net and want to know the maximum distance Si for which i-th computer needs to send signal (i.e. length of cable to the most distant computer). You need to provide this information.
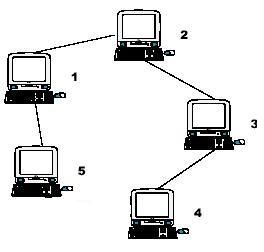
Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.

Hint: the example input is corresponding to this graph. And from the graph, you can see that the computer 4 is farthest one from 1, so S1 = 3. Computer 4 and 5 are the farthest ones from 2, so S2 = 2. Computer 5 is the farthest one from 3, so S3 = 3. we also get S4 = 4, S5 = 4.
Input
Input file contains multiple test cases.In each case there is natural number N (N<=10000) in the first line, followed by (N-1) lines with descriptions of computers. i-th line contains two natural numbers - number of computer, to which i-th computer is connected and length of cable used for connection. Total length of cable does not exceed 10^9. Numbers in lines of input are separated by a space.
Output
For each case output N lines. i-th line must contain number Si for i-th computer (1<=i<=N).
Sample Input
5 1 1 2 1 3 1 1 1
Sample Output
3 2 3 4 4
Author
scnu
/*
Coded by BUPT-[aswmtjdsj] @ Penalty in 608
*/
/*
from an arbitrary point to find the farthest point (it must be an endpoint of the tree's diameter
from the new point dfs to find every d[i] and the other end point of the diameter
then from this point dfs again to find every p[i]
print (d[i] > p[i])?d[i] : p[i]
because the farthest point from arbitrary point is either one end point of the diameter or the other .
.
easily to yy
a problem of tree dp or we say dfs search .
.
*/
#include < iostream >
#include < cstdio >
#include < cstring >
#include < cctype >
#include < string >
#include < sstream >
#include < fstream >
#include < algorithm >
#include < vector >
#include < bitset >
#include < ctime >
#include < cstdlib >
#include < map >
#include < set >
#include < cmath >
#include < queue >
#define see(x) cerr << " LINE " << __LINE__ << ":" << #x << " : " << x << endl
#define SP system("pause")
using namespace std;
const double pi = acos( - 1.0 );
const double eps = 1e - 8 ;
const int inf = 100000005 ;
const int dx[ 4 ] = { 0 , 0 , - 1 , 1 };
const int dy[ 4 ] = { - 1 , 1 , 0 , 0 };
#define left(x) ((x) << 1)
#define right(x) (((x) << 1) + 1)
#define parent(x) ((x) >> 1)
#define maxn 10005
#define maxe (maxv * maxv)
#define sqr(x) ((x) * (x))
#define PQ priority_queue
#define PB push_back
struct edge
{
int p,next,w;
edge(){}
edge( int a, int b, int c):p(a),next(b),w(c){}
}v[maxn],e[maxn * 2 ];
int n,tot;
void init()
{
tot = 0 ;
for ( int i = 1 ;i <= n;i ++ )
v[i].next = - 1 ;
}
void add( int p, int q, int c)
{
e[tot] = edge(q,v[p].next,c);
v[p].next = tot ++ ;
}
int d[maxn],p[maxn];
void dfs( int x)
{
for ( int k = v[x].next; ~ k;k = e[k].next)
if (d[e[k].p] == inf)
{
d[e[k].p] = d[x] + e[k].w;
dfs(e[k].p);
}
}
void dfs1( int x)
{
for ( int k = v[x].next; ~ k;k = e[k].next)
if (p[e[k].p] == inf)
{
p[e[k].p] = p[x] + e[k].w;
dfs1(e[k].p);
}
}
int main()
{
while (scanf( " %d " , & n) == 1 )
{
init();
for ( int i = 2 ;i <= n;i ++ )
{
int a,b;
scanf( " %d %d " , & a, & b);
add(i,a,b);
// printf("%d %d %d",i,a,b);
add(a,i,b);
}
for ( int i = 1 ;i <= n;i ++ )
d[i] = inf;
d[ 1 ] = 0 ;
dfs( 1 );
/* for(int i = 1;i <= n;i++)
printf("%d\n",d[i]); */
int maxx = 0 ,mark = 1 ;
for ( int i = 1 ;i <= n;i ++ )
{
if (d[i] > maxx)
{
maxx = d[i];
mark = i;
}
}
for ( int i = 1 ;i <= n;i ++ )
d[i] = inf;
d[mark] = 0 ;
dfs(mark);
maxx = 0 ,mark = 1 ;
for ( int i = 1 ;i <= n;i ++ )
{
if (d[i] > maxx)
{
maxx = d[i];
mark = i;
}
}
for ( int i = 1 ;i <= n;i ++ )
p[i] = inf;
p[mark] = 0 ;
dfs1(mark);
for ( int i = 1 ;i <= n;i ++ )
printf( " %d\n " ,(d[i] > p[i]) ? d[i] : p[i]);
}
}
Coded by BUPT-[aswmtjdsj] @ Penalty in 608
*/
/*
from an arbitrary point to find the farthest point (it must be an endpoint of the tree's diameter
from the new point dfs to find every d[i] and the other end point of the diameter
then from this point dfs again to find every p[i]
print (d[i] > p[i])?d[i] : p[i]
because the farthest point from arbitrary point is either one end point of the diameter or the other
easily to yy
a problem of tree dp or we say dfs search
*/
#include < iostream >
#include < cstdio >
#include < cstring >
#include < cctype >
#include < string >
#include < sstream >
#include < fstream >
#include < algorithm >
#include < vector >
#include < bitset >
#include < ctime >
#include < cstdlib >
#include < map >
#include < set >
#include < cmath >
#include < queue >
#define see(x) cerr << " LINE " << __LINE__ << ":" << #x << " : " << x << endl
#define SP system("pause")
using namespace std;
const double pi = acos( - 1.0 );
const double eps = 1e - 8 ;
const int inf = 100000005 ;
const int dx[ 4 ] = { 0 , 0 , - 1 , 1 };
const int dy[ 4 ] = { - 1 , 1 , 0 , 0 };
#define left(x) ((x) << 1)
#define right(x) (((x) << 1) + 1)
#define parent(x) ((x) >> 1)
#define maxn 10005
#define maxe (maxv * maxv)
#define sqr(x) ((x) * (x))
#define PQ priority_queue
#define PB push_back
struct edge
{
int p,next,w;
edge(){}
edge( int a, int b, int c):p(a),next(b),w(c){}
}v[maxn],e[maxn * 2 ];
int n,tot;
void init()
{
tot = 0 ;
for ( int i = 1 ;i <= n;i ++ )
v[i].next = - 1 ;
}
void add( int p, int q, int c)
{
e[tot] = edge(q,v[p].next,c);
v[p].next = tot ++ ;
}
int d[maxn],p[maxn];
void dfs( int x)
{
for ( int k = v[x].next; ~ k;k = e[k].next)
if (d[e[k].p] == inf)
{
d[e[k].p] = d[x] + e[k].w;
dfs(e[k].p);
}
}
void dfs1( int x)
{
for ( int k = v[x].next; ~ k;k = e[k].next)
if (p[e[k].p] == inf)
{
p[e[k].p] = p[x] + e[k].w;
dfs1(e[k].p);
}
}
int main()
{
while (scanf( " %d " , & n) == 1 )
{
init();
for ( int i = 2 ;i <= n;i ++ )
{
int a,b;
scanf( " %d %d " , & a, & b);
add(i,a,b);
// printf("%d %d %d",i,a,b);
add(a,i,b);
}
for ( int i = 1 ;i <= n;i ++ )
d[i] = inf;
d[ 1 ] = 0 ;
dfs( 1 );
/* for(int i = 1;i <= n;i++)
printf("%d\n",d[i]); */
int maxx = 0 ,mark = 1 ;
for ( int i = 1 ;i <= n;i ++ )
{
if (d[i] > maxx)
{
maxx = d[i];
mark = i;
}
}
for ( int i = 1 ;i <= n;i ++ )
d[i] = inf;
d[mark] = 0 ;
dfs(mark);
maxx = 0 ,mark = 1 ;
for ( int i = 1 ;i <= n;i ++ )
{
if (d[i] > maxx)
{
maxx = d[i];
mark = i;
}
}
for ( int i = 1 ;i <= n;i ++ )
p[i] = inf;
p[mark] = 0 ;
dfs1(mark);
for ( int i = 1 ;i <= n;i ++ )
printf( " %d\n " ,(d[i] > p[i]) ? d[i] : p[i]);
}
}