POJ 1813 哈希表算法

题目地址： http://poj.org/problem?id=2002

题目的大意是在二维平面上有很多点，问有多少种可能组成正方形。假设这些点的坐标都可以用int来表示

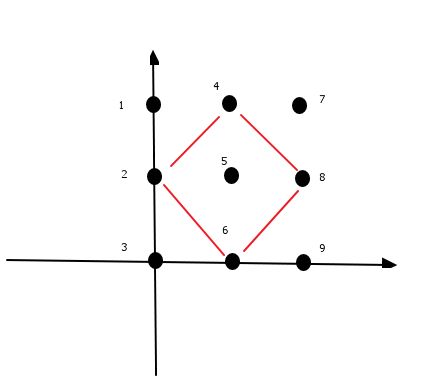
例如下面图是一个例子： 

可以形成的正方形是6个，有一个比较特殊的红色的正方形。

这个题目如果用暴力所有的话，显然是4层循环，看选中的四个点能否构成正方形。不过显然这么高的复杂度，一定会超时的。

下面的做法是我在discussion里看到的，如果自己设计还真的设计不出来，本文加上了一些自己的理解和想法。

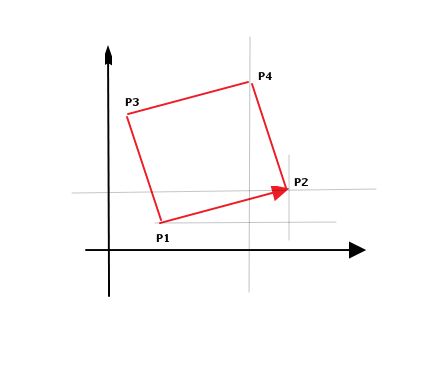
我们可以这样想，对于任意两个点（P1 P2), 假设是一个向量，方向是P1P2，我们可以求出这个向量一侧的两个点P3P4，P1P2P3P4正好构成正方形。

例如图所示

在这个图中，利用三角形相等的条件，我们可以知道对于P2P4，它在x上的变化正好P1P2在y上的变化，P2P4在y上的变化正好等于P1P2在X上的变化。对于P3也可以得出类似的结论。

所以

P[3].x=P[1].x+(P[1].y-P[2].y);
P[3].y=P[1].y+(P[2].x-P[1].x);

P[4].x=P[2].x+(P[1].y-P[2].y);
P[4].y=P[2].y+(P[2].x-P[1].x);

下一步就是哈希的魅力所在了，求出这两个点，然后再哈希里检索，如果在哈希表里，则将ans + 1。否则跳过。

不过我们会发现一个问题，对于同一个正方形P1P2P4P3, 我们在判断的时候，查找到P1P2, 总结果数ans+1， 对于P2P4, ans+1， 对于P4P3 ans +1, 对于P3P1 ans+1。

所以这样最后的结果要 /4。这样程序的总效率从O(n^4)降低到O(n^2)

代码如下: 

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <algorithm>

using namespace std;
#define MAX_NUM 20000
#define PRIME 19977

struct Point
{
	int x;
	int y;
};

bool cmp(const Point& a,const Point &b)
{
	if(a.x==b.x)
		return a.y<b.y;
	return a.x<b.x;
}

int HashTable[PRIME];
Point  data[1005];
int nPoint;

int GetHashCode(const Point& p)
{
	return (abs(p.x) * 50 + abs(p.y)) % PRIME; //这里要保证hashcode是正数，我在这里RE好几次
}

void InsertIntoHash(int i)//插入哈希表
{
	int hashCode = GetHashCode(data[i]);

	if(HashTable[hashCode] == -1)
	{
		HashTable[hashCode] = i;
	}
	else
	{
		int t = (hashCode + 1) % PRIME;
		while(HashTable[t] != -1)
		{
			t++;
			t %= PRIME;
		}
		HashTable[t] = i;
	}
}
bool PointEqual(const Point &p1,const Point &p2)
{
	return p1.x == p2.x && p1.y == p2.y;
}
bool SearchInhashTable(const Point &point)//在哈希表里查找
{
	int hashCode = GetHashCode(point);

	if(HashTable[hashCode] == -1)
	{
		return false;
	}
	else
	{
		int t = hashCode;
		while(HashTable[t] != -1 && !PointEqual(point, data[HashTable[t]]) )
		{
			t++;
			t %= PRIME;
		}
		if(HashTable[t] == -1)
		{
			return false;
		}
		return true;
	}
}


int main()
{
	int x,y;
	while(scanf("%d", &nPoint) && nPoint)
	{
		memset(HashTable, -1, sizeof(HashTable));
		for( int i = 0; i < nPoint; i++) 
		{
			scanf("%d%d", &data[i].x, &data[i].y);
		}
		//sort(data, data + nPoint, cmp);//下面改进后修改的代码
		for(int i = 0; i < nPoint; i++)
		{
			InsertIntoHash(i);
		}

		int sum = 0;

		Point tmp;
		int ans = 0;
		for( int i = 0; i < nPoint; i++)
		{
			for( int j = 0; j < nPoint; j++)//改进后修改为 j = i + 1
			{
				if( i != j)
				{

					x=data[i].x+data[i].y-data[j].y;
					y=data[i].y+data[j].x-data[i].x;
					tmp.x = x;
					tmp.y = y;
					if(!SearchInhashTable(tmp))
						continue;
					x=data[j].x+data[i].y-data[j].y;
					y=data[j].y+data[j].x-data[i].x;
					tmp.x = x;
					tmp.y = y;
					if(SearchInhashTable(tmp))
						ans++;
				}

			
			}
		}
		printf("%d\n", ans/4);
	}
	return 0;
}

当然算法其实还是有加速的余地，至少可以提高将近2倍的效率。因为我们发现在我们的测试数据中P1P2会测试，P2P1也会测试，并且这样的测试是没有意义的（因为P4P3会做等效的测试）

所以我们可以把内侧的循环，改成 j = i+1

不过这里还有一个问题，如果原始序列中点的排序是 P1 P2 P4 P3, 那样的话，我们在测试P1P2后，等效测试是P4P3, 这样就没有测试过P3P4这种本应做测试的情况。

那么如何改进呢，答案是将所有的点排序，按照x优先，然后y的次序将点排序。

这样遍历点的时候，可以保证两组测试都是不会重复的。