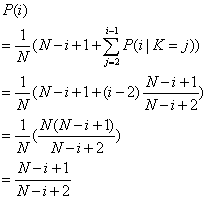【算法与数据结构】金刚坐飞机问题
文章背景
编程之美 4.1 “金刚坐飞机问题”的问题2,难度比问题1大很多。
编程之美的官方解法,包括原理分析、概率公式、推导过程等,感觉阐述不够详细,没有完全读懂。
搜索一下 “金刚坐飞机”,参考了几个很不错的分析,得到一个自己觉得比较完整的答案。
仔细审题
首先,仔细审题,有两个细节需要搞清楚:
- 飞机上总共有多少座位?N?N+1?还是更多?从问题1的官方解答看,飞机上座位总数为N。
- “...乘客们正准备按机票编号(1,2,3...N)依次排队登机。突然来了一只大猩猩(对,他叫金刚)。他也有飞机票,但是...”,金刚的机票编号是否属于闭区间[1,N]?换句话说,所有乘客(包括金刚)的总数是N还是N+1?既然座位总数为N,金刚也有飞机票,飞机也不可能超载,因此,所有乘客(包括金刚)的总数为N。金刚的机票编号也属于闭区间[1,N]。
推敲官方答案
然后,看一下编程之美的官方答案:第i个乘客坐在自己位置上的概率为 ![]() 。
。
既然飞机座位总数为N,根据官方答案,第1个乘客的概率为![]() 。实际上,第1个乘客的概率应该为
。实际上,第1个乘客的概率应该为![]() 。计算过程如下:
。计算过程如下:
根据全概率公式,第1个乘客坐在自己座位上的概率:

如何解释这个问题呢?从问题2的官方解答过程“如果n=1或n>i,那么第i个乘客坐在自己位置上的概率为1....”可以推测,官方认为金刚的机票编号为1。官方答案中的i应该不包括1。
重新描述问题
到这里,我重新描述一下问题:
飞机上有N个座位,座位编号依次为1,2,..N。恰好有N个乘客排队登机,第1个乘客的座位编号是1,第2个乘客的座位编号是2,...,第N个乘客的座位编号是N。每个乘客都应该坐在编号正确的座位上。但是,第1个乘客是不讲道理的金刚,他第一个进入飞机,随便(随机)挑了一个座位坐下。其他乘客敢怒不敢言,只好依次找座位坐下。如果自己的座位没有被占,则坐自己的作为,否则,也像金刚那样随便挑一个座位。现在,求第i个乘客(第1个乘客还是金刚)坐到自己座位的概率是多少?
我算出的答案为:
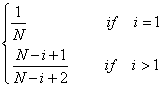
与官方答案是一致的,但是本文会给出更加详细的计算过程。
概率计算过程
先计算金刚的概率
再计算其他乘客的概率
核心工具是全概率公式
- P(K=j)表示,金刚坐在座位j的概率
- P(i|K=j)表示,在金刚坐在座位j上的情况下,第i个乘客坐在座位i的概率
- 如果j=1,也就是说金刚居然坐在了自己的座位上,第i个乘客(其实是所有其他乘客)必然能够坐到自己座位,因此P(K=j) = 1。
- 如果j=i,也就是说金刚居然坐在了第i个乘客的座位上,第i个乘客肯定不能坐到自己座位,因此P(K=j) = 0。
- 如果j>i,也就是说,金刚坐了(第i个乘客)后面的座位,不影响前面乘客找座位,第i个乘客(其实是第2~j-1个乘客)必然能够坐到自己座位,因此P(K=j) = 1。
- 如果1<j<i,也就是说,金刚抢了(第i个乘客)前面的座位,肯定会影响第i个乘客(其实是第j~N个乘客)的座位。
难点是计算条件概率
自顶向下计算条件概率
那么,1<j<i时,P(i|K=j)到底是怎么计算的呢?下面详细推导一下j=i-1和j=i-2这两种情况,其他情况可以顺推。
如果金刚坐在了座位i-1上,第i-1个乘客可以选择座位1、i、i+1~N。每种选择的概率均等,为1/(N-i+2):
- 如果第i-1个乘客选择座位1,则第i个乘客必然能坐到自己座位,概率为1
- 如果第i-1个乘客选择座位i,则第i个乘客必然不能坐到自己座位,概率为0
- 如果第i-1个乘客选择座位i+1~N,则第i个座位必然能坐到自己座位,概率为1
如果金刚坐在了座位i-2上,第i-2个乘客可以选择座位1、i-1、i~N。每种选择的概率均等,为1/(N-i+3):
- 如果第i-2个乘客选择座位1,则第i个乘客必然能坐到自己座位,概率为1
- 如果第i-2个乘客选择座位i-1,则第i-1个乘客的选择将影响第i个乘客的概率。此种情况恰好可以递归到P(i|K=i-1),只要假设第i-2个乘客就是金刚,它坐在了座位i-1上
- 如果第i-2个乘客选择座位i,则第i个乘客必然不能坐到自己座位,概率为0
- 如果第i-2个乘客选择座位i+1~N,则第i个座位必然能坐到自己座位,概率为1
挖掘递归现象
其实,从上述推导的过程中,我们已经发现递归的迹象,是否可以再深入挖掘一下递归公式,进而避免自顶向下的计算呢?
如果金刚坐在了座位j上,那么第j个乘客将会在座位1、j+1~N中随即选择一个座位。此时,乘客数量变成N-j+1,座位的数量也是N-j+1,第j个乘客恰好是剩余乘客的第1个,他变成了新的金刚。我们把他的座位编号从j换成1,这个变换不会影响问题的答案。下面我们来证明这个变换的安全性。
这个变换肯定会影响第j个乘客的概率,但是我们要计算的![]() 并不包括第j个乘客,所以不用考虑这个影响。对于第2~i-1个乘客而言,如果第j个乘客无论是坐在1还是j,他们都可以坐在自己的座位上,对他们来说没有区别,对他们的概率也没有任何影响。因此,这个变换是安全的。
并不包括第j个乘客,所以不用考虑这个影响。对于第2~i-1个乘客而言,如果第j个乘客无论是坐在1还是j,他们都可以坐在自己的座位上,对他们来说没有区别,对他们的概率也没有任何影响。因此,这个变换是安全的。
从问题的形式上看,变换之后的问题,与原问题等价,只是问题规模从N减小到N-j+1,且每位乘客的编号减小(j-1),座位编号也减小(j-1)。下面详细描述新问题:
飞机上有N-j+1个座位,座位编号依次为1,2,..N-j+1。恰好有N个乘客排队登机,第1个乘客的座位编号是1,第2个乘客的座位编号是2,...,第N-j+1个乘客的座位编号是N-j+1。每个乘客都应该坐在编号正确的座位上。但是,第1个乘客是不讲道理的金刚,他第一个进入飞机,随便(随机)挑了一个座位坐下。其他乘客敢怒不敢言,只好依次找座位坐下。如果自己的座位没有被占,则坐自己的作为,否则,也像金刚那样随便挑一个座位。现在,求第i个乘客(第1个乘客还是金刚)坐到自己座位的概率是多少?
利用递归形式计算条件概率
这里引入了一个新的变量n,表示乘客的总数。我们令F(i,n)表示在乘客总数为n的情况下,第i个乘客坐到自己座位的概率。显然,P(i) = F(i,N)。
下面,我们开始计算F(i,n),首先将P(i,N)计算结果中的N替换成n,然后利用子问题的递归形式。
结合金刚的概率,我们得到完整答案: