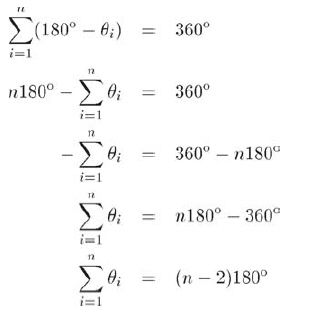3D几何图元(7)
一般来说,多边形是由顶点和边构成的平面物体。
简单多边形与复杂多边形
简单多边形不包含"洞",复杂多边形可能包含"洞"(图12.26)。简单多边形可以通过沿多边形列出的所有顶点来描述(左手坐标系中,通常以从多边形正面看时的顺时针方向列出所有点)。简单多边形的使用频率比复杂多边形高得多。
通过添加一对"接缝"边,能将任意复杂多边形转化成简单多边形,如图12.27所示。见右边的放大图,我们在每个"缝"添加了两个边,这两个边实际上是重合的,放大图中将其分开是为了让你看得更清楚。当我们考虑到绕多边形的边的顺序时,这两个接缝边的方向是相反的。
自相交多边形
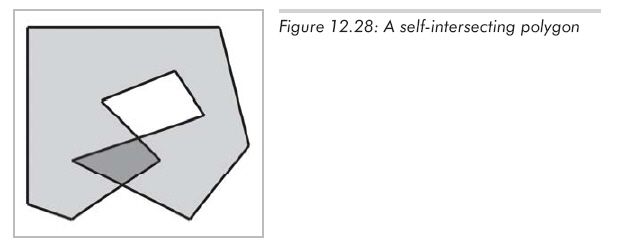
大多数简单多边形的边不相交,如果有的边相交了,那么这个多边形叫做自相交多边形。一个简单的自相交多边形如图12.28所示。
凸多边形与凹多边形
非自相交多边形能进一步细分为凸多边形和凹多边形。给凸多边形下一个精确定义是一件非常困难的事,因为存在很多令人棘手的退化形式。对大多数多边形,下列常用的定义是等价的。不过对于一些退化多边形来说,根据一种定义它是凸的,而根据另一种定义它又可能是凹的。
(1)直观上,凸多边形是没有任何"凹陷处"的,而凹多边形至少有一个顶点处于"凹陷处"----凹点。
(2)凸多边形,任意两顶点的连线都包含在多边形中。但在凹多边形中,总能找到一对顶点,它们的连线有一部分在多边形外。
(3)沿凸多边形周边移动时,在每个顶点的转向都是相同的。对凹多边形,一些是向右转,一些是向左转,在凹点的转向是相反的(注意这仅是对非自相交多边形来说的)。
前面曾提到过,退化多边形会使这些相对清晰的定义变得模糊不清。例如一些多边形有两个连续的顶点重合,或这一条边以相反的方向重复了两次。能认为这些多边形是凸的吗?实践中,经常用到下列凸性的定义:
(1)如果只能对凸多边形起作用的代码对这个多边形也能起作用,那么它就是凸的(也就是说如果一个定义没有被打破就不用修正它)。
(2)如果凸性测试算法判断它是凸的,那么它就是凸的(这是由"算法定义"解释的)。
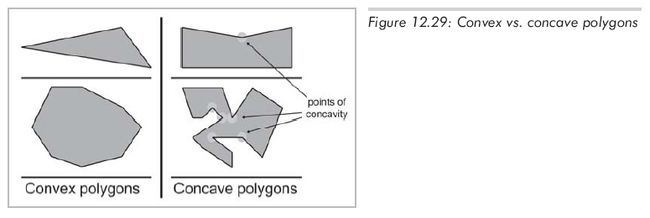
现在,让我们忽略一些病态情况,给出一些大家意见都一致的凸、凹多边形。如图12.29所示,右上角的凹多边形有1个凹点,而下面的凹多边形有5个凹点。
任意凹多边形都能分解为凸多边形片,它的基本思路是定位凹点并通过添加对角线来有系统地移除它们。
怎样才能知道一个多边形是凸的还是凹的?一种方法是检查各顶点的内角和,考虑n个顶点的凸多边形,它的内角和为(n-2)180。,有两种方法可以证明这个结论。
(1)设θi为顶点i的内角,很明显,θi≤ 180。(假设多边形是凸的)。在每个顶点上,补角为(180-θi)。,对于一个封闭的凸多边形,全部顶点的补角之和为360。,有:
(2)任意n个顶点的凸多边形都能分解为n-2个三角形,由经典几何知识可知,三角形内角和为180。。所有三角形的内角和为(n-2)180。,可以看到,这个和总是等于多边形的内角和。
不幸的是,凹多边形和凸多边形一样,内角和也是(n-2)180。。怎样才能进一步判断一个多边形是不是凸多边形呢?对一个凸多边形,内角不会大于外角。(外角不是补角,一对内角外角的和等于360。)
所以,将每个顶点处较小的角(内角或外角)相加,凸多边形得到(n-2)180。,凹多边形则小于它。怎样判断哪个角较小呢?幸运的是,有这样一个工具 ---- 点乘,这种方法返回的角总是以较短的弧度来度量的。
下面的代码说明了怎样用角度和来判断多边形是否为凸多边形。
// Function to determine if a polygon is convex. The polygon is
// assumed to be planar.
//
// Input:
// n Number of vertices
// vl pointer to array of of vertices
bool isConvex( int n, const Vector3 vl[])
{
// Initialize sum to 0 radians
float angleSum = 0.0f;
// Go around the polygon and sum the angle at each vertex
for ( int i = 0 ; i < n ; ++i)
{
// Get edge vectors. We have to be careful on
// the first and last vertices. Also, note that
// this could be optimized considerably…
Vector3 e1;
if (i == 0)
e1 = vl[n–1] – vl[i];
else
e1 = vl[i–1] – vl[i];
Vector3 e2;
if (i == n–1)
e2 = vl[0] – vl[i];
else
e2 = vl[i+1] – vl[i];
// Normalize and compute dot product
e1.normalize();
e2.normalize();
float dot = e1 * e2;
// Compute smaller angle using “safe” function that protects
// against range errors which could be caused by numerical imprecision
float theta = safeAcos(dot);
// Sum it up
angleSum += theta;
}
// Figure out what the sum of the angles should be, assuming
// we are convex. Remember that pi/2 rad = 180 degrees
float convexAngleSum = ( float )(n – 2) * kPiOverTwo;
// Now, check if the sum of the angles is less than it should be;
// then we’re concave. We give a slight tolerance for numerical imprecision
if (angleSum < convexAngleSum – ( float )n * 0.0001f)
{
// We’re concave
return false ;
}
// We’re convex, within tolerance
return true ;
}
另一种检测凸性的方法是检测多边形上是否有凹点,如果一个都没有找到,就是凸多边形。它的基本想法是每个顶点的转向应该一致,任何转向不一致的点都是凹点。
怎样检测一个点的转向呢?技巧是利用边向量的叉乘,左手坐标系中,如果向量的转向是顺指针,它们的叉乘就会指向你。什么是指向你呢?我们从多边形的正面看,正面由法向量指明。如果没有提供法向量,就必须做一些计算来得到。一旦有了法向量,检查多边形的每个顶点。用相邻的两个边向量计算该顶点的法向量,接着用多边形的法向量和顶点的法向量点乘,检测它们的方向是否相反。如果是(点乘为负),那么这个顶点就是一个凹点。
三角分解和扇形分解
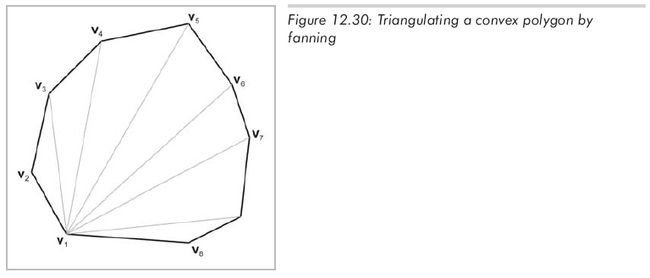
任意多边形都能分解为三角形。因此,所有对三角形的操作都能应用到多边形上。复杂、自相交、甚至简单的凹多边形的三角分解都不是一件简单的工作。幸运的是,简单多边形的三角分解是一件容易的事。一种显而易见的三角分解技术是选取一个点(称作第一个点),沿着顶点按"扇形"分解多边形。给定一个有n个顶点的多边形,沿多边形列顶点v1...vn,能够很容易地构造形如{v1,vi-1, vi}的n-2个三角形,见图12.30。
扇形三角分割会分割出一些长的、较细的三角形,这在某些情况下会引起麻烦。如同计算表面的法向量一样,数值的不精确性在度量极小的角时会造成一些问题。
一种更加"聪明"的分解方法是:连接两顶点的对角线将一个多边形分解为两部分。这时,对角线端点处的两个内角都能分解为两个新的内角。因此,总共产生了4个新内角。为了分解多边形,选择能使这4个新内角中最小的角最大化的对角线,用这条对角线将多边形分为两个。对分割后的每一部分都递归应用这个过程直到剩下的都是三角形。
这个方法产生较少的细三角形,但在实践中,它过于复杂。根据几何学和应用目的,扇形分解已经足够了(并且简单得多)。