堆排序
堆排序(Heapsort)是指利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构,并同时满足堆性质:即子结点的键值或索引总是小于(或者大于)它的父节点。
| 分类 | 排序算法 |
|---|---|
| 数据结构 | 数组 |
| 最差时间复杂度 | |
| 最优时间复杂度 | |
| 平均时间复杂度 | |
| 最差空间复杂度 | |
| 最佳算法 | 不是 |
堆节点的访问
通常堆是通过一维数组来实现的。在起始阵列为 0 的情形中:
- 堆的根节点(即堆积树的最大值)存放在阵列位置 1 的地方;
注意:不使用位置 0,否则左子树永远为 0[2]
- 父节点i的左子节点在位置 (2*i);
- 父节点i的右子节点在位置 (2*i+1);
- 子节点i的父节点在位置 floor(i/2);
堆的操作
在堆的数据结构中,堆中的最大值总是位于根节点。堆中定义以下几种操作:
- 最大堆调整(Max_Heapify):将堆的末端子结点作调整,使得子结点永远小于父结点
- 建立最大堆(Build_Max_Heap):将堆所有数据重新排序
- 堆排序(HeapSort):移除位在第一个数据的根结点,并做最大堆调整的递回运算
阵列堆积排序
#include <cstdio>
#include <cstdlib>
#include <cmath>
const int HEAP_SIZE = 13; //堆積樹大小
int parent(int);
int left(int);
int right(int);
void Max_Heapify(int [], int, int);
void Build_Max_Heap(int []);
void print(int []);
void HeapSort(int [], int);
/*父結點*/
int parent(int i)
{
return (int)floor(i / 2);
}
/*左子結點*/
int left(int i)
{
return 2 * i;
}
/*右子結點*/
int right(int i)
{
return (2 * i + 1);
}
/*單一子結點最大堆積樹調整*/
void Max_Heapify(int A[], int i, int heap_size)
{
int l = left(i);
int r = right(i);
int largest;
int temp;
if(l < heap_size && A[l] > A[i])
{
largest = l;
}
else
{
largest = i;
}
if(r < heap_size && A[r] > A[largest])
{
largest = r;
}
if(largest != i)
{
temp = A[i];
A[i] = A[largest];
A[largest] = temp;
Max_Heapify(A, largest, heap_size);
}
}
/*建立最大堆積樹*/
void Build_Max_Heap(int A[])
{
for(int i = (HEAP_SIZE-1)/2; i >= 0; i--)
{
Max_Heapify(A, i, HEAP_SIZE);
}
}
/*印出樹狀結構*/
void print(int A[])
{
for(int i = 0; i < HEAP_SIZE;i++)
{
printf("%d ", A[i]);
}
printf("\n");
}
/*堆積排序程序碼*/
void HeapSort(int A[], int heap_size)
{
Build_Max_Heap(A);
int temp;
for(int i = heap_size - 1; i > 0; i--)
{
temp = A[0];
A[0] = A[i];
A[i] = temp;
Max_Heapify(A, 0, i);
}
print(A);
}
/*輸入資料並做堆積排序*/
int main(int argc, char* argv[])
{
int A[HEAP_SIZE] = {19, 1, 10, 14, 16, 4, 7, 9, 3, 2, 8, 5, 11};
HeapSort(A, HEAP_SIZE);
system("pause");
return 0;
}
C++语言
堆的结构采用阵列实现,起始索引为0。
#include <iostream>
using namespace std;
/*
#堆排序#%
#数组实现#%
*/
//#筛选算法#%
void sift(int d[], int ind, int len)
{
//#置i为要筛选的节点#%
int i = ind;
//#c中保存i节点的左孩子#%
int c = i * 2 + 1; //#+1的目的就是为了解决节点从0开始而他的左孩子一直为0的问题#%
while(c < len)//#未筛选到叶子节点#%
{
//#如果要筛选的节点既有左孩子又有右孩子并且左孩子值小于右孩子#%
//#从二者中选出较大的并记录#%
if(c + 1 < len && d[c] < d[c + 1])
c++;
//#如果要筛选的节点中的值大于左右孩子的较大者则退出#%
if(d[i] > d[c]) break;
else
{
//#交换#%
int t = d[c];
d[c] = d[i];
d[i] = t;
//
//#重置要筛选的节点和要筛选的左孩子#%
i = c;
c = 2 * i + 1;
}
}
return;
}
void heap_sort(int d[], int n)
{
//#初始化建堆, i从最后一个非叶子节点开始#%
for(int i = n / 2; i >= 0; i--)
sift(d, i, n);
for(int i = 0; i < n; i++)
{
//#交换#%
int t = d[0];
d[0] = d[n - i - 1];
d[n - i - 1] = t;
//#筛选编号为0 #%
sift(d, 0, n - i - 1);
}
}
int main()
{
int a[] = {3, 5, 3, 6, 4, 7, 5, 7, 4}; //#QQ#%
heap_sort(a, sizeof(a) / sizeof(*a));
for(int i = 0; i < sizeof(a) / sizeof(*a); i++)
{
cout << a[i] << ' ';
}
cout << endl;
return 0;
}
in-place堆排序
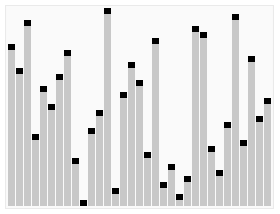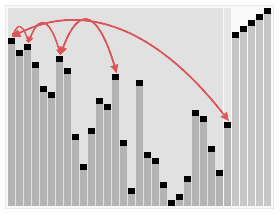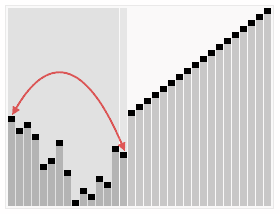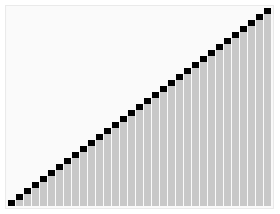
基于以上堆相关的操作,我们可以很容易的定义堆排序。例如,假设我们已经读入一系列数据并创建了一个堆,一个最直观的算法就是反复的调用del_max()函数,因为该函数总是能够返回堆中最大的值,然后把它从堆中删除,从而对这一系列返回值的输出就得到了该序列的降序排列。真正的in-place的堆排序使用了另外一个小技巧。堆排序的过程是:
- 建立一个堆H[0..n-1]
- 把堆首(最大值)和堆尾互换
- 把堆的尺寸缩小1,并调用
shift_down(0),目的是把新的数组顶端数据调整到相应位置 - 重复步骤2,直到堆的尺寸为1
平均复杂度
堆排序的平均时间复杂度为,空间复杂度为
。