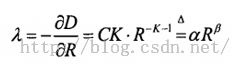HEVC码率控制算法研究与HM相应代码分析(二)——新的码率控制模型
在H.264以及之前的码率控制算法中,R-Q模型得到了广泛的使用,这一模型认为Q是决定码率的主要因素。但研究发现,只有当所有除了Q以外其他的编码参数均固定的情况下,这一假设才是成立的。在实际应用中,如果其他的编码参数并不是十分灵活,这一假设还是基本成立的。但随着视频编码技术的发展,这一假设对于越来越灵活的编码框架来说,并不成立。例如,HEVC通过CU的四叉树分割和TU的四叉树分割,比先前其他的视频编码标准支持更为灵活的模式组合,此时再认为Q是决定R的主要因素,并不十分恰当。
研究认为利用R-Q模型进行码率控制存在诸多问题。
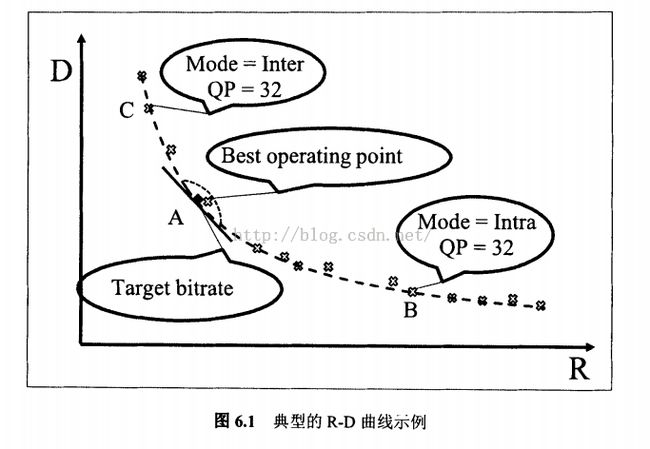
(1)R是由编码器通过选择编码参数组合决定的,编码参数包括QP和许多其他如模式和运动信息等参数。事实上,在R和Q之间并不存在一一对应的关系。如下图中的B和C都是最优点,并且两个点使用了相同的QP,但是用了不同的编码模式,这说明R和QP之间并没有一一对应的关系。
(2)在R-Q模型中反复出现的蛋鸡悖论问题:为了达到某一预定的码率,必须要先获得残差信息才可以决定合适的QP值。但是,残差信息只有在模式选择和运动估计等过程完成后才能够确定,这样在模式选择过程中需要使用一个预先决定的QP值。而HEVC中有更多更灵活的模式,使得应用R-Q模型更加困难,应该研究另一种思路摆脱蛋鸡悖论的问题。
(3)QP是应当由RDO过程进行优化的参数之一,并不应当在RDO过程之前由码率控制算法决定。只有在包括QP的所有参数均由RDO过程进行选择的情况下,才可以达到最优的R-D性能。
(4)QP仅能选择整数,并且对于H.264/MPEG-4 AVC和HEVC来说,QP每增加6时量化步长增加一倍。QP仅能选取一些离散值,这也制约了通过调整QP来达到目标码率的精确度。
为了得出R-λ模型,首先就R-D关系的指数模型
和双曲模型

进行对比。对比实验中使用仅使用一幅参考图片IBBB编码结构,并且所有的B帧都是用相同的QP值,然后对若干序列使用HM7(不打开码率控制功能)进行测试,然后分别使用两种模型拟合R-D(bpp-MSE)曲线,最后的结论是双曲模型比指数模型可以更精确的刻画HEVC的R-D模型。
接下来就以双曲模型为基础进行推导,我们知道λ是R-D曲线的斜率,于是得到下式
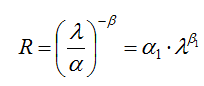
α和β是和序列特性有关的参数。实验也证明了该模型的准确性,于是后面的码率控制框架都基于这个R-λ模型展开。
从几何意义上来说,率失真优化问题就是在R-D曲线上选择最优工作点,而λ即为曲线切线的斜率,所以它才是与最优工作点一一对应的值。此外,可以证明
(1) 决定λ的值和RDO过程并没有任何相互依赖性,可以依据目标比特在RDO之前决定。
(2) λ值同样会影响非残差比特。当λ值较大时,编码器倾向于选择大粒度的模式(比如大的分块方式),这样,消耗在表示非残差信息上的比特也会相对较少:反之,亦然。而QP值只会影响残差信息的比特数。
(3) λ并不像QP值那样,所以它的调整可以更精细
与之前的分析类似,在码率控制的每一层我们有不同的关注点,但是在每一层都要关注前一单元与后面剩余单元的率失真性能的依赖关系。
本文介绍了HEVC中全新的R-λ模型,下一篇文章将介绍基于这一模型的码率控制算法,并对HM中对应的代码进行分析。