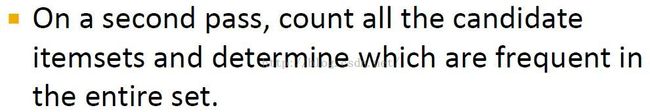海量数据挖掘MMDS week2: 频繁项集挖掘 Apriori算法的改进：非hash方法

http://blog.csdn.net/pipisorry/article/details/48914067

海量数据挖掘Mining Massive Datasets(MMDs) -Jure Leskovec courses学习笔记之关联规则Apriori算法的改进：非hash方法 - 大数据集下的频繁项集：挖掘随机采样算法、SON算法、Toivonen算法

Apriori算法的改进：大数据集下的频繁项集挖掘

1. 前面所讨论的频繁项都是在一次能处理的情况。如果数据量过大超过了主存的大小，这就不可避免的得使用k步来计算频繁项集。这里有许多应用并不需要发现所有的频繁项。比方说在超市，我们只要找到大部分的销售频繁关联项就够了，而不必找出所有的频繁项。

2. Apriori算法在计算频繁多项集时，要一步一步计算，会有相当多的频繁项集产生。这样主存可能存在不足的痛苦。An alternative is to compress all the work into one or two passes.But It may have both false positives and false negatives.But if the data cooperates there will not be too many of either.

基于采样的方法。基于前一遍扫描得到的信息，对此仔细地作组合分析，可以得到一个改进的算法，Mannila等先考虑了这一点，他们认为采样是发现规则的一个有效途径。

基于划分的方法。Savasere等设计了一个基于划分(partition)的算法.这个算法先把数据库从逻辑上分成几个互不相交的块，每次单独考虑一个分块并对它生成所有的频集，然后把产生的频集合并，用来生成所有可能的频集，最后计算这些项集的支持度。这里分块的大小选择要使得每个分块可以被放入主存，每个阶段只需被扫描一次。而算法的正确性是由每一个可能的频集至少在某一个分块中是频集保证的。

Note: 算法可行的标准是：几乎没有false negatives(频繁项集当做非频繁项集)和false positives(非频繁项集被判为频繁项集)。

皮皮blog

随机采样算法(基于采样的方法)

简单的随机采样算法

不是使用整个文件或篮子，我们使用篮子的一个子集的集合并假装他们是整个数据集，并调整支持度的阈值来适应小篮子。

基本思路就是：先采样部分basket，在其上运行Apriori(PCY...)算法，并调整相应支持度阈值。

  

Note: 采样得到的子数据集直接存入主存，第一次载入主存后，之后扫描数据子集就不用再次进行I/O操作了。

采样方式

最安全的抽样方式是读入整个数据集，然后对于每个篮子，使用相同的概率p选择样品。假设这有m个篮子在整个文件中。在最后，我们需要选择的样品的数量接近pm个篮子的样品数。

但是如果我们事先知道这些篮子本身在文件中就是随机放置的，那么我们就可以不用读入整个文件了，而是只接选择前面的pm个篮子作为样品就可以了。或者如果文件是分布式文件系统，我们可以选择第一个随机块作为样品。

采样大小

We choose some set of the baskets,not more than we'll fill perhaps half the main memory.
支持度阈值

我们使用篮子的一个子集并假装他们是整个数据集。我们必须调整支持度的阈值来适应我们的小篮子。例如，我们针对完整数据集的支持度阈值为s，当我们选择1%的样本时，我们可以在支持度阈值为s/100的度量上测试。

当我们的样品选择完成，我们可以使用部分的主存来放置这些篮子。剩下的主存用来执行前面的Apriori、PCY、Multistage或Multihash算法。当然这些算法必须运行所有的样品，在每个频繁集上，直到找不到频繁集为止。这个方法在执行读取样品时不需要磁盘操作，因为它是驻留在内存的。当每个频繁项被发现，它们就可以写到磁盘上了。

减少错误的随机采样算法

抽样可能导致是频繁项的没有放进频繁集，也存在非频繁项的放入了频繁集。

当样本足够大时，问题变得不是那么严重了；那些支持度远大于阈值的项集即使在样本中其支持度也会很高，所有误分的可能性不大。但是那些支持度在阈值附近的就不好说了。

避免非频繁项集被判为频繁项集false positives

简单的随机采样算法并不需要对完整的大数据集进行一次扫描，但是我们可以通过对整个数据集的一遍扫描，计算所有样品中频繁项集的支持度，保留那些在样品和在数据集上支持度都高于阈值的频繁项集，以此避免非频繁项集被判为频繁项集的错误。然而这种方法不能避免那些是频繁集却被当做非频繁项集的情况。

减少频繁项集当做非频繁项集的数量false negatives

但是我们可以减少那些是频繁项集却没有在样品中找出的数量如果内存的数量允许。我们设想如果s是支持阈值，且样品相对于整个数据集的大小为p，这样我们可以使用ps作为支持阈值。然而我们可以使用比这个值稍微小点的值作为阈值，如0.9ps。使用更低的阈值的好处是能使更多的项进入到频繁集中，这样就可以降低这种错误。The disadvantage of lowering the support threshold is that then you have to count more sets and there may not be enough main memory to do so.

然后再到整个数据集中计算这些频繁项集的实际支持度(But then on the full pass you use the correct threshold s when counting from the entire set)，除去那些非频繁项集，这样我们就可以消除非频繁项集当成频繁项集的错误，同时最大化的减少了频繁项集被当做了非频繁项集。

皮皮blog

SON算法(Savasere,Omiecinski, and Navathe; 基于划分的方法)

{an improvement on the simple algorithm.SON方法能够对数据集上所有数据进行处理}

SON算法同时避免了false negatives(频繁项集当做非频繁项集)和false positives(非频繁项集被判为频繁项集)，所带来的代价是需要两个完全的步骤。

SON基本思想

将输入文件划分成1/p个块(chunks)。将每个文件块作为一个样本，并执行Apriori算法在其块上。同样的使用ps作为其阈值。将每个块找到的频繁项集放到磁盘上。

第一步处理

找到局部频繁项集：一旦所有的块按此方式被处理，将那些在一个或多个块中被选中的频繁项集收集起来作为候选频繁项集。注意，如果一个项集在所有的块中都不是频繁项集，即它在每个块中的支持度都低于ps。因为块数为1/p，所以，整体的支持度也就低于(1/p)ps=s。这样，每个频繁项集必然会出现在至少一个块的频繁项集中，于是，我们可以确定，真正的频繁项一定全在候选频繁项集中，因此这里没有false negatives。当我们读每个块并处理它们后，我们完成一次处理。

第二步处理

找到全局频繁项集：我们计算所有的候选频繁项集，选择那些支持度至少为s的作为频繁项集。

分布式SON算法

分布式算法步骤解析

The idea is that you break the file containing the baskets into many groups,one at each processor.

Each processor finds the local frequent item sets,then broadcast to each other processor its list of local frequent item sets.The union of all these lists is the candidate item sets.Now each processor knows the list of candidate itemvsets and counts them locally.

Then, each processor broadcasts its counts to all the other processor.Now each processor knows the total count for each candidate set and can discover which of them are truly frequent.

SON算法与Map-Reduce

SON算法使得它很适合在并行计算的环境下发挥功效。每个块可以并行的处理，然后每个块的频繁集合并形成候选集。我们可以将候选分配到多个处理器上，在每个处理器上，这些处理器只需要在一个“购物篮”子集处理这些发过来的候选频繁项集，最后将这些候选集合并得到最终的在整个数据集上的支持度。这个过程不必应用map-reduce，但是，这种两步处理的过程可以表达成map-reduce的处理。

map-reduce-map-reduce流程

FirstMap Function：分配篮子子集，并在子集上使用Apriori算法找出每个项集的频繁度。将支持阈值降从s降低到ps，如果每个Map任务分得的部分占总文件的比例为p。map的输出为key-value对(F,1)，这里F为该样本的频繁项集。值总是为1，这个值是无关紧要的。

FirstReduce Function：每个reduce任务被分配为一组key，这组key实际就为项集，其中的value被忽略，reduce任务简单产生这些出现过一次或多次的项集，将其作为候选频繁项集作为输出。

SecondMap Function：第二步的map任务将第一步的reduce的所有输出和输入文件的一部分作为输入，每个Map任务计算在分配的那块输入文件中每个候选频繁项集的出现次数。这步的输出为键值对(C，v)，这里，C是一个候选集，v是其在该Map任务中的支持度。

SecondReduce Function：此步的Reduce任务将在每个候选频繁项集各个Map中的候选集的支持度相加。相加的结果就为整个文件上的支持度，这些支持度若大于s，则保留在频繁项集中，否则剔除。

皮皮blog

Toivonen算法(随机抽样算法)

{an entirely different approach to saving passes}

Toivonen算法在给出足够内存的情况下，在小样本上进行一步处理，接着再整个数据上进行一步处理。这个算法不会带来false negatives，也不会带来false positives，但是这里存在一个小的概率使得算法会产生不了任何结构。这种情况下算法需要重复直至找到一个结果，虽然如此，得到最终频繁项集的处理的平均步数不会太大。

小样本上扫描pass1：寻找候选频繁项集

Toivonen算法由从输入数据集中选择一个小的样品开始，并从中找到候选频繁项集，找的过程同Apriori算法，不过很重要的一点不同是阈值的设置的比样品比例的阈值小。即，当整个数据集上的支持度阈值为s，该样品所占数据集的比例为p，则该阈值可以设置为0.9ps或0.8ps。越小的阈值，就意味着在处理样本时，越多的内存在计算频繁项集时需要使用；但是也就越大的可能性避免算法不能产生结果。

构造负边界negative border

Negative border：是样品的一个非频繁项集合，并且这些项集去掉任意一个项item后的直接子集是频繁集。

构造Negative border示例

考虑项为{A,B,C,D,E}，而且我们找到频繁项集为{A}，{B}，{C}，{D}，{B，C}，{C，D}。

注意，只要篮子数不比阈值小，空集Φ也是频繁的，但是我们忽略它。The empty set is a subset of every basket, so the only way the empty set could not be frequent is if the support threshold is higher than the number of baskets.But that means nothing would be frequent and why are we bothering anyway.

首先，{E}是在negative border中的，因为{E}本身不是频繁项集，但是从中去任意项后就变成Φ了，就成了频繁项集，所有包含在negative border中。

{A，B}，{A，C}，{A，D}和{B，D}也在negative border中。因为它们都不是频繁项集，但是除掉一个项的子集都是频繁项集。如{A，B}的子集{A}和{B}都是频繁集。

剩下的六个二元项集不在negative border中。{B，C}和{C，D}因为它们本身是频繁项集，所有就不是negative border的元素了，而其他四个虽然不是频繁项集，但是因为包含了项E，而子集{E}不是频繁项集。

没有任何三元的或更大的项集在negative border中了。例如{B，C，D}不在negative border中，因为它有一个立即子集{B，D}，而{B，D}不是频繁项集。

这样，negative border由下面五个集合组成：{E}，{A，B}，{A，C}，{A，D}和{B，D}。

Negative border的作用及目的

The purpose of counting the negative border is to act as canaries.None of them should be frequent in the whole data set because we picked the support threshold for the sample that is significantly below a proportional threshold.

But if one or more of the items sets in the negative order turned out to be frequent in the hold,then we have to believe that the sample was not representative.And we need to repeat the entire process.

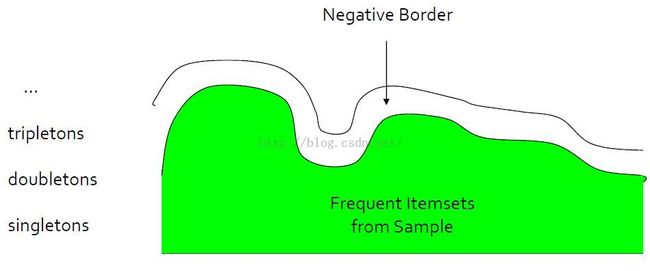
Negative border图解

Note:

1. the vertical dimension is the size of item sets, and the horizontal dimension somehow represents all the item sets of a given size.

2. The frequent item region is closed downwards because of monotonicity,a subset of the frequent item set is always frequent.

3. The negative border may consist of sets of different sizes, and its items tend to have widely varying frequencies.
大数据集上扫描pass2

我们需要进一步在整个数据集上处理，算出所有在样品中的频繁项集或negative border中的所有项集的计数。

这步会产生的可能输出为：

1、  如果negative border中没有一个项集在整个数据集上计算为频繁项集。这种情况下，正确的频繁项集就为样本中的频繁项集。

2、  某些在negative border中的项集在整个数据集中计算是频繁项集。这时，我们不能确定是否存在更大的项集，这个项集既不在样本的negative border中，也不在它的频繁项集中，但是是整个数据集的频繁项集。这样，我们在此次的抽样中得不到结果，算法只能在重新抽样，继续重复上面的步骤，直到出现满足输出情形1时停止。

Note:如果negative border发现某个项集在整个数据集中是频繁的，那么它的super sets都可能是频繁项集，而被我们忽略了。这样的话就必须重新采样运行算法。

尽量避免第2种情况发生的方法：Try to choose the support threshold so the probability of failure is low, while the number of itemsets checked on the second pass fits in main memory.

Toivonen算法可行性分析

显然 Toivonen算法不会产生false positive，因为它仅仅将在样本中是频繁项并在整个数据集上计算确实为频繁项集的项集作为频繁项集。

讨论Toivonen算法能够不产生false negative

如果一个项集在整个数据集上是频繁的，而在样本中不是频繁的，那么negative border中一定有一个成员是频繁的。（这样就要重新运行算法了）

也就是说如果在negative border中没有成员在整个数据集中是频繁的，那么在整个数据集中再也不存在我们没有计数的频繁项了。if we find no members of the negative border to be frequent in the whole, then we know that there are no sets at all that are frequent in the whole but that we did not count.

也就是说不存在一个项集在整个数据集上是频繁的，而在样本中既不出现在频繁集中，也不出现在negative border中。

定理证明proof by contradiction

Note:

1. In principle, T could be S itself,if it has no proper subsets that are not frequent in the sample.All we care about is that all the subsets of T are frequent in the sample.

2. I also claim that T is in the negative border.If it is not frequent in the sample, but it had a proper subset that was not frequent in the sample,then T would not be the smallest subset of S with that property.也就是S的比T更小的子集一定在样本频繁项集中，这样T就自然在样本的negative border上了。T就在样本的negative border上并且T是频繁的 与 2.Nothing ...矛盾！

反例：

假设这里有个集合S在数据集上是频繁项集，也不是样本的频繁项集。并且negative border中没有成员在整个数据集上是频繁的。

假设T是S的一个在样本中不属于频繁项集的最小子集。

由频繁项集的单调性知，S的所有子集都是整个数据集的频繁项集。则T是整个数据集的频繁项集。
T一定在negative border中。因为T满足在negative border中的条件：它自己不是样本的频繁项集，而它的直接子集是样本的频繁项集，因为若它的直接子集不是，则T就不是S的在样本中不属于频繁项集的最小子集（这个直接子集才是）。
于是我们发现T是整个数据集的频繁项集，又在样本的negative border中。与假设矛盾！

皮皮blog

其他的频集挖掘方法

上面我们介绍的都是基于Apriori的频集方法。即使进行了优化，但是

Apriori方法一些固有的缺陷无法克服

可能产生大量的候选集。当长度为1的频集有10000个的时候，长度为2的候选集个数将会超过10M。还有就是如果要生成一个很长的规则的时候，要产生的中间元素也是巨大量的。

无法对稀有信息进行分析。由于频集使用了参数minsup，所以就无法对小于minsup的事件进行分析；而如果将minsup设成一个很低的值，那么算法的效率就成了一个很难处理的问题。

分别解决以上两个问题的两种方法：

FP-树频集算法

针对问题一，J.Han等在《数据挖掘概率与技术》中提出了不产生候选挖掘频繁项集的方法：FP-树频集算法。他们采用了分而治之的策略，在经过了第一次的扫描之后，把数据库中的频集压缩进一棵频繁模式树（FP-tree），同时依然保留其中的关联信息。随后我们再将FP-tree分化成一些条件库，每个库和一个长度为1的频集相关。然后再对这些条件库分别进行挖掘。当原始数据量很大的时候，也可以结合划分的方法,使得一个FP-tree可以放入主存中。实验表明，FP-growth对不同长度的规则都有很好的适应性，同时在效率上较之apriori算法有巨大的提高。

挖掘高可信度的规则

第二个问题是基于这个的一个想法：apriori算法得出的关系都是频繁出现的，但是在实际的应用中，我们可能需要寻找一些高度相关的元素，即使这些元素不是频繁出现的。在apriori算法中，起决定作用的是支持度，而我们现在将把可信度放在第一位，挖掘一些具有非常高可信度的规则。Edith Cohen在"Finding Interesting Associations without Support Pruning"中介绍了对于这个问题的一个解决方法。

整个算法基本上分成三个步骤：计算特征、生成候选集、过滤候选集。在三个步骤中，关键的地方就是在计算特征时Hash方法的使用。在考虑方法的时候，有几个衡量好坏的指数：时空效率、错误率和遗漏率。

基本的方法有两类：Min_Hashing(MH)和Locality_Sensitive_Hashing(LSH)。

Min_Hashing的基本想法是：将一条记录中的头k个为1的字段的位置作为一个Hash函数。Locality_Sentitive_Hashing的基本想法是：将整个数据库用一种基于概率的方法进行分类，使得相似的列在一起的可能性更大，不相似的列在一起的可能性较小。我们再对这两个方法比较一下。MH的遗漏率为零，错误率可以由k严格控制，但是时空效率相对的较差。LSH的遗漏率和错误率是无法同时降低的，但是它的时空效率却相对的好很多。所以应该视具体的情况而定。最后的实验数据也说明这种方法的确能产生一些有用的规则。

Dic算法

DIC 算法

DIC算法实现（包括测试数据） 

皮皮blog

Reviews复习

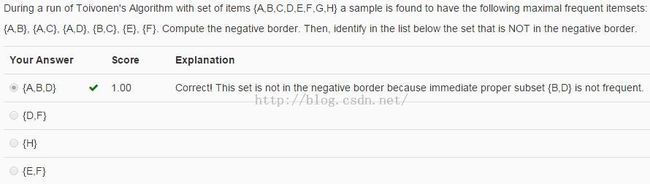
Toivonen算法

Note: 频繁项集的子集也是频繁的，这样频繁项集还包含{D} 。但是不会包含{B, D}

from:http://blog.csdn.net/pipisorry/article/details/48914067

ref:

DIC 算法

DIC算法实现（包括测试数据）