huffman编码实现（详细实现）

1、概述

     huffman编码是一种可变长编码（  VLC：variable length coding)）方式，于1952年由huffman提出。依据字符在需要编码文件中出现的概率提供对字符的唯一编码，并且保证了可变编码的平均编码最短，被称为最优二叉树，有时又称为最佳编码。

2、原理

    在了解huffman树为最优二叉树时，先要明确下面几个概念：

    路径长度:树中一个节点到另一个节点之间分支构成这两个节点之间的路径，路径上的分支数目为其路径长度。

    树的路径长度:树根到每一个节点的路径长度之和 为 “l”。

     节点的带权路径长度:节点到树根之间的路径长度与节点上权的乘积。

                                                                                                          n

     树的带权路径长度:所有节点的带权路径长度之和，记作 WPL = ∑wk  *  lk 。

                                                                                                         k=1

    n个节点，权值为{ w1,  w2, - - -,wn }，把此n个节点为叶子节点，构造一个带n个节点叶子节点的二叉树，每个叶子节点的带权路径长度为wi。

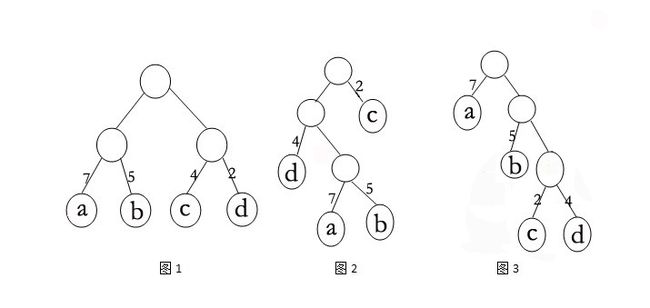
取节点a,b,c,d 其w[] = {2, 5, 7, 4}，a=7 构造如下三棵树为例：

  图1：wpl = 7*2 +5*2 + 2*2 + 4*2 = 36

  图2：wpl = 7*3 + 5*3 + 2*1 + 4*2 = 46

  图3：wpl = 7*1 + 5*2 + 2*3 + 4*3 = 35

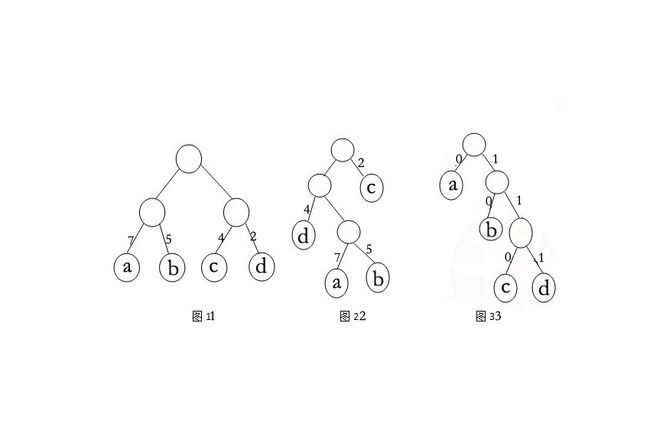
  可以证明（图3）其带权路径长度最短，就是huffman树。依次为两节点的连接线编码，左孩子为0，右孩子为1。那么图3就变成了（图33）：

  编码如下：a（0）、b（10）、c（110）、d（111）

  不知道是否有人会问为什么a、b、c、d都是树的叶子节点，而不存在某个是父节点呢？试想，如果a是c、d的父节点，假设a的编码为0，其左右孩子是b、c，那么b，c的编码分别是00，和01，那么当出现诸如010001的压缩串时，可分别解释为caac，cbc，因为在出现a时，如果后面的编码为0，则不确定是解释为aa还是b了，出现歧义就出问题，所以字符只能出现在叶子节点。

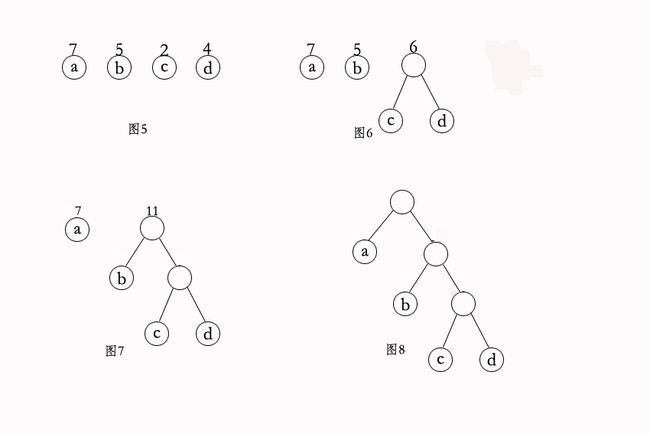
  在上面我们必须保证须编码的字符必须出现叶子节点，那我们怎么保证（图33）就是最短带权路径呢？我们下面一步步走下去构造huffman树，我们还假设a、b、c、d的带权为7、5、2，4。

3、构造huffman树过程

  构造huffman树的哈夫曼算法如下：

  （1）n节点的权值｛w1、w2、·····，wn｝构成n棵二叉树集合F=｛T1，T2，···，Tn｝，每棵二叉树Ti只有一个带权为Wi的根节点，左右孩子均空。

  （2）在F中选取两棵根节点权值最小的作为树的左右孩子构造一棵新的二叉树，且置根节点的权值为左右孩子权值之和，在F中删除这两棵树，新二叉树之于F中

  （3）重复（2），直到F中只有一棵树为止，这棵树就是huffman树。

  上面就是以abcd四个节点构造huffman树的过程。

4、huffman代码（如下）

// Huffman coding.cpp : 定义控制台应用程序的入口点。
//Copyright@Qyee, 2011-7-30

#include "stdafx.h"
#include <iostream>
#include <Windows.h>

using namespace std;

//huffman tree节点定义
typedef struct
{
	int weight;					//保存权值
	int parent, lchild, rchild;	//保存左右孩子的节点值
}HuffmanNode, *HuffmanTree;

typedef char **HuffmanCode;

void HuffmanCoding(HuffmanTree &HT, int *w, int n);	//Huffman编码函数
void select(HuffmanTree HT,int n, int &s1, int &s2);//选择书中节点值较小的两个节点
void Error(char* message);		//显示错误信息

int w[] = {2, 5, 7, 4};	//各节点权值

int main(int argc, char* argv[])
{
	HuffmanTree HT;

	HuffmanCoding(HT, w, 6);

	getchar();	//在win7系统，防止直接跳出，接收字符才执行return语句
	return 0;
}

void HuffmanCoding(HuffmanTree &HT, int *w, int n)
{
	if (n <= 1)
		Error("code is small");
	int m = 2 * n - 1; //n nodes create huffman tree need 2n-1 nodes
	HT = (HuffmanNode*)malloc((m + 1) * sizeof(HuffmanNode));//Huffman tree的所有节点

	int s1, s2; //record the two mini weights nodes

	memset(HT, 0, (m + 1)* sizeof(HuffmanNode));	//对所有节点初始化为-0
	//set the n nodes
	for (int i = 1; i <= n; i++)
	{
		HT[i].weight = *w++;	//初始化各节点权值
	}

	//创建Huffman tree
	for(int i = n + 1; i <= m; ++i)
	{
		//选择剩余节点中权值较小的s1和s2
		select(HT, i - 1, s1, s2);
		HT[s1].parent = i;
		HT[s2].parent = i;
		HT[i].lchild = s1;
		HT[i].rchild = s2;
		HT[i].weight = HT[s1].weight + HT[s2].weight;
	}

	HuffmanCode HC;
	int start, c, f;
	HC = (HuffmanCode)malloc((n + 1) * sizeof(char*));
	char* cd = (char*)malloc(n * sizeof(char));
	cd[n - 1] = '\0';
	for(int i = 1; i <= n; ++i)
	{
		start = n - 1;
		for(c = i, f = HT[i].parent; f != 0; c = f, f = HT[f].parent)
			if (HT[f].lchild == c)
				cd[--start] = '0';
			else
				cd[--start] = '1';
		HC[i] = (char*)malloc((n - start) * sizeof(char));
		strcpy(HC[i], &cd[start]);
	}

	for (int i = 1; i <= n; i++)
	{
		cout<<HC[i]<<endl;
	}

	free(cd);
	free(HC);
	free(HT);
}

void Error(char* message)
{
	fprintf(stderr, "Error: %s(5s will exit)", message);
	cout<<"\n";
	Sleep(5000);
	exit(1);
}

void select(HuffmanTree HT, int n, int &s1, int &s2)
{
	s1 = 1;
	s2 = 1;
	int min  = 99999;
	int i;
	//选择未被使用的第一个节点，
	for (i = 1; i <= n; ++i)
	{
		if (HT[i].parent == 0)
		{
			min = HT[i].weight;
			break;
		}
	}

	//find the mini s1
	for (int p =  1; p <= n; ++p)
	{
		if(0 == HT[p].parent && min >= HT[p].weight)
		{
			s1 = p;
			min = HT[p].weight;
		}
	}

	//find the s2
	min = 99999;
	for (int q =  1; q <= n; ++q)
	{
		if(0 == HT[q].parent && min >= HT[q].weight )
		{
			if( q == s1)
				continue;
			s2 = q;
			min = HT[q].weight;
		}
	}
}

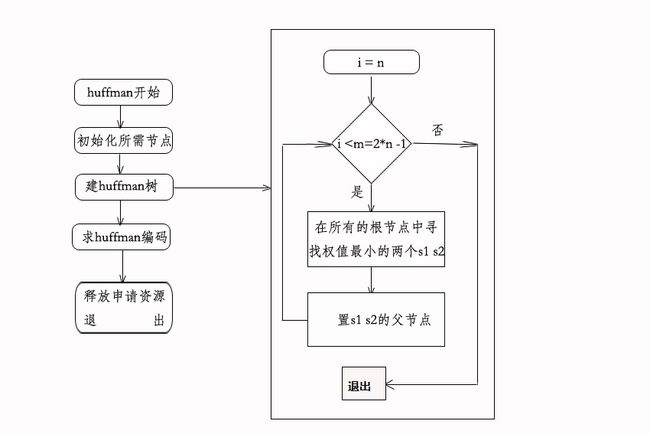
5、代码流程