用java实现Shazam 译文
翻译:[email protected] 2010/8/30
几天之前,我偶然看到一篇文章: How Shazam Works
这让我对shazam这样的程序是如何工作的产生了兴趣,更重要的一点是,(我想知道)用java实现类似的程序会有多难呢?
关于Shazam
Shazam是一款可以用来分析和配对音乐的程序。在手机上安装之后,拿着麦克风朝着音乐聆听大概20-30秒钟,它就能告诉你这是首什么歌曲。
我第一次用它的时候,它给了我一种魔法般的感觉。“它怎么做到的?”——甚至直到今天,在使用了如此久之后,我仍然有这种奇妙的感觉。
如果我们能自己写个东西,带来同样的感觉,这不是相当牛逼吗?于是,这就成了我上个周末的目标。
聆听!
第一步,取得音乐样本以供分析。我们首先要在java程序里面通过麦克风录入声音。这是我还没用java做过的事情,所以并不清楚这会有多困难。
但是最终证明这非常简单:
DataLine.Info info = new DataLine.Info(TargetDataLine.class, format);
final TargetDataLine line = (TargetDataLine) AudioSystem.getLine(info);
line.open(format);
line.start();
OutputStream out = new ByteArrayOutputStream();
running = true;
try {
while (running) {
int count = line.read(buffer, 0, buffer.length);
if (count > 0) {
out.write(buffer, 0, count);
}
}
out.close();
} catch (IOException e) {
System.err.println("I/O problems: " + e);
System.exit(-1);
}
float sampleRate = 44100;
int sampleSizeInBits = 8;
int channels = 1; //mono 单声道
boolean signed = true;
boolean bigEndian = true;
return new AudioFormat(sampleRate, sampleSizeInBits, channels, signed, bigEndian);
}
麦克风数据
接下来的挑战是分析数据。我将接收到的数据放到比特数组中,得到一个很长的数字列表,如下:
0
1
2
4
7
6
3
-1
-2
-4
-2
-5
-7
-8
(etc)
额,这玩意儿是声音么?
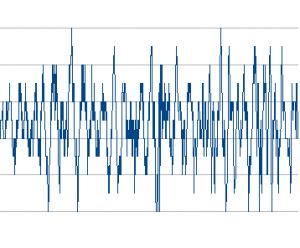
为知道这组数据能不能被可视化,我将它放到Open Office里生成一个线状图:
哈,当然!这种样子看上去就像是声音了。这和你在windows录音机里面看到的例子很像。
这样的数据其实叫做时域。但是这堆数字现在对我们来说根本没用。如果你读了上面提到的Shazam的文章,你会发现他们用到了频谱分析,而不是直接使用时域数据。
所以下一个大问题是:怎么把现在的数据转换到频谱分析数据呢?
离散傅里叶变换
为了转换当前数据成可用数据,我们应该执行一种称作离散傅里叶变换的操作。这将把数据从时域转换为频域。
但有一个问题,如果你把数据转换到了频域,会丢失每块数据的时间信息。所以你可以知道声音的所有的频率级别,但是你不知道他们对应于什么时候出现。
为解决这个问题,我们需要一个“滑动窗口”。我们每次取一块数据(我的例子里取的是4096字节),然后只转换这一块的信息。然后我们可以得到这4096字节数据里出现的所有频率信息。
实现它
为了不纠结于傅里叶变换这个概念,我google了一下,找到了一段快速傅里叶变换的代码(FFT)。在处理这一块数据的时候,进行如下调用:
byte audio[] = out.toByteArray();
final int totalSize = audio.length;
int amountPossible = totalSize/Harvester.CHUNK_SIZE;
//When turning into frequency domain we'll need complex numbers: 转换到频域,我们需要复数数组
Complex[][] results = new Complex[amountPossible][];
//For all the chunks: 遍历所有数据块
for(int times = 0;times < amountPossible; times++) {
Complex[] complex = new Complex[Harvester.CHUNK_SIZE];
for(int i = 0;i < Harvester.CHUNK_SIZE;i++) {
//Put the time domain data into a complex number with imaginary part as 0: 将时域数据放到复数数组里,复数的虚部设置为0
complex[i] = new Complex(audio[(times*Harvester.CHUNK_SIZE)+i], 0);
}
//Perform FFT analysis on the chunk: 对这块数据进行快速傅里叶变换
results[times] = FFT.fft(complex);
}
//Done! 搞定
现在我们拥有一个二维数组,存储了所有块的复数数组。这个数组包含了所有的频率信息。为将数据可视化,我决定实现一个完整的频谱分析器(仅仅为了确认我得到了正确的数字)。
为了展示数据,我把这些都放在一起:
for(int i = 0; i < results.length; i++) {
int freq = 1;
for(int line = 1; line < size; line++) {
// To get the magnitude of the sound at a given frequency slice
// get the abs() from the complex number.
// In this case I use Math.log to get a more managable number (used for color)
// 为了得到一个频率段内的声音强度,取复数的绝对值即可。这里我用了Math库的log函数来得到一个更好管理的数字(为了频谱图里的颜色值)
double magnitude = Math.log(results[i][freq].abs()+1);
// The more blue in the color the more intensity for a given frequency point:
// 颜色值里的蓝色分量越多,则给定的频率点的声音强度越高
g2d.setColor(new Color(0,(int)magnitude*10,(int)magnitude*20));
// Fill: 填充
g2d.fillRect(i*blockSizeX, (size-line)*blockSizeY,blockSizeX,blockSizeY);
// I used a improviced logarithmic scale and normal scale: 用了一个改进的对数比例和正常比例
if (logModeEnabled && (Math.log10(line) * Math.log10(line)) > 1) {
freq += (int) (Math.log10(line) * Math.log10(line));
} else {
freq++;
}
}
}
这好像有点跑题了,不过我仍要告诉你一个叫做Aphex Twin (Richard David James)的电子音乐家。他制作很疯狂的电子音乐,但是有些歌曲有一些很有趣的特点。比如他的大作, Windowlicker 里有一幅频谱图像。如果你把这个音乐的频谱图拿来观察,你会发现它看上去像是一个不错的漩涡。另外一首歌,Mathematical Equation则显示了Twin的脸!更多信息可以参见: Bastwood – Aphex Twin’s face.
现在我们用我的频谱分析器分析这歌曲,可以得到如下的结果:
不够完美,但是这看上去就是Twin的脸!
确定关键点
Shazam算法的下一个步骤是确定歌曲里的一些关键点。将这些关键点哈希,然后在他们800万首歌曲的数据库里面尝试进行匹配。这将会很快完成,因为哈希表的查找速度是O(1)。这也充分解释了Shazam令人吃惊的性能。
由于我想在一个周末内解决所有的问题(很杯具,这个是我的最大期限了,之后我有一个新的项目需要做),我尽可能的保持我的算法简单。让我吃惊的是它能正常工作。
针对频谱分析结果里的每一行,我取了特定(频率)范围内的最大声音强度值。在例子里是: 40-80, 80-120, 120-180, 180-300。
for (int freq = LOWER_LIMIT; freq < UPPER_LIMIT-1; freq++) {
//Get the magnitude: 得到声音强度
double mag = Math.log(results[freq].abs() + 1);
//Find out which range we are in: 找出是在哪一个频率范围内
int index = getIndex(freq);
//Save the highest magnitude and corresponding frequency: 保存最大的强度值和对应的频率
if (mag > highscores[index]) {
highscores[index] = mag;
recordPoints[index] = freq;
}
}
//Write the points to a file: 把点值写入文件
for (int i = 0; i < AMOUNT_OF_POINTS; i++) {
fw.append(recordPoints[i] + "\t");
}
fw.append("\n");
// ... snip ...
public static final int[] RANGE = new int[] {40,80,120,180, UPPER_LIMIT+1};
//Find out in which range 找出在哪个范围内
public static int getIndex(int freq) {
int i = 0;
while(RANGE[i] < freq) i++;
return i;
}
}
我们现在再录制一首歌,得到一张如下的数字列表:
30 41 84 146 199
33 51 99 133 183
33 47 94 137 193
32 41 106 161 191
33 76 95 123 185
40 68 110 134 232
30 62 88 125 194
34 57 83 121 182
34 42 89 123 182
33 56 99 121 195
30 41 84 146 199
33 51 99 133 183
33 47 94 137 193
32 41 106 161 191
33 76 95 123 185
(所有红点都是关键点)
索引我自己的歌曲
现在算法已经就绪,我决定索引我的3000首歌曲。可以直接打开mp3文件然后转换到正确的格式,用我们处理麦克风数据一样的方式进行读取,而不必再使用麦克风来录音。转换立体声音乐为单声道是一个我期待中的小把戏,具体的例子可以在网上找得到(这里贴出的话代码太多了点)。我不得不改变了一些取样。
匹配!
程序最重要的部分就是匹配过程了。看了Shazam的论文,他们用哈希值来配对,以此决定哪些歌才是最佳匹配。
为节省时间,我用我们数据中的一条线(例如33, 47, 94, 137)作为一组哈希值1370944733,而不是考虑困难的点对算法。(例子里用3或者4个点是工作最好的,但是调优很困难,因为每次都需要重新索引我的mp3文件)
例子里使用每条线的4个点做哈希:
private static final int FUZ_FACTOR = 2;
private long hash(String line) {
String[] p = line.split("\t");
long p1 = Long.parseLong(p[0]);
long p2 = Long.parseLong(p[1]);
long p3 = Long.parseLong(p[2]);
long p4 = Long.parseLong(p[3]);
return (p4-(p4%FUZ_FACTOR)) * 100000000 + (p3-(p3%FUZ_FACTOR)) * 100000 + (p2-(p2%FUZ_FACTOR)) * 100 + (p1-(p1%FUZ_FACTOR));
}
一个歌曲列表。List<String> (索引是歌曲ID,字符串是歌曲名songname)
哈希数据库。Map<Long, List<DataPoint>>
long类型的key代表了它自己的哈希值,它有对应的一个DataPoints的列表。
DataPoint结构是这样的:
private int time;
private int songId;
public DataPoint(int songId, int time) {
this.songId = songId;
this.time = time;
}
public int getTime() {
return time;
}
public int getSongId() {
return songId;
}
}
然后是读取我们需要匹配的歌曲的数据。(待识别样本的)哈希值被计算出来,我们就去查找匹配的点。
这有一个问题,对于每个哈希值,会有一些命中点(可能多于一个)。但是我们怎么来确定哪一个结果才是最终正确的歌曲呢?检查匹配的个数?不,这不行。
最重要的因素是时间。我们必须对时间进行重叠(把待识别样本的时间轴和索引时候的音乐样本的时间轴对应起来才知道是不是正确的歌曲)!
但是我们不知道他们位于歌曲的哪个位置(待识别样本具体开始于歌曲的哪个时间点是不一定的,用户可能在听到歌曲的任意时候进行识别),又怎么能做到呢?毕竟,我们只能简单地录下歌曲的末尾旋律(After all, we could just as easily have recorded the final chords of the song)。
在查询过程中,我发现一些很有意思的东西,因为我们有下面一些数据:
- 录音的哈希。 -->待匹配的数据样本的哈希值
- 可能的匹配点的哈希。-->和1匹配的哈希值(数据库里可能找到多个)
- 可能的匹配点的歌曲ID。-->和1匹配的哈希值(数据库里可能找到多个)对应的歌曲ID
- 录音中的当前时间。-->和1对应的样本时间点(处于聆听了X秒里的哪个位置)
- 可能的匹配点的哈希对应的时间。-->和1匹配的哈希值(数据库里可能找到多个)对应的时间点(建立索引数据库的时候应该知道位于歌曲的哪个位置)
现在我们可以用哈希匹配的时间(例如1352行)减去我们录音中的当前时间(例如34行),把这个差值和歌曲ID存储在一起。有了这个偏移,就能告诉我们它可能位于歌曲的哪个位置。
当我们过一遍所有的录音数据的哈希,我们就得到很多的歌曲ID和偏移量。
很酷的是,当你有了足够多的匹配偏移的哈希的时候,你就能找到你的歌曲。
结果
例如,我们聆听The Kooks – Match Box 20秒,这是我程序的输出:
Start matching song...
Top 20 matches:
01: 08_the_kooks_-_match_box.mp3 with 16 matches.
02: 04 Racoon - Smoothly.mp3 with 8 matches.
03: 05 R?yksopp - Poor Leno.mp3 with 7 matches.
04: 07_athlete_-_yesterday_threw_everyting_a_me.mp3 with 7 matches.
05: Flogging Molly - WMH - Dont Let Me Dia Still Wonderin.mp3 with 7 matches.
06: coldplay - 04 - sparks.mp3 with 7 matches.
07: Coldplay - Help Is Round The Corner (yellow b-side).mp3 with 7 matches.
08: the arcade fire - 09 - rebellion (lies).mp3 with 7 matches.
09: 01-coldplay-_clocks.mp3 with 6 matches.
10: 02 Scared Tonight.mp3 with 6 matches.
11: 02-radiohead-pyramid_song-ksi.mp3 with 6 matches.
12: 03 Shadows Fall.mp3 with 6 matches.
13: 04 R?yksopp - In Space.mp3 with 6 matches.
14: 04 Track04.mp3 with 6 matches.
15: 05 - Dress Up In You.mp3 with 6 matches.
16: 05 Supergrass - Can't Get Up.mp3 with 6 matches.
17: 05 Track05.mp3 with 6 matches.
18: 05The Fox In The Snow.mp3 with 6 matches.
19: 05_athlete_-_wires.mp3 with 6 matches.
20: 06 Racoon - Feel Like Flying.mp3 with 6 matches.
Matching took: 259 ms
Final prediction: 08_the_kooks_-_match_box.mp3.song with 16 matches.
再一次感觉就像是魔法一样:)
现在,代码还处于不能发布的状态,它工作得还不是很完美。这仅是一个周末hack,更像是个概念版或者说是算法研究。或许,有足够多的人问起的话,我会整理好代码并且在某处发布。
更新:
Shazam专利律师给我发了邮件阻止我释出代码并且要求移除这篇博文,可以在这阅读这个故事:here