AC自动机概述

转自:http://blog.csdn.net/mobius_strip/article/details/22549517#t7

AC自动机总结

0.引言：

      由于大连现场赛的一道 AC自动机+ DP的题目(zoj3545 Rescue the Rabbit)被小媛同学推荐看 AC自动机。经过一段时间的努力，终于把 shǎ崽神牛的 AC自动机专辑题目 AK(其实还差那个高中题。。囧。。不让做)。

      特别感谢：shǎ崽神牛，并附以链接：

       http://www.notonlysuccess.com/?p=607

      这一篇是关于AC自动机的英文资料，讲的比较详细，可以仔细阅读：

       http://www.cs.uku.fi/~kilpelai/BSA05/lectures/slides04.pdf

      在此仅作为自我总结，供大家参考，如果大家发现那里理解的不到位，阐述的不清楚，还请大家指出。

1.KMP算法：

      如果，真的要写关于KMP的东西，我觉得一篇文章都可能写不下。这里，只是作为AC自动机的基础，讲解一下线性的字符串匹配。（这里就不提及优化了）

      a. 传统字符串的匹配和KMP：

      对于字符串S = ”abcabcabdabba”，T = ”abcabd”，如果用T去匹配S下划线部分是当前已经匹配好的前缀，当c和d不匹配时：

            S：abcabcabdabba
            T：abcabd

      传统的算法是将T串向后移动一个单位，然后重新匹配。如果利用KMP算法则直接将T向后移动3位，即：

            S：abc ab cabdabba
            T：        ab cabd

      其中，下划线部分的ab是T和S已经匹配好的部分。

      b. next数组（函数）：

      next数组就是上面后移的关键，它用来计算当前字符串匹配失败时，T的指针向前移动的位置（这就等效于将T后移）。

      那么，为什么T利用next跳转指针是正确的，而next又是怎么求的呢。

      next[i]其实记录的就是以i为结束位置的串的后缀，和T的前缀的最大匹配长度。如下图：

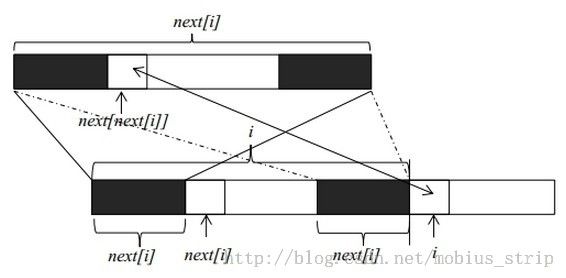
            这个图片，非常完美的揭示了KMP的实质，T的前next[i]个元素和T[i]前面的next[i]个元素是相同的。

       c. next数组（函数）的计算：

       上面的图片，也揭示了next数组的计算过程，观察图片我们会发现，其实next数组将所记录的前缀串，具有递归的属性。每个next[k]长度的黑色部分就是和下面的T [0..k-1]相同的子结构，利用递推关系就可以求解next[i]。 

       因此，如果T[i] = T[next[i]]，那么next[i+1] = next[i]+1；相反T[i] ≠ T[next[i]]，那么需要比较next[next[i]]长度的字串，即T[i]和T[next[i]]比较，一直递归到开始位置，或者一个T[i] = T[next[..next[i]..]]的状态，则next[i+1] = next[..next[i]..]+1。

 void getnext( T )
 {
     next[0] = 0;
     int i = 0,j = 1;
     while ( i < T.length ) {
         if ( T[i] == T[j] ) {
             i ++; j ++;
             next[i] = j;
         }else j = next[j];
     }
 }

     d. KMP匹配：

     对串S和T匹配，如果当前字母匹配失败，则T对应当前位置，调回到对应的next位置。

 void KMP( S，T )
 {
     int i = 0,j = 0;
     while ( i < length(T) ) {
         if ( S[i] == T[j] ) {
             i ++; j ++;
         }else j = next[j];
     }
 }

      上面是KMP算法的运行过程，是不是觉得和next的求解过程很相似呢，其实next的求解过程就是，T[0..length(T)]和T[1..length(T)]的匹配。

2.多字符串匹配问题和Trie（字典树）：

      对于多字符串匹配问题，我们一般会用hash（散列表）或者Trie（字典树）储存。

      a.hash：

      将字符串利用hash函数映射到对应的hash值，然后将字符串插入对应函数值点的储存空间。（这里不关于hash函数的选择和具体实现方式。）

      b.Trie：

      这是一个树，输的节点有|{字符集}|个指针，如果一个单词对应的字母的x后面有字母y，那么他的y指针就指向一个新的节点。

                     
            上图是一个集合{he，hers，his，she}构成的字典树。

      c.字典树的定义：

      字典树的节点如下面，数据分为两部分；一部分是指针数组，用来指向单词的下一个字母；另一部分是数据域，存储单词结尾的标记、单词计数、或者是字符串之间映射的对应串。

 typedef struct node {
     type save;
     node* next[LETTE_SIZE];
 }tnode;

      d.新单词的插入：

      从根节点开始查找，如果单词当前字母指针不空，则沿着这个指针查找；如果为空，则插入新的节点，沿着该节点方向查找。

 void insert( char* word, int l, type data )
 {
     tnode* now = root;
     for ( int i = 0 ; i < l ; ++ i ) {
         if ( !now->next[word[i]-'a'] )
             now->next[word[i]-'a'] = newnode();
         now = now->next[word[i]-'a'];
     }Deal(now->save, data);//处理相应操作
 }

      新节点的插入：每次插入的新节点，初始化所有指针和数据域初始为空。

 tnode* newnode()
 {
     for ( int i = 0 ; i < 26 ; ++ i )
         dict[size].next[i] = NULL;
     dict[size].word = NULL;
     return &dict[size ++];
 }

e.单词查询：

      返回对应单词结束位置节点的save即可。

 type query( char* word, int l )
 {
     tnode* now = root;
     for ( int i = 0 ; i < l ; ++ i ) {
         if ( !now->next[word[i]-'a'] )
             return false;
         now = now->next[word[i]-'a'];
     }return now->save;
 }

3.AC自动机的介绍：

      在此认为大家已经有了 KMP算法以及Trie（字典树）的基础（如果，上面的讲述不够详细，还请查看相关资料）。AC自动机可以理解为 KMP算法的多模式串形式扩展。
那么什么是 AC自动机呢，通俗的说就是Trie的每个节点加上了一个fail指针，fail指针指向当前匹配失败的跳转位置，这就类似于KMP的next数组。

4.AC自动机的构造：

       既然我们知道了 AC自动机是用来做什么的，那么我们就来说一说怎么在 Trie上构造 AC自动机。

       首先，我们看一下条转时的条件，如同 KMP算法一样， AC自动机在匹配时如果当前字符匹配失败，那么利用fail指针进行跳转。由此可知如果跳转，跳转到的串的前缀，必为跳转前的模式串的后缀。由此可知，跳转的新位置的深度一定小于跳之前的节点。所以我们可以利用 bfs在 Trie上面进行 fail指针的求解。

      下面，是具体的构造过程（和KMP是一样的）。首先 root节点的fail定义为空，然后每个节点的fail都取决自己的父节点的fail指针，从父节点的fail出发，直到找到存在这个字符为边的节点（向回递归），将他的孩子赋值给寻找节点。如果找不到就指向根节点，具体参照代码：

 setfail()
 {
     Q[0] = root;
     root->fail = NULL;
     for ( int move = 0,save = 1 ; move < save ; ++ move ) {//利用bfs求解
         tnode* now = Q[move];
         for ( int i = 0 ; i < dictsize ; ++ i )
             if ( now->next[i] ) {
             tnode* p = now->fail;//从父节点的fail节点开始
             while ( p && !p->next[i] ) p = p->fail;//寻找本节点的fail节点
             now->next[i]->fail = p?p->next[i]:root;//不存在fail赋值为root
             Q[save ++] = now->next[i];
         }
     }
 }

      在前面的Trie建立了fail指针（虚线）{其实，这两个图片上的字符应该是在边上的，偷懒了，网上找的图片，有时间回来自己做一下}

4.多串匹配：

      既然已经构造好 AC自动机，下面就是写出他的最常见的操作，多串匹配。其实匹配过程很简单，利用Trie匹配字符串，如果失败利用fail指针找到下次匹配的位置即可。具体参照代码：

 query( char* line )
 {
     tnode* now = root;
     for ( int i = 0 ; line[i] ; ++ i ) {
         int index = ID( line[i] );//取得字符对应的边的编号
         while ( now && !now->next[index] ) now = now->fail;//如果不能匹配，寻找fail指向的节点
         now = now?now->next[index]:root;//失败时返回root，否则返回节点
         for ( tnode* p = now ; p ; p = p->fail )
             判断匹配
     }
 }

5.对于 AC自动机的改进：

      通过匹配的过程我们可以看出，fail是用来寻找下次跳转的位置的，跳转时的 next一定是为空的。那么我们为什么不用这些 next指针直接指向下一个跳转节点呢，那样的话，匹配时每次去 next指针的对象即可。这个被称作Trie图，具体参照代码：

 setfail()
 {
     Q[0] = root;
     root->fail = NULL;
     for ( int move = 0,save = 1 ; move < save ; ++ move ) {
         tnode* now = Q[move];
         for ( int i = 0 ; i < dictsize ; ++ i )
         if ( now->next[i] ) {
             tnode* p = now->fail;
             while ( p && !p->next[i] ) p = p->fail;
             now->next[i]->fail = p?p->next[i]:root;
             Q[save ++] = now->next[i];
         }else now->next[i] = now!=root?now->fail->next[i]:root;//其实只多了这一句
     }
 }

6.从自动机的角度理解：

      自动机可以理解成一个有向图，图中的每个节点都代表一个状态，边上对应的是识别的字符，那么每次识别一个字符就会发生一个状态转向另一个状态。有一个初始状态（root），很多个结束状态（Trie中被标记的点）。

      那么我们的匹配过程就是从 root状态出发，利用串的字符寻找下一个状态，每走一步就吃掉一个字符，如果发现到达标记状态则匹配成功。

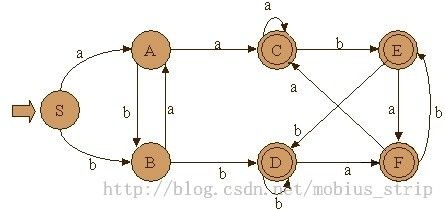
      这是一个自动机的示例，其中箭头指向的是起始状态（S），双圈的代表结束状态（C,D,E,F）

7.时间复杂度分析：

      对于Trie的匹配来说时间复杂性为：O(max(L(Pi))L(T))其中L串的长度函数，P是模式串，T是目标串。

      对于 AC自动机来说时间复杂性为：O(L(T)+max(L(Pi))+m)气质m是模式串的数量。

      对于 Trie 图 来说时间复杂性为：O(L(T))在此的时间复杂性都是指匹配的复杂度。

      对于构造的代价是 O(sum(L(Pi)))其中sum是求和函数。

8.题目分析：

      下面对于近期所做的 AC自动机的题目加以分类总结

      a.模式匹配：这类问题一般都是统计目标串中模式串的个数。下面是oj中的题目编号，和说明：

            hdu1686 Oulipo： 寻找模式串的出现次数，可以重复及覆盖，直接求解
            hdu2087 剪花布条： 同上
            hdu2222 Keywords Search： 同上
            hdu2896 病毒侵袭： 同上
            hdu3065 病毒侵袭持续中： 同上，不过要注意非法字符直接返回root，否则会RE
            hdu3336 Count thestring： 同上上
            zoj3228 Searching the String： 同上，不过不允许覆盖，记录每个状态的最晚结束位置即可
            zoj3430 Detect the Virus： 同上上，统计很简单，主要是编码有点纠结

      b.字符串统计：这类题目一般都是求解某种串个数，可先求解状态转移矩阵然后利用矩阵乘法或 DP求解

            poj2778 DNA Sequence： 求解不包含某些子串的串的个数,利用AC自动机构造转移矩阵,然后利用矩阵乘法求解路径个数
            hdu2243 考研路茫茫——单词情结：上题的升级版，做法一样，由于长度不定最后要利用快速幂和，有点纠结
            zoj1540 Censored!： 题目和上面的类似，不过状态过多不宜使用矩阵乘法，所以利用 DP求解
            hdu2825 Wireless Password： 统计关键字不少于k的串的个数，并且每个只用一次，先利用状态压缩 DP统计 

      c.字符串构造（AC自动机+DP）：其实本组和上一组基本相同，不过都是求最优解，所以单独拿出来了，而且没什么共同点

            zoj3013 Word Segmenting： 其实这个题目本来是用字典树写的,学了AC自动机之后就优化了一下,求解单词覆盖的最小失败次数
            poj3691 DNA repair： 求解将目标串取除某些串的最少操作,改变合法状态时如果对应不同则+1,否则不变;非法则不转移
            zoj3545 Rescue the Rabbit： 这就是万恶之源了,AC自动机就是为了他学的,构造最优串,用状态压缩DP记录转移状态,最后求解
            hdu2296 Ring： 构造一个串使其权值最大长度最小,而且要字典序最小。有点纠结,DP长度短的优先,然后字典序
            hdu3341 Lost's revenge： 传说中的RE神题,由于状态计算错误,导致RE2次,其实就是DP,不过要先将状态分解在拼装
            zoj3190 Resource Archiver： 本次学习的收尾题目,传说中的神题,要先构造AC自动机,然后利用最短路优化将问题转化为TSP问题

9.结束语：

      AC自动机的总结到此结束，不久后还会更新，如果那里有错还请指出。

      最后给出本人的 AC自动机的模板，和上面题目的更加详细的题解和代码，请在本空间搜索即可。

 /*
     AC自动机模板：针对具体问题需要对 query和 makeID操作行修改。
     进行了状态合并（如果一个串是另一个串的字串则值域可以合并），并且转化为 Tire图，
     一般情况下不再使用 fail指针，而是直接使用 next指针。
     如果构造某种要求的串，可构造出不包含关键字的状态转移矩阵，然后利用矩阵乘法或 DP求解。
 */

 /* AC_DFA define */
 #define nodesize 100001        //节点个数
 #define dictsize 26            //字符集大小

 typedef struct node1
 {
     int    flag;            //值域
     int    code;            //状态域
     node1* fail;
     node1* next[dictsize];
 }tnode;
 tnode  dict[nodesize+1];
 tnode* Q[nodesize+1];
 int    ID[256];

 class AC_DFA
 {
     private:
         int    size;
         tnode* root;
     public:
         AC_DFA() {
             makeID();
             memset( dict, 0, sizeof( dict ) );
             root=NULL; size=0; root=newnode();
         }
         void makeID() {
             for ( int i = 0 ; i < 26 ; ++ i )
                 ID['a'+i] = i;
         }
         void init() {
             memset( dict, 0, sizeof( dict ) );
             root=NULL; size=0; root=newnode();
         }
         tnode* newnode() {
             dict[size].code = size;
             dict[size].fail = root;
             return &dict[ size ++ ];
         }
         void insert( char* word, int l ) {
             tnode* now = root;
             for ( int i = 0 ; i < l ; ++ i ) {
                 if ( !now->next[ID[word[i]]] )
                     now->next[ID[word[i]]] = newnode();
                 now = now->next[ID[word[i]]];
             }now->flag = 1;//now->flag ++ 用于统计
         }
         void setfail() {
             Q[0] = root; root->fail = NULL;
             for ( int move = 0,save = 1 ; move < save ; ++ move ) {
                 tnode* now = Q[move];
                 for ( int i = 0 ; i < dictsize ; ++ i )
                     if ( now->next[i] ) {
                         tnode* p = now->fail;
                         while ( p && !p->next[i] ) p = p->fail;
                         now->next[i]->fail  = p?p->next[i]:root;
                         //now->next[i]->flag += now->next[i]->fail->flag;//状态合并，不能计数
                         Q[save ++] = now->next[i];
                     }else now->next[i] = now==root?root:now->fail->next[i];//构建 Trie图
             }
         }
         int query( char* line, int L ) {//统计字串出现个数，可重复及交叉
             int sum = 0;
             tnode *temp,*now = root;
             for ( int i = 0 ; i < L ; ++ i ) {
                 now = now->next[ID[line[i]]];
                 temp = now;
                 while (temp && temp->flag) {
                     sum += temp->flag;
                     temp = temp->fail;
                     //temp->flag = 0 用于统计时相同的单词只计数一次
                 }
             }
             return sum;
         }
 };
 /* AC_DFA  end */

      这篇文章写于2011年10月，为了增加可读性，本次更新加入了KMP和Tire的概述。

                                                                                             ——————by  zzu_xiaobai 2014-03-30

      感谢J_Sure指出模版中的bug，已修正统计部分。——————2014-12-21

      感谢_rebort指出KMP算法描述中next的描述错误。——————2015-08-18

      如果有什么建议，还请大家积极留言，以便下次整理修正。