第二章 算法
什么是算法?1+1=2算不算算法?严格讲算法不分难易,能解决数学问题的方法都叫算法。
哈,下面让我们看一下严格的定义吧:算法是解决特定问题求解步骤的描述,在计算机中表现为指令的有限序列,并且每条指令表示一个或者多个操作。
一、数据结构和算法的关系
数据结构和算法什么关系?这不是介绍数据结构的文章吗,为什么扯到算法了呢?
如果上一章你看了的话,应该会记得一个公式:程序设计=数据结构+算法。(牛人就是牛人,一个公式就说明了所有的关系)通俗地来讲这个数据结构和算法的关系就像梁山伯和祝英台、罗密欧和朱丽叶的关系。只谈数据结构和只谈算法是没有意义的,它们俩在一起才能碰撞出智慧的火花!
二、算法优劣的比较
上过小学的童鞋(废话)应该都遇到过这样一个经典的问题吧:1+2+3+...+100,要解决这样一个问题,程序改怎么写?凭你的智商相信这个难不住你吧:
public class Add {
public static void main(String args[]) {
int sum = 0;
int n = 100;
for (int i = 1; i <= 100; i++) {
sum = sum + i;
}
System.out.println(sum);
}
}
最近在用Java,就用Java写了啊,算法其实是超脱语言的,什么语言都能展现。
这个程序其实是不经过思考写出来的程序,当然计算机的运行速度很快我们感觉不到,要让你用笔算估计你就崩溃了。
话说还有没有更省时的算法呢?上过高中的同学都应该学过等差数列吧,这其实就是一个最简单的等差数列求和,当然我们有求和公式啦!一百个加法换成一个乘法,是不是很伟大的转换?节省了大量的时间。
其实我们所要追求的境界就是在能用更好的方法解决问题,而不是仅仅只是解决问题这么简单,这就是算法的魅力。
三、算法特性
算法具有五个基本特性:输入、输出、有穷性、确定性和可行性。
输入输出:算法具有零个或多个输入,有一个或多个输出。(也就是说可以没有输入但是必有有输出)
有穷性:指算法在执行有限个步骤之后,自动结束而不会出现无限循环,并且每个步骤在可接受的时间内完成。
确定性:算法的每一个步骤都有确定的含义,不会出现二义性。
可行性:算法的每一步都必须是可行的,也就是说每一步都能够通过执行有限次数完成。
四、算法设计的要求
1.正确性:算法的正确性是指算法至少应该有输入、输出金额加工处理无歧义性、能正确反映问题的需求、能够得到问题的正确答案。
2.可读性:算法设计的另一个目的是为了便于阅读、理解和交流。
3.健壮性:当输入不合法的数据时,算法也能进行相关处理,而不是产生程序崩溃、异常退出等。
4.时间效率高和存储量低。
五、算法效率的度量方法
凡事讲求证据,你说别人的算法效率低,总的拿出来标准吧,这个标准也就是度量的方法,才能让别人心服口服。
1.事后统计方法:这种方法主要是通过设计好的测试程序和数据,利用计算机计时器对不同的算法编制的程序的运行时间进行比较,从而确定算法效率的高低。(想法很简单,实施起来不容易,也缺乏公信力,不予采纳)
2.事前分析估算方法:在计算机程序编制前,依据统计方法对算法进行估算。
第二节讨论的问题可以量化优劣了:
第一种算法执行了2n+3次,第二种算法执行了3次。假如n很大的话,这执行时间可就不是一个数量级了吧。所以说研究算法很大程序上是在研究执行效率上面。
六、算法时间复杂度
1.定义:在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。算法的时间复杂度,也就是算法的时间量度,记作:T(n)=O(f(n))。它表示随着问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐进时间复杂度,简称时间复杂度。
2.推导大O阶方法
推导大O阶:
1.用常数1取代运行时间中的所有加法常数。O(3)=O(1)
2.在修改后的运行次数函数中,只保留最高项。O(n^2+n)=O(n^2)
3.若果最高阶存在且不是1,则除去与这个项相乘的常数。得到的结果就是大O阶。O(2n^2)=O(n^2)
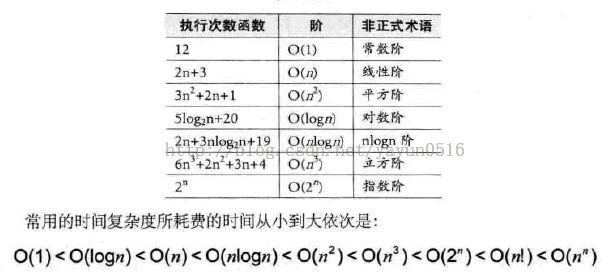
下表介绍常见的时间复杂度: