优先队列——左式堆的实现

零路径长度(null path length, NPL)，NPL(X)定义为从X到一个没有两个儿子的节点的最短路径的长。因此具有0个或1个儿子的节点的NPL为0，而NPL(NULL) = -1。

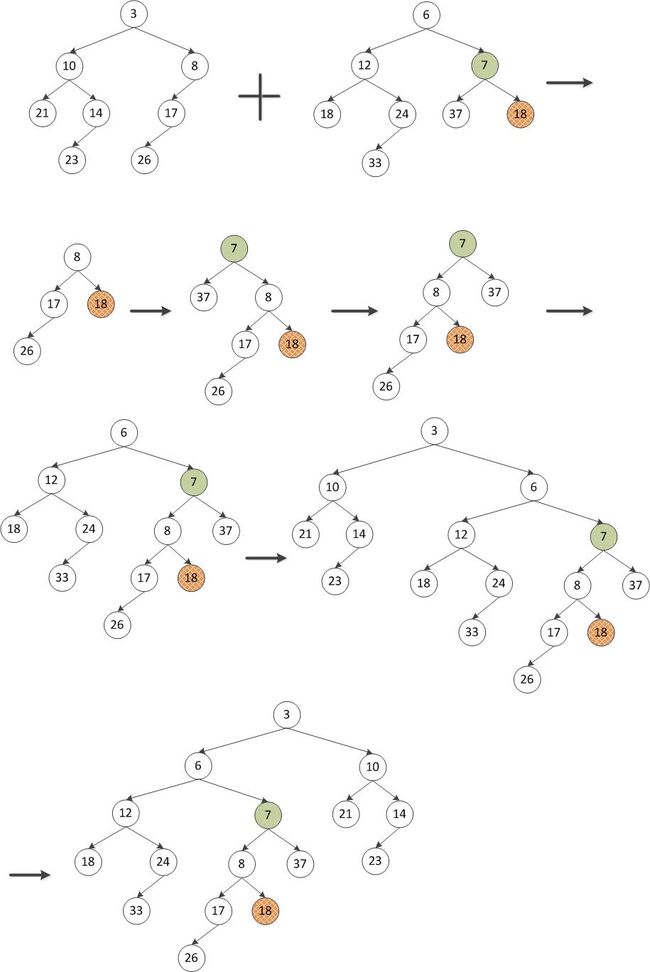
左式堆性质是：对于队中的每一个节点X，左儿子的零路径长至少与右儿子的零路径长一样大。左式堆与二叉堆具有相同的堆序性质，惟一的区别在于左式堆不是理想平衡的，而实际上是趋于非常不平衡的。左式堆的基本操作是合并。其中，插入只是合并的特殊情形，因为我们可以把插入看成是单个节点堆与一个大的堆的Merge。注意，最小的元素在根节点。

如下图左式堆合并

fatal.h错误处理

#include <stdio.h>
#include <stdlib.h>

#define Error(str) FatalError(str)
#define FatalError(str) fprintf(stderr, "%s\n", str),exit(1)

leftheap.h左式堆函数声明

typedef int ElementType;

#ifndef LEFTHEAP_H
#define LEFTHEAP_H

struct TreeNode
{
	ElementType Element;
	struct TreeNode *Left;
	struct TreeNode *Right;
	int Npl;//零路径长
};

typedef struct TreeNode *PriorityQueue;

PriorityQueue Initialize(void);//初始化堆
ElementType FindMin(PriorityQueue H);//查找最小值
int IsEmpty(PriorityQueue H);//判断是否为空
PriorityQueue Merge(PriorityQueue H1, PriorityQueue H2);//合并两个左式堆
PriorityQueue Insert(ElementType X, PriorityQueue H);//插入节点，即单节点与堆合并
PriorityQueue DeleteMin(PriorityQueue H);//删除最小值

#endif

leftheap.c左式堆具体实现

#include "fatal.h"
#include "leftheap.h"
#include <stdlib.h>

PriorityQueue Initialize(void)
{
	return NULL;
}
static PriorityQueue Merge1(PriorityQueue H1, PriorityQueue H2);

PriorityQueue Merge(PriorityQueue H1, PriorityQueue H2)
{
	if(H1 == NULL)
		return H2;
	if(H2 == NULL)
		return H1;
	if(H1->Element < H2->Element)
		return Merge1(H1, H2);
	else
		return Merge1(H2, H1);
}

void SwapChildren(PriorityQueue H)
{
	PriorityQueue Tmp;

	Tmp = H->Left;
	H->Left = H->Right;
	H->Right = Tmp;
}

static PriorityQueue Merge1(PriorityQueue H1, PriorityQueue H2)
{
	if(H1->Left == NULL)
		H1->Left = H2;
	else
	{
		H1->Right = Merge(H1->Right, H2);
		if(H1->Left->Npl < H1->Right->Npl)
			SwapChildren(H1);
		H1->Npl = H1->Right->Npl + 1;
	}

	return H1;
}

PriorityQueue Insert(ElementType X, PriorityQueue H)
{
	PriorityQueue SingleNode;

	SingleNode = (PriorityQueue)malloc(sizeof(struct TreeNode));
	if(SingleNode == NULL)
		FatalError("Out of space");
	else
	{
		SingleNode->Element = X;
		SingleNode->Npl = 0;
		H = Merge(SingleNode, H);
	}
	return H;
}

PriorityQueue DeleteMin(PriorityQueue H)
{
	PriorityQueue LeftHeap, RightHeap;

	if(IsEmpty(H))
	{
		Error("Priority queue is empty");
		return H;
	}

	LeftHeap = H->Left;
	RightHeap = H->Right;
	free(H);
	return Merge(LeftHeap, RightHeap);
}

ElementType FindMin(PriorityQueue H)
{
	if(!IsEmpty(H))
		return H->Element;
	Error("Priority queue is empty");
	return 0;
}

int IsEmpty(PriorityQueue H)
{
	return H == NULL;
}

main.c测试左式堆

#include "leftheap.h"
#include <stdio.h>
#include <stdlib.h>

#define MaxSize 5000

int main()
{
	PriorityQueue H;
	int i, j;

	H = Initialize();
	for(i = 0, j = MaxSize / 2; i < MaxSize; i++, j = (j + 17) % MaxSize)
		Insert(j, H);
	j = 0;
	while(!IsEmpty(H))
		if(FindMin(H) != j++)
			printf("Error in DeleteMin, %d\n", j);
		else
			H = DeleteMin(H);
	printf("Done...\n");
	system("Pause");
	return 0;
}